相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、分解因式:(1)、(2)、(3)、(4)、
-
2、分解因式:(1)、2a(b+c)-3(b+c);(2)、
-
3、把分解因式.
-
4、利用因式分解计算:(1)、(2)、49×20.22+52×20.22-20.22;(3)、
-
5、分解因式:(1)、ax-ay;(2)、(3)、(4)、
-
6、下列由左边到右边的式子变形,哪些是因式分解?哪些不是?为什么?(1)、(2)、(3)、
-
7、分解因式:(1)、(2)、
-
8、 如图, 连接AC, AD, BD, BE, CE, 求证

-
9、 如图, 在△ABC中, BE,CF是角平分线, 且BE, CF 相交于点G. 求证:
 (1)、(2)、
(1)、(2)、 -
10、 如图, 在△ABC 中, AD 是高, AE, BF 是角平分线, 且AE, BF 相交于点O,∠BAC=50°, ∠C=70°. 求∠DAC 和∠BOA 的度数.

-
11、 如图, 在△ABC 中,∠C=∠ABC=2∠A, BD是边AC上的高. 求∠DBC 的度数.

-
12、 如图, ∠B=42°, ∠A 比∠1小10°, ∠ACD=64°. 求证AB∥CD.

-
13、求出下列各图形中x的值.(1)、
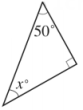 (2)、
(2)、 (3)、
(3)、
-
14、如图, 填空:
由三角形两边的和大于第三边,得AB+AD> , PD+CD>.
将不等式左边、右边分别相加,得AB+AD+PD+CD> , 即 AB+AC>.

-
15、 如图, 在△ABC中, AD, AE 分别是边BC 上的中线和高,AE=2, S△ABD =1.5. 求 BC 和DC 的长.

-
16、下列四个条件:
①在△ABC 中, ∠A, ∠B 都是锐角;
②△ABC的三个内角的度数之比是1:2:3;
③在△ABC中, ∠A-∠B=∠C;
④△ABC的三个外角的度数之比是3:4:5.
其中能确定△ABC 是直角三角形的是(只填序号).
-
17、 如图, 已知点A, B在直线a上, 点C, D, E在直线b上.以点A,B,C,D,E中的任意三点作为三角形的顶点,一共可以组成多少个三角形?分别写出这些三角形
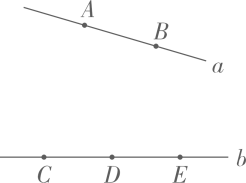
-
18、 如图, AB=BC=CD=DA=AC, 找出图中的等腰三角形和等边三角形.

-
19、 如图, 在△ABC 中, AD⊥BC, 垂足为D,∠BAC 是钝角, E 是DC 上一点, 且∠BAE 是锐角.
 (1)、图中有几个三角形?用符号表示这些三角形.(2)、找出图中的锐角三角形、直角三角形和钝角三角形.
(1)、图中有几个三角形?用符号表示这些三角形.(2)、找出图中的锐角三角形、直角三角形和钝角三角形. -
20、图中有几个三角形?用符号表示这些三角形.
