相关试卷

1、计算：

(1)、 $\frac{4 a + 4 b}{5 a b} \cdot \frac{15 a^{2} b}{a^{2} - b^{2}};$

(2)、 $\frac{x^{2} - 4 y^{2}}{x^{2} + 4 x + 4} \cdot \frac{x + 2}{3 x^{2} + 6 x y};$

(3)、 $\frac{x^{2} + 1}{x - 6} \cdot \frac{x^{2} - 36}{x^{3} + x};$

(4)、 $\frac{y^{2} - x^{2}}{5 x^{2} - 4 x y} \div \frac{x + y}{5 x - 4 y} .$

查看解析
2、计算：

(1)、 $\frac{6 a b}{5 c^{2}} \cdot \frac{10 c}{3 b};$

(2)、 $\frac{- 7 x}{3 y z} \cdot (- \frac{9 y^{2}}{x^{2}});$

(3)、 $\frac{2 m}{5 n} \div \frac{4 m^{2}}{10 n^{3}};$

(4)、 $\frac{x}{5 y} \div (- \frac{4 x^{2}}{5 y^{2}}) .$

查看解析
3、计算：

(1)、 $(\frac{- 2 x^{4} y^{2}}{3 z})^{3};$

(2)、 $(\frac{2 x}{3 y})^{2} \cdot (\frac{3 y}{4 x})^{3}$

(3)、 $(\frac{b^{2}}{a c})^{3} \div (- b^{6} c)$

(4)、 $(\frac{2 a b^{3}}{- c^{2} d})^{2} \div \frac{6 a^{4}}{b^{3}} \cdot (\frac{- 3 c}{b^{2}})^{3}$

查看解析
4、计算：

(1)、 $\frac{2 m^{2} n}{3 p q^{2}} \cdot \frac{5 p^{2} q}{4 m n^{2}} \div \frac{5 m n p}{3 q};$

(2)、 $\frac{16 - a^{2}}{a^{2} + 8 a + 16} \div \frac{a - 4}{2 a + 8} \cdot \frac{a - 2}{a + 2}$

查看解析
5、计算：

(1)、 ${(\frac{- 2 a^{2} b}{3 c})}^{2};$

(2)、 ${(\frac{a^{2} b}{- c d^{3}})}^{3} \div \frac{2 a}{d^{3}} \cdot {(\frac{c}{2 a})}^{2} .$

查看解析
6、计算 $\frac{2 x}{5 x - 3} \div \frac{3}{25 x^{2} - 9} \cdot \frac{x}{5 x + 3} .$

查看解析
7、大拖拉机m 天耕地a hm² ，小拖拉机n 天耕地bhm² ，大拖拉机的工作效率是小拖拉机工作效率的多少倍?

查看解析
8、一个水平放置的长方体容器，其容积为V，底面的长为a，宽为b，当容器内的水占容积的m时，水面的高度为多少?

查看解析
9、计算：

(1)、 $\frac{3 a - 3 b}{10 a b} \cdot \frac{25 a^{2} b^{3}}{a^{2} - b^{2}};$

(2)、 $\frac{4 y^{2} - x^{2}}{x^{2} + 2 x y + y^{2}} \div \frac{x - 2 y}{2 x^{2} + 2 x y} .$

查看解析
10、计算：

(1)、 $\frac{3 a}{4 b} \cdot \frac{16 b}{9 a^{2}};$

(2)、 $\frac{12 x y}{5 a} \div (8 x^{2} y);$

(3)、 $(- 3 x y) \div \frac{2 y^{2}}{3 x};$

(4)、 $\frac{x + y}{x - y} \cdot \frac{y - x}{x + y} .$

查看解析
11、如图，“丰收1号”小麦的试验田是边长为a m(a>1)的正方形去掉一个边长为1m的正方形蓄水池后余下的部分，“丰收2号”小麦的试验田是边长为(a-1)m的正方形，两块试验田都收获了500kg小麦.

(1)、哪种小麦的单位面积产量高?

(2)、高的单位面积产量是低的单位面积产量的多少倍?

查看解析
12、计算：

(1)、 $\frac{a^{2} - 4 a + 4}{a^{2} - 2 a + 1} \cdot \frac{a - 1}{a^{2} - 4};$

(2)、 $\frac{1}{49 - m^{2}} \div \frac{1}{m^{2} - 7 m} .$

查看解析
13、计算：

(1)、 $\frac{4 x}{3 y} \cdot \frac{y}{2 x^{3}};$

(2)、 $\frac{a b^{3}}{2 c^{2}} \div \frac{- 5 a^{2} b^{2}}{4 c d} .$

查看解析
14、如图， ∠B=∠C=90°， E是BC的中点， DE平分∠ADC . 求证： AE 平分∠DAB.(提示：过点E 作EF⊥AD，垂足为 F.)

查看解析
15、如图， AD 是△ABC的角平分线， DE⊥AB，DF⊥AC，垂足分别为E， F，连接EF，EF 与AD 相交于点G. AD 与EF 垂直吗?证明你的结论.

查看解析
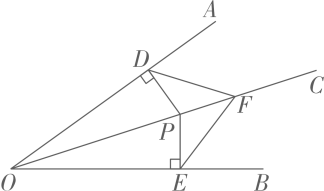
16、如图， OC 是∠AOB 的平分线， P 是OC 上的一点， PD⊥OA， PE⊥OB，垂足分别为 D， E. F 是OC上的另一点，连接DF， EF. 求证DF=EF.

查看解析
17、如图，在△ABC中，AD是它的角平分线， P 是AD 上一点， $P E ‖ A B,$ 交BC 于点E， PF∥AC，交BC于点F. 求证：点 D 到PE 和PF 的距离相等.

查看解析
18、如图，在 $R t △ A B C$ 中， $∠ C = 9 0^{\circ},$ ，在边 AC 上求作一点P，使点 P 到边 BC和边AB 的距离相等.

查看解析
19、如图， CD⊥AB， BE⊥AC，垂足分别为D， E， BE， CD 相交于点O， OB=OC. 求证∠1=∠2.

查看解析
20、如图，在△ABC 中， AB=AC， BD⊥AC， CE⊥AB，垂足分别为D， E，BD，CE 相交于点F. 求证： FA 平分∠DFE.

查看解析

上一页 854 855 856 857 858 下一页跳转