相关试卷

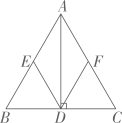
1、如图，在等边三角形 ABC 中，AD 是BC 上的高，∠BDE=∠CDF=60°，图中有哪些与 BD相等的线段?证明你的结论.

查看解析
2、画出等边三角形的三条对称轴.你能发现什么?

查看解析
3、如图， △ABC 是等边三角形，DE∥BC，分别交AB， AC 于点D， E. 求证：△ADE 是等边三角形.

查看解析
4、如图， AC和BD相交于点O，且AB∥CD，OA=OB.求证OC=OD.

查看解析
5、如图，把一张长方形的纸沿对角线折叠，重合部分是一个等腰三角形吗?为什么?

查看解析
6、如图， ∠A=36°，∠DBC=36°， ∠C=72°. 分别计算∠1， ∠2的度数，并说明图中有哪些等腰三角形.

查看解析
7、尺规作图：已知等腰三角形的底边长为a，底边上高的长为h (图 (1)，求作这个等腰三角形.

查看解析
8、求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形.
已知：如图， AD 是△ABC 的外角∠CAE 的平分线， AD∥BC.
求证： AB=AC.

查看解析
9、求证：如果三角形一条边上的中线等于这条边的一半，那么这个三角形是直角三角形.

查看解析
10、如图，在△ABC中， AB=AD=DC， ∠BAD=26°. 求∠B 和∠C的度数.

查看解析
11、如图，在下列等腰三角形中，分别求出它们的底角的度数.

(1)、

(2)、

查看解析
12、如图，在△ABC 中， AB=AC，点 D 在AC 上， BD=BC=AD. 求△ABC各角的度数.

查看解析
13、如图，分别作出 $△ P Q R$ 关于直线m （直线m 上各点的横坐标都为1）和直线n （直线n 上各点的纵坐标都为 $- 1 ）$ 对称的图形.它们的对称点的坐标之间分别有什么关系?

查看解析
14、如图，已知点A，B，C，请你再找一个点D，使A，B，C，D 四点构成一个轴对称图形.这样的点 D 有几个?

查看解析
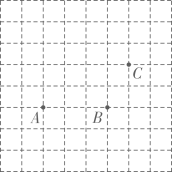
15、如图，小球起始时位于（3，0）处，沿所示的方向击球，小球运动的轨迹如图所示，用坐标描述这个运动，找出小球运动的轨迹上几个关于直线 l 对称的点.如果小球起始时位于（1，0）处，仍按原来方向击球，请你画出这时小球运动的轨迹.

查看解析
16、根据下列点的坐标的变化，判断它们进行了怎样的变化.

(1)、（-1， 3）→（--1， - 3）；

(2)、（-5， - 6）→（-5， - 1）；

(3)、（3， 4）→（-3， 4）；

(4)、（-2， 3）→（2， - 3）.

查看解析
17、如图，利用关于坐标轴对称的点的坐标的特点，分别画出△ABC 关于x轴和y 轴对称的图形.

查看解析
18、如图，以正方形 ABCD 的中心为原点建立平面直角坐标系.点A 的坐标为（1， 1），写出点B， C， D的坐标.

查看解析
19、在下列各图中的适当位置添加最少的小方格，使得到的图形关于虚线成轴对称.

查看解析
20、如图，将各图形补成关于直线l 对称的图形.

查看解析

上一页 850 851 852 853 854 下一页跳转