相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、如图所示的每幅图形中的两个图案是成轴对称的吗?如果是,指出它们的对称轴,并找出一对对称点.

-
2、如图所示的每个图形是轴对称图形吗?如果是,指出它的对称轴.

-
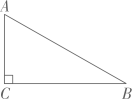
3、如图,要把一块三角形的土地均匀分给甲、乙、丙三家农户. 如果∠C=90°, ∠B=30°, 要使这三家农户所得土地的大小、形状都相同,请你试着分一分,并在图上画出来.
-
4、等腰三角形两底角的平分线相等吗?两腰上的中线呢?两腰上的高呢?证明其中的一个结论.你还能发现其他结论吗?
-
5、 如图, P, Q 是△ABC 的边BC上的两点, 并且BP=PQ=QC=AP=AQ.求∠BAC 的度数.

-
6、 如图, 在 中, , 交 BC 于点 D. 若 求BC的长.

-
7、 如图, 都是等边三角形.求证 BE=DC.

-
8、 如图, △ABC是等边三角形, E是边AC上的点, 且∠1=∠2, CD=BE.判断△ADE 的形状,并说明理由.

-
9、上午8时,一条船从海岛A 出发,以15 n mile/h的速度向正北航行,10时到达海岛B处. 从A, B 望灯塔C, 测得∠NAC=42°, ∠NBC=84°. 求海岛B 与灯塔C 的距离.

-
10、某中学的同学们设计了下面的方法检测教室的房梁是否水平:
在等腰直角三角尺斜边的中点拴一条线绳,线绳的另一端挂一个铅锤,把这块三角尺的斜边贴在房梁上,如果线绳经过三角尺的直角顶点,那么可以确定房梁是水平的.他们的方法对吗?为什么?

-
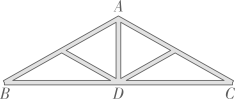
11、如图,厂房屋顶钢架外框是等腰三角形,其中AB=AC,立柱AD⊥BC,且顶角∠BAC=120°. AD 与AB有什么数量关系?
-
12、 如图, AB=AC,∠A=40°, AB 的垂直平分线MN交AC 于点D. 求∠DBC的度数.

-
13、 如图,∠A=∠B=60°, CE∥DA, CE交AB 于点E.求证: △CEB是等边三角形.

-
14、 如图, 在△ABC 中, 点 D, E 在边 BC 上, AB=AC, AD=AE. 求证 BD=CE.

-
15、如图,五角星中有五个全等的等腰三角形,它们的顶角都是 36°.求∠AMB的度数.

-
16、 如图, AD∥BC, BD平分∠ABC.求证AB=AD.

-
17、(1)、等腰三角形的一个角是110°,它的另外两个角是多少度?(2)、等腰三角形的一边长是8,周长是18,它的另外两边长是多少?
-
18、 在Rt△ABC中,∠C=90°, AB=2BC, ∠B和∠A 各是多少度?
-
19、 在 中,∠C=90°,∠B=2∠A,∠B 和∠A各是多少度? 边AB 与BC之间有什么关系?
-
20、如图是屋架设计图的一部分,点D 是斜梁AB 的中点, 立柱BC, DE 垂直于横梁AC, AB=7.4m ,∠A=30°. 求立柱BC, DE的长.
