相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、 如图, AB∥CD, ∠BAE=∠DCE=45°. 填空:
∵ AB∥CD,
.
∴ ∠1+∠2=.
∴ ∠E=.

-
2、 如图, 在△ABC中, ∠A=100°,∠1=∠2, ∠3=∠4. 求x的值.
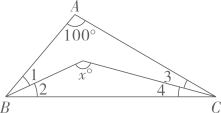
-
3、 如图, 在△ABC 中, D 是边AB上一点, E 是边AC 上一点, BE, CD 相交于点F, ∠A=62°, ∠ACD=35°, ∠ABE=20°. 求∠BDC和∠BFD 的度数.
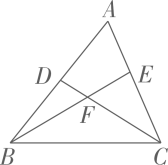
-
4、如图,B 处在A 处的南偏西45°方向,C 处在A 处的南偏东15°方向,C 处在B 处的北偏东 80°方向.求∠ACB 的度数.
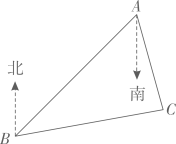
-
5、 如图, AB∥CD, AE与CD相交于点O, ∠A=45°,∠C=∠E. 求∠C 的度数.
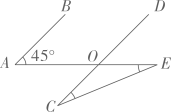
-
6、 如图, AB∥CD, ∠A=40°, ∠D=45°. 求∠1和∠2的度数.
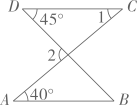
-
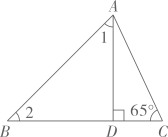
7、如图, 在 中, 垂足为 D, 求 的度数.
-
8、 在 中, 比 大 比 大 求 各内角的度数.
-
9、(1)、一个三角形最多有几个直角?为什么?(2)、一个三角形最多有几个钝角?为什么?(3)、直角三角形的外角可以是锐角吗?为什么?
-
10、求出下列各图形中x的值:(1)、
 (2)、
(2)、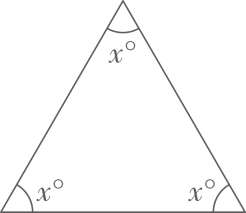 (3)、
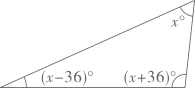
(3)、 (4)、
(4)、
-
11、 说出下列各图形中∠1和∠2的度数:(1)、
 (2)、
(2)、 (3)、
(3)、 (4)、
(4)、 (5)、
(5)、 (6)、
(6)、
-
12、如图 13.3-9, ∠BAE, ∠CBF, ∠ACD 样,推论可以作为进一是△ABC 的三个外角,它们的和是多少?

-
13、 如图, 在△ABC 中,∠C=90°, 点 D, E分别在边AB,AC上, 且∠1=∠2, △ADE 是直角三角形吗? 为什么?

-
14、 如图, 在△ABC 中, ∠ACB=90°, CD⊥AB, 垂足为 D.∠ACD 与∠B 有什么关系?为什么?

-
15、如图13.3-6,∠C=∠D=90°, AD, BC 相交于点E. 比较∠CAE与∠DBE 的大小.

-
16、 如图, 在△ABC 中, ∠A=40°, 求∠B+∠C+∠ADE+∠AED的度数.

-
17、如图,从A 处观测C 处的仰角∠CAD=30°,从B 处观测C 处的仰角∠CBD=45°.从C 处观测A, B 两处的视角∠ACB 是多少度?

-
18、如图是A, B, C三岛的平面图,C岛在A 岛的北偏东50°方向,B 岛在A 岛的北偏东80°方向,C 岛在B 岛的北偏西40°方向.从 B 岛看A,C 两岛的视角∠ABC 是多少度?从C 岛看A, B 两岛的视角∠ACB 呢?

-
19、如图, 在△ABC 中, ∠BAC=40°, ∠B =75°, AD 是△ABC 的角平分线. 求∠ADB 的度数.

-
20、 如图, 在△ABC 中, 边AB, BC 的垂直平分线相交于点 P.
 (1)、求证:PA=PB=PC.(2)、点P 是否也在边AC 的垂直平分线上?由此你还能得出什么结论?
(1)、求证:PA=PB=PC.(2)、点P 是否也在边AC 的垂直平分线上?由此你还能得出什么结论?