相关试卷

1、先化简，再求值： $a^{2} b - 4 a b^{2} + 1 - 2 (a^{2} b - 2 a b^{2} - 1)$ ，其中 $a = \sqrt{3}$ ， $b = - 1$ ．

查看解析
2、解方程：

(1)、 $2 x - 3 = 4 + 5 x$ ；

(2)、 $\frac{x - 4}{4} = 1 - \frac{2 x - 1}{2}$ ．

查看解析
3、计算：

(1)、 $- 5 + 18 \times (\frac{1}{3} - \frac{1}{2})$ ；

(2)、 $- 3^{2} \times \sqrt{\frac{1}{9}} + \sqrt[3]{- 8} - |- 4|$ ．

查看解析
4、如图，用火柴棒按照一定规律摆出一组图形，照此规律摆下去，第 $n + 1$ 个图形比第n个图形多出的火柴棒根数是（用含n的式子表示，n为正整数）．

查看解析
5、若 $\sqrt{x + 8} + | y + 2 | = 0$ ，则 $x y$ 的值为．

查看解析
6、已知关于x的方程 $2 (x - 2) = x - 3 a$ 的解为 $x = 3$ ，则 $a$ 的值为．

查看解析
7、如图，小明和小红看到建筑工人砌墙时经常先在两端立桩、拉线，然后沿着线砌出笔直的墙．小明认为依据是两点之间，线段最短；小红认为依据是两点确定一条直线，你认为的说法正确．（填“小明”或“小红”）

查看解析
8、如图，将①和②两张正方形纸片按图示两种方式放置在同一个长方形中，正方形①边长为 $a$ ，正方形②边长为 $b$ ，长方形长为 $c$ ，宽为 $d$ ，已知图 $1$ 的阴影部分周长为 $10$ ，若要求图 $2$ 阴影部分的周长，只需要知道（）

A、a B、b C、c D、d

查看解析
9、直线 $l$ 上有A，B，C三点， $A B = 4 cm$ ， $B C = 3 A B$ ，则 $A C$ 的长度为（）

A、 $8cm$ B、 $12cm$ C、 $8cm$ 或 $16cm$ D、 $12cm$ 或 $16cm$

查看解析
10、我国明代数学读本《算法统宗》中有一道题：“隔墙听得客分银，不知人数不知银，六两分之多三两，八两分之少四两，问客、银各几许？”其题意为：客人一起分银子，若每人6两，还剩3两；若每人8两，还差4两．问客人共有几人，银子共有几两？若设客人共有x人，则可列方程为（）

A、 $6 x + 3 = 8 x - 4$ B、 $6 x - 3 = 8 x + 4$ C、 $\frac{x - 3}{6} = \frac{x + 4}{8}$ D、 $\frac{x + 3}{6} = \frac{x - 4}{8}$

查看解析
11、已知 $a < \sqrt{17} < b$ ， $a$ 和 $b$ 为相邻的整数，则 $a + b$ 的值为（）

A、8 B、9 C、10 D、11

查看解析
12、如果 $m = n$ ，那么下列等式一定成立的是（）

A、 $m + 4 = n - 3$ B、 $4 - m = n - 4$ C、 $\frac{m}{c} = \frac{n}{c}$ D、 $a m = a n$

查看解析
13、下列计算结果正确的是（）

A、 $2 x + 3 y = 5 x y$ B、 $3 a^{2} - a^{2} = 2$ C、 $5 x^{2} y - 5 y x^{2} = 0$ D、 $- 4 m + m = - 5 m$

查看解析
14、单项式 $- a^{2} b c^{3}$ 的系数和次数分别是（）

A、0，3 B、1，3 C、 $- 1$ ， 5 D、 $- 1$ ， 6

查看解析
15、在实数 $3.14159265$ ， $- \sqrt{5}$ ， $\frac{2}{7}$ ， $\sqrt[3]{64}$ 中，属于无理数的是（）

A、 $3.14159265$ B、 $- \sqrt{5}$ C、 $\frac{2}{7}$ D、 $\sqrt[3]{64}$

查看解析
16、省文化广电旅游厅数智通平台节假日数据显示，2024年国庆黄金周，台州市共接待游客约3312000人次，数据3312000用科学记数法表示为（）

A、 $3312 \times 10^{3}$ B、 $0.3312 \times 10^{7}$ C、 $3.312 \times 10^{6}$ D、 $3.312 \times 10^{7}$

查看解析
17、如图， $a$ ， $b$ ， $c$ ， $d$ ， $e$ ， $f$ 均为有理数，图中各行，各列及两条对角线上三个数的和都相等，则 $a - b + c - d + e - f$ 的值为( )
4
$- 1$
$a$
$b$
3
$c$
$d$
$e$
$f$

A、1 B、 $- 3$ C、7 D、8

查看解析
18、如图，在四边形 $A B C D$ 中， $A D ∥ B C$ ， $E$ 为对角线 $B D$ 上一点， $∠ A + ∠ C E D = 180 °$ ，且 $A D = B E$ ．

(1)、求证： $△ A B D ≌ △ E C B$ ．

(2)、若 $B C = 15$ ， $D E = 9$ ，求 $A D$ 的长．

查看解析
19、如图，将线段 $A B$ 平移至 $C D$ ，则 $m + n$ 的值为（）

A、2 B、2.5 C、3 D、3.5

查看解析
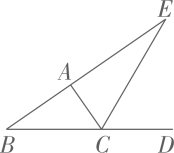
20、如图， CE 是△ABC 的外角∠ACD 的平分线，且 CE 交 BA 的延长线于点E. 求证∠BAC=∠B+2∠E.

查看解析

上一页 846 847 848 849 850 下一页跳转

4	$- 1$	$a$
$b$	3	$c$
$d$	$e$	$f$