相关试卷

1、将一元二次方程 $x^{2} - 2 x - 3 = 0$ 化成 ${(x + a)}^{2} = b$ （ $a$ ， $b$ 为常数）的形式，下列方程正确的是（）

A、 ${(x - 1)}^{2} = 2$ B、 ${(x + 1)}^{2} = 2$ C、 ${(x - 1)}^{2} = 4$ D、 ${(x + 1)}^{2} = 4$

查看解析
2、已知反比例函数 $y = - \frac{8}{x}$ 的图象经过点 $P (2, a)$ ，则 $a$ 等于（）

A、4 B、 $- 4$ C、16 D、 $- 16$

查看解析
3、方程 $(x + 1) (x - 3) = 0$ 的解为．

查看解析
4、如图1，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $B C = 3$ ， $A C = 6$ ， $D$ 为射线 $A B$ 上一点，连接 $C D$ ，过 $C D$ 作 $C E ⊥ C D$ ，且 $\frac{C D}{C E} = \frac{1}{2}$ ，连接 $D E$ 、 $A E$ ．

(1)、求证： $△ B C D ∽ △ A C E$ ；

(2)、如图2，若 $D$ 在线段 $A B$ 上，连接 $B E$ ， $M$ 为 $B E$ 中点， $N$ 为 $A D$ 中点，连接 $M N$ ，求证： $A E = \frac{4 \sqrt{5}}{5} M N$ ；

(3)、如图3，若 $C D = \frac{6 \sqrt{10}}{5}$ ，连接 $D M$ ，求 $△ M N D$ 的面积．

查看解析
5、如图1，在平面直角坐标系 $x O y$ 中，直线 $y = 2 x + 1$ 与反比例函数 $y = \frac{k}{x}$ 交于 $A (- 2, m)$ ， B两点，与x轴交于点C．

(1)、求反比例函数解析式；

(2)、P为反比例函数图象上任意一点（不与 $A 、 B$ 重合）
①过P作 $P Q ⊥ A B$ 交y轴于点Q，若 $P Q = 2 A C$ ，求P点坐标；
②如图2，直线 $P A$ 与x轴、y轴分别交于点 $M 、 N$ ，直线 $B P$ 分别与x轴y轴交于 $E 、 F$ ．试判断 $M E \cdot F N$ 是否为定值．若是，求出该值；若不是，请说明理由．

查看解析
6、2024年成都世园会吉祥物为“桐妹儿”，核心创意来自中国特有的孑遗植物珙桐（又称鸽子花）和三星堆“青铜神鸟”，寓意和平友好、包容互鉴，富有深刻的文化内涵和巴蜀特色．某商店购进“桐妹儿”的玩偶和钥匙扣，进货价分别为每个66元和59元，准备以每个88元和79元进行销售．

(1)、该店铺购进玩偶和钥匙扣共80个，若进货后能全部售出，则可获利1702元，问分别购进玩偶和钥匙扣多少个？

(2)、该店铺打算把钥匙扣调价销售，若按原价销售，平均每天可售8个，经调查发现，每降价1元，平均每天可多售2个，将销售价定为每个多少元时，能使钥匙扣平均每天销售利润为288元？

查看解析
7、在平面直角坐标系 $x O y$ 中，点 $A (0, 2)$ ，点 $B (2, 0)$ ，点 $C (0, - 2)$ ，点 $D (- 2, 0)$ ， $M$ 为四边形 $A B C D$ 边上一点．对于点 $P (6, 0)$ 给出如下定义：若 $∠ P M P_{1} = 90 °$ ， $P M = P_{1} M$ ，点 $P_{1}$ 在x轴下方，点 $P_{1}$ 关于原点的对称点为Q，我们称点Q为点P关于点M为直角顶点的“变换点”；则P关于点B为直角顶点的“变换点”坐标为；若直线 $y = k x + 3 k$ （ $k \neq 0$ ）上存在点P关于点M为直角顶点的“变换点”，则k的取值范围为．

查看解析
8、如图，在四边形 $A B C D$ 中， $A B ⊥ A D$ ， $A B = A C = 6$ ， $A D = 3$ ，点P是边 $A B$ 上一点， $A P = 4$ ，将线段 $A C$ 绕点A旋转，点C的对应点是E，连接 $A E ， P E ， D E$ ， $∠ C A E < ∠ C A D$ ，则 $2 D E + P E$ 的最小值为．

查看解析
9、如图1，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{12}{x} (x > 0)$ 的图象交于点 $A (a, 3)$ ，与 $y$ 轴交于点 $B (0, 1)$ ．

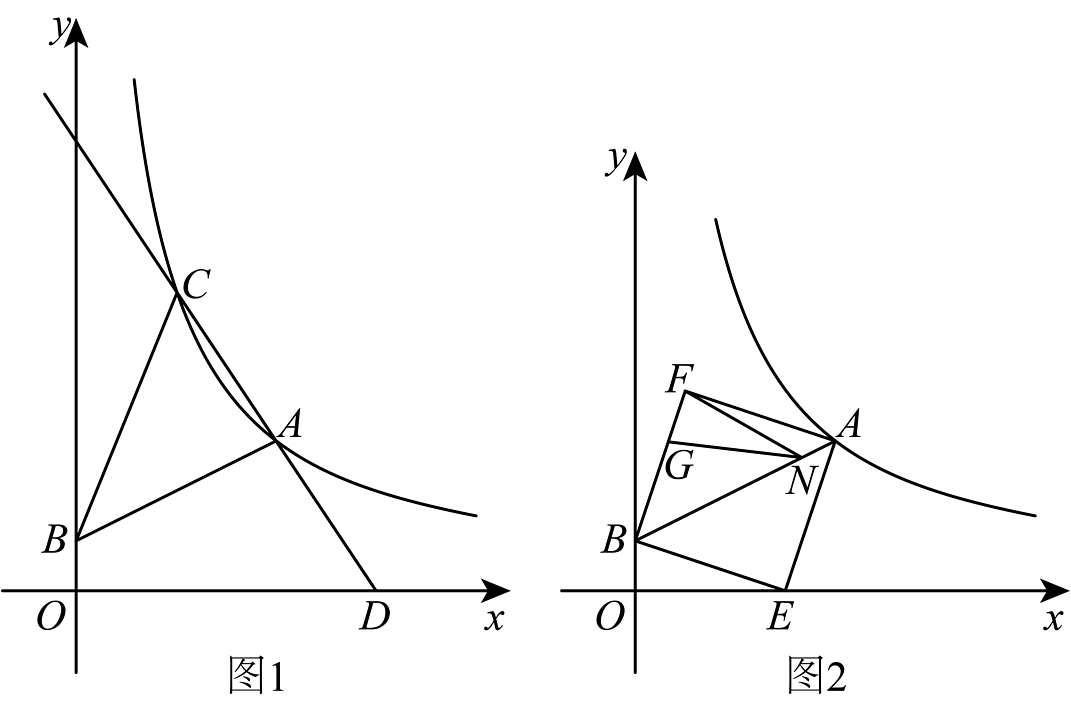(1)、求该一次函数的解析式；

(2)、在 $x$ 轴上有一点 $D (6, 0)$ ，直线 $A D$ 与反比例函数图象交于点 $C$ ，连接 $B C$ ．求 $△ A B C$ 的面积；

(3)、如图2，以线段 $A B$ 为对角线作正方形 $A E B F$ ，点 $G$ 是线段 $B F$ 上的一动点，点 $N$ 是线段 $A B$ 上的一动点，连接 $G N$ 、 $F N$ ，使 $∠ G N F = 2 ∠ A F N$ ，当点 $G$ 运动到 $B F$ 的三等分点时，求点 $N$ 的坐标．

查看解析
10、计算和解方程

(1)、计算： ${(- \frac{1}{2})}^{- 2} + |\sqrt{3} - 2| + \sqrt[3]{27} - {(3 - π)}^{0}$ ；

(2)、解方程： $x^{2} - 4 = 5 (x - 2)$ ．

查看解析
11、如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $B D$ 平分 $∠ A B C$ ，按如下步骤作图：第一步，分别以点B，D为圆心，以大于 $\frac{1}{2} B D$ 的长为半径作弧，两弧相交于点M和点N；第二步，作直线 $M N$ 分别交 $A B ， B D ， B C$ 于点E，O，F；第三步，连接 $D E 、 D F$ ．若 $D C = 4$ ， $D F = 5$ ，则 $A D$ 的长为．

查看解析
12、如图， $Rt △ A B C$ 中， $C D$ 是斜边 $A B$ 上的高， $A D = 6$ ， $B D = 3$ ，则 $D C =$ ．

查看解析
13、已知点 $A (x_{1}, y_{1})$ ， $B (x_{2}, y_{2})$ 是反比例函数 $y = \frac{3}{x}$ 图象上的两个点， $y_{1} < y_{2} < 0$ ，则 $x_{1}$ $x_{2}$ ．（填“ $>$ ”“ $<$ ”或“ $=$ ”）

查看解析
14、在平面直角坐标系 $x O y$ 中，矩形 $O A B C$ 位置如图放置，点A、C分别在x、y轴上，将 $O B$ 逆时针旋转到 $O B^{'}$ ，使得 $B^{'}$ 点落在x轴的负半轴上，连接 $B B^{'}$ ，交y轴于点D．若 $A B = 3, A O = 4$ ，则点D的纵坐标是（　　）

A、 $\frac{3}{2}$ B、 $\frac{4}{3}$ C、 $\frac{5}{3}$ D、 $\frac{7}{3}$

查看解析
15、如图， $△ A B C$ 与 $△ D E F$ 是位似图形，位似中心为 $O$ ， $O A : A D = 3 : 4$ ， $S_{△ A B C} = 9$ ，则 $△ D E F$ 的面积为（）

A、12 B、16 C、21 D、49

查看解析
16、如图，若D、E分别为 $△ A B C$ 中 $A B$ 、 $A C$ 边上的点，且 $∠ A E D = ∠ B$ ， $A D = 3$ ， $A C = 6$ ， $A B = 8$ ，则 $A E$ 的长度为（　　）

A、 $\frac{9}{4}$ B、 $\frac{5}{2}$ C、 $\frac{18}{5}$ D、4

查看解析
17、反比例函数的图象经过点 $A (- 3, 2)$ ，下列各点在此反比例函数图象上的是（　　）

A、 $(3, 2)$ B、 $(3, - 2)$ C、 $(6, 1)$ D、 $(- 6, - 1)$

查看解析
18、小明在学习历史时，想到可以用数轴上的点表示年份．由于历史上只有公元1年和公元前1年，没有公元0年，所以他制作了一条没有数0的“历史数轴”，其中公元前的年份表示为负数，如图所示．

(1)、记历史事件 $A$ 发生的年份为 $a$ ，历史事件 $B$ 发生的年份为 $b$ ，并记这条“历史数轴”上表示数 $a$ 和数 $b$ 的两个点之间的距离为 $T (A, B)$ ．
①据资料记载：
历史事件 $A$ ：公元前287年，阿基米德诞生；
历史事件 $B$ ：公元前212年，阿基米德逝世；
历史事件 $C$ ：公元前104年，我国古代第一部完整的历法《太初历》颁布实施；
历史事件 $D$ ：公元85年，《太初历》停止使用．
则 $T (A, B) =$ ___________； $T (C, D) =$ ___________（均用数字填空）；
②小明查阅了某初中数学教材中出现过的8位数学家的生卒年份，如下表所示：
数学家
徐光启
伽利略
牛顿
莱布尼兹
布丰
欧拉
高斯
华罗庚
生年
1562
1564
1642
1646
1707
1707
1777
1910
卒年
1633
1642
1727
1716
1788
1783
1855
1985
根据以上数据可知，在公元_________年，这8位数学家中同时在世的人数最多（填写一个年份即可，且不能填写表中已出现过的年份）；

(2)、小亮受“历史数轴”启发，也制作了一个有趣的“缺数码 $k$ 的数轴”（ $k =$ 2，3，…，9）：“数轴”上仍有原点和单位长度，自原点向右，距离原点1，2，3，4，…个单位长度的点表示的数仍为从小到大依次排列的正整数，但每个数中都不包含数码 $k$ ．例如，当 $k = 2$ 时，自原点向右，距离原点1，2，3，…，20，…个单位长度的点表示的数依次为1，3，4，5，6，7，8，9，10，11，13，14，15，16，17，18，19，30，31，33，…．记该“数轴”上表示正数 $a$ 和正数 $b$ 的两个点之间的距离为 $D (a, b)$ ．
①若 $D (24, 68) = 31$ ，则 $k$ 的值为__________；
②若 $m, n$ 为正整数， $m < n$ ，则 $D (10^{m}, 10^{n}) =$ __________（用含 $m, n$ 的式子表示）．

查看解析
19、已知关于 $x$ 的二次多项式 $(|k| - 1) x^{3} + (k + 1) x^{2} + 4 x - 3$ ．

(1)、直接写出 $k$ 的值；

(2)、若当 $x = m$ 时，该多项式的值是2，求 $[2024 k^{2} - m^{2} - 2 m]$ 的值．（其中 $[a]$ 表示不超过 $a$ 的最大整数，例如 $[3.1] = 3$ ．）

查看解析
20、在黑板上先依次写下两个正有理数 $a, b$ ，接下来对 $a, b$ 进行操作：
如果 $a > 0$ 且 $a < b$ ，则将 $2 a$ 和 $b - a$ 依次写在黑板上，作为新的 $a, b$ ，并将原 $a, b$ 擦掉；如果 $a > 0$ 且 $a \geq b$ ，则将 $a - b$ 和 $2 b$ 依次写在黑板上，作为新的 $a, b$ ，并将原 $a, b$ 擦掉；以上过程称为一次操作．只要黑板上新的 $a$ 满足 $a > 0$ ，就再进行下一次操作；如果新的 $a$ 满足 $a \leq 0$ ，则操作停止．

(1)、如果在黑板上先写下的数是 $a = 3, b = 9$ ，接下来进行几次操作后停止？说明理由：

(2)、如果在黑板上先写下的数是 $a = 1, b = 8$ ，则第 $2024$ 次操作后，黑板上的两个数依次是 $a =$ _________， $b =$ __________；

(3)、如果在黑板上先写下的是两个真分数 $a = \frac{1}{25}$ ， $b = \frac{p}{5}$ ，且进行有限次操作后，操作停止，则 $p$ 的所有可能值为__________．

查看解析

上一页 844 845 846 847 848 下一页跳转

数学家	徐光启	伽利略	牛顿	莱布尼兹	布丰	欧拉	高斯	华罗庚
生年	1562	1564	1642	1646	1707	1707	1777	1910
卒年	1633	1642	1727	1716	1788	1783	1855	1985