相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、抛物线先向右平移1个单位,再向上平移4个单位,平移后得到抛物线解析式为 .
-
2、抛物线的顶点坐标是 .
-
3、若二次函数的x和y的部分对应值如下,则下列说法错误的是( )
x
…
0
1
2
3
…
y
…
1.75
1.75
…
A、二次函数的图象与y轴的交点在y轴的负半轴上 B、对称轴为直线 C、当时,y随x的增大而增大 D、二次函数的图象与x轴交点的横坐标一个在和0之间,另一个在1和2之间 -
4、方程的根为( )A、 B、 , C、 D、 ,
-
5、在平面直角坐标系内,点关于原点对称的点的坐标是( )A、 B、 C、 D、
-
6、已知抛物线与x轴交于M、P两点,其中 .(1)、求抛物线解析式;(2)、如图1,点是抛物线上一点,N为抛物线第二象限一点,若 , 求N点坐标;
 (3)、如图2,点E为直线上一点,过E的直线、与抛物线均只有唯一公共点,连交直线于点D,若 , 求E点坐标.
(3)、如图2,点E为直线上一点,过E的直线、与抛物线均只有唯一公共点,连交直线于点D,若 , 求E点坐标.
-
7、在和中, , , , , 点F是线段的中点,连接 .(1)、若D在上,
①如图1,点E恰好落在上,请探究线段与的数量关系;
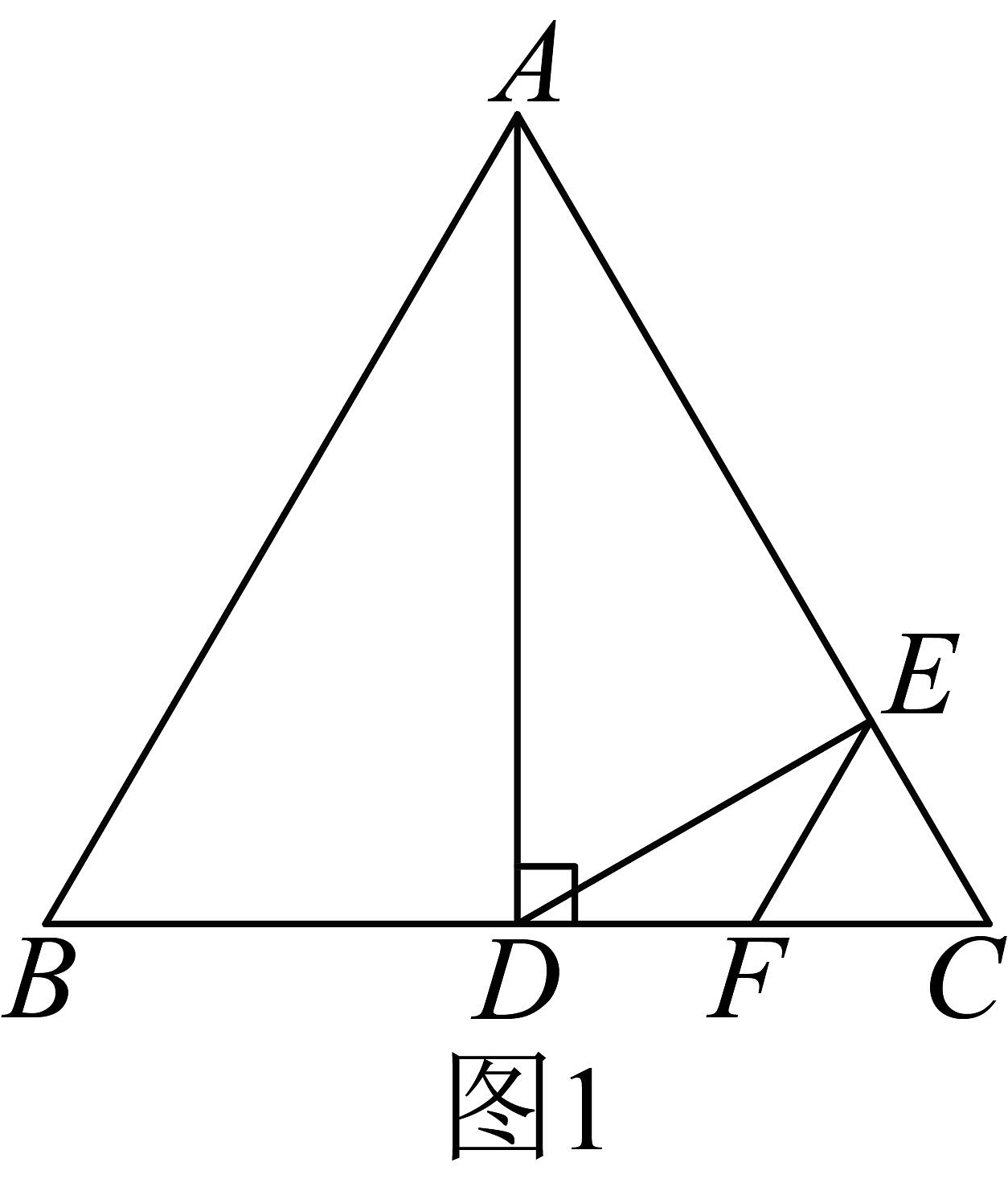
②如图2,试探究线段与的数量关系;
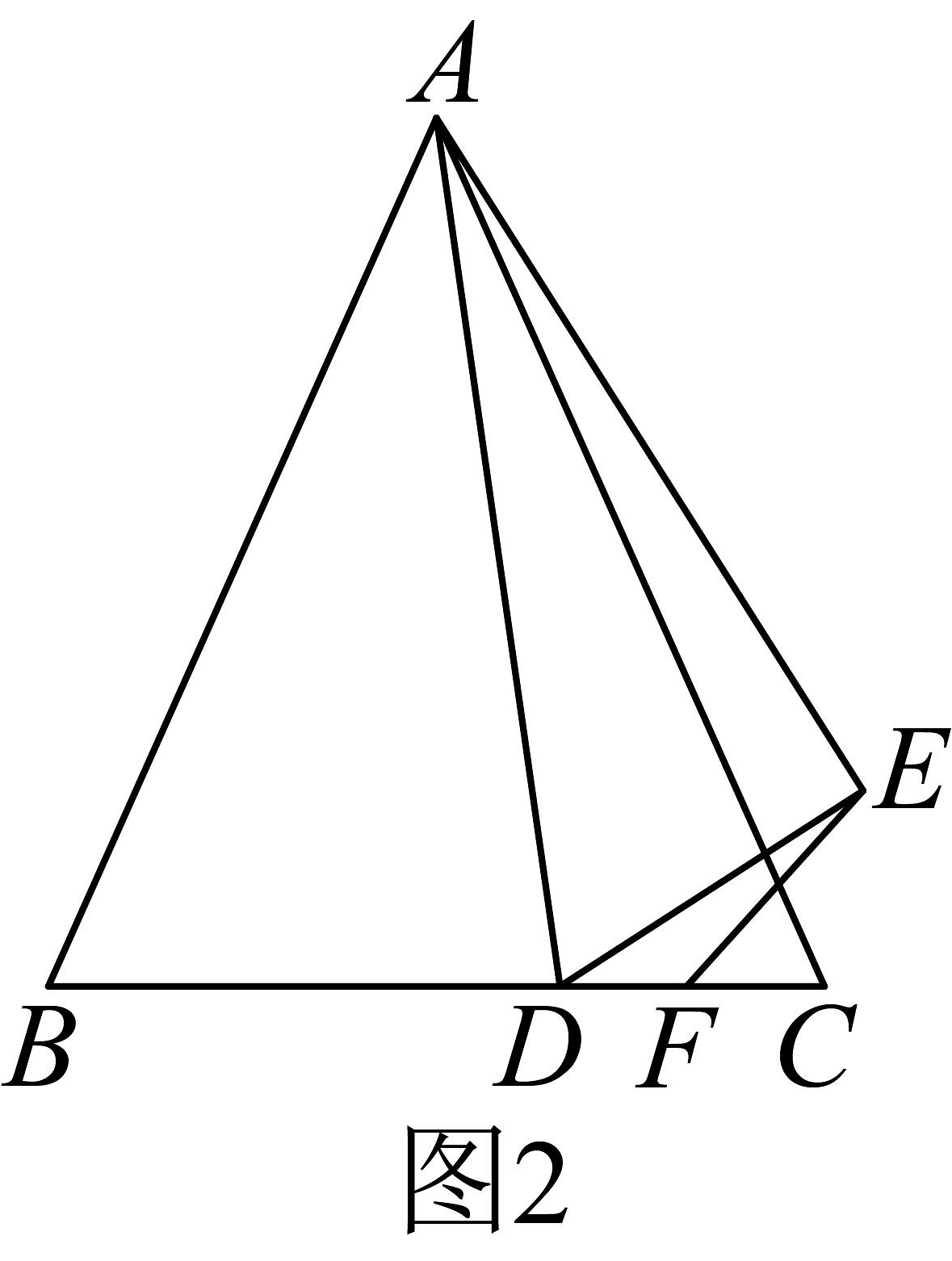 (2)、如图3, , 点D不在上, , , , 直接写出的面积是————·
(2)、如图3, , 点D不在上, , , , 直接写出的面积是————·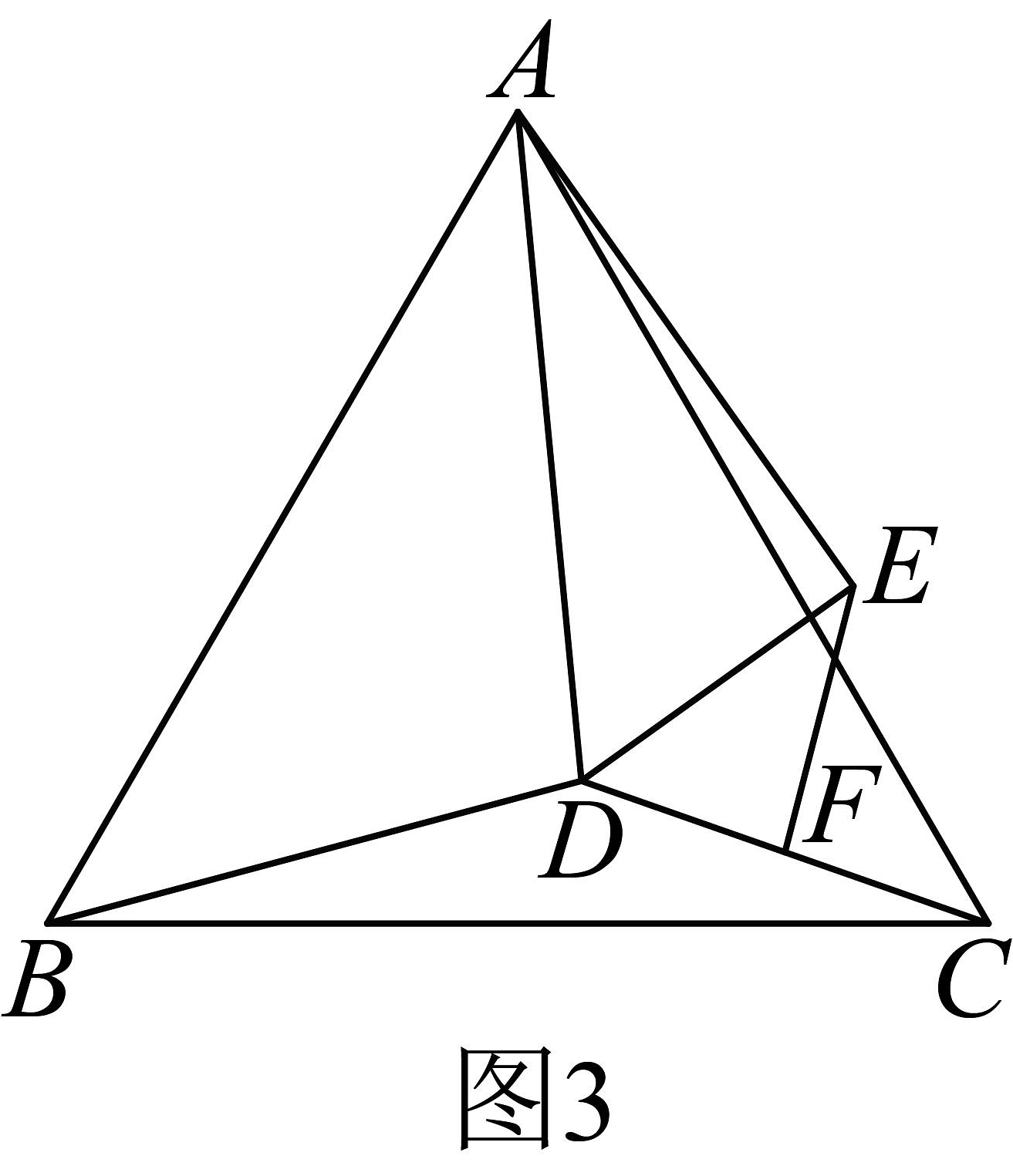
-
8、为适应武汉市体育新中考改革,学校购入一台羽毛球发球机,羽毛球球网飞行路线可以看作是抛物线的一部分,如图,建立平面直角坐标系,发球机放置在球场中央离球网水平距离的点O处,球从点O正上方的A处发出,其运行的高度与运行的水平距离满足关系式 . 身高为小明同学站在球网另一侧,且距离球网的水平距离处(如图所示),在头顶正上方至处称为有效击球高度﹒(球网高度不影响有效击球)
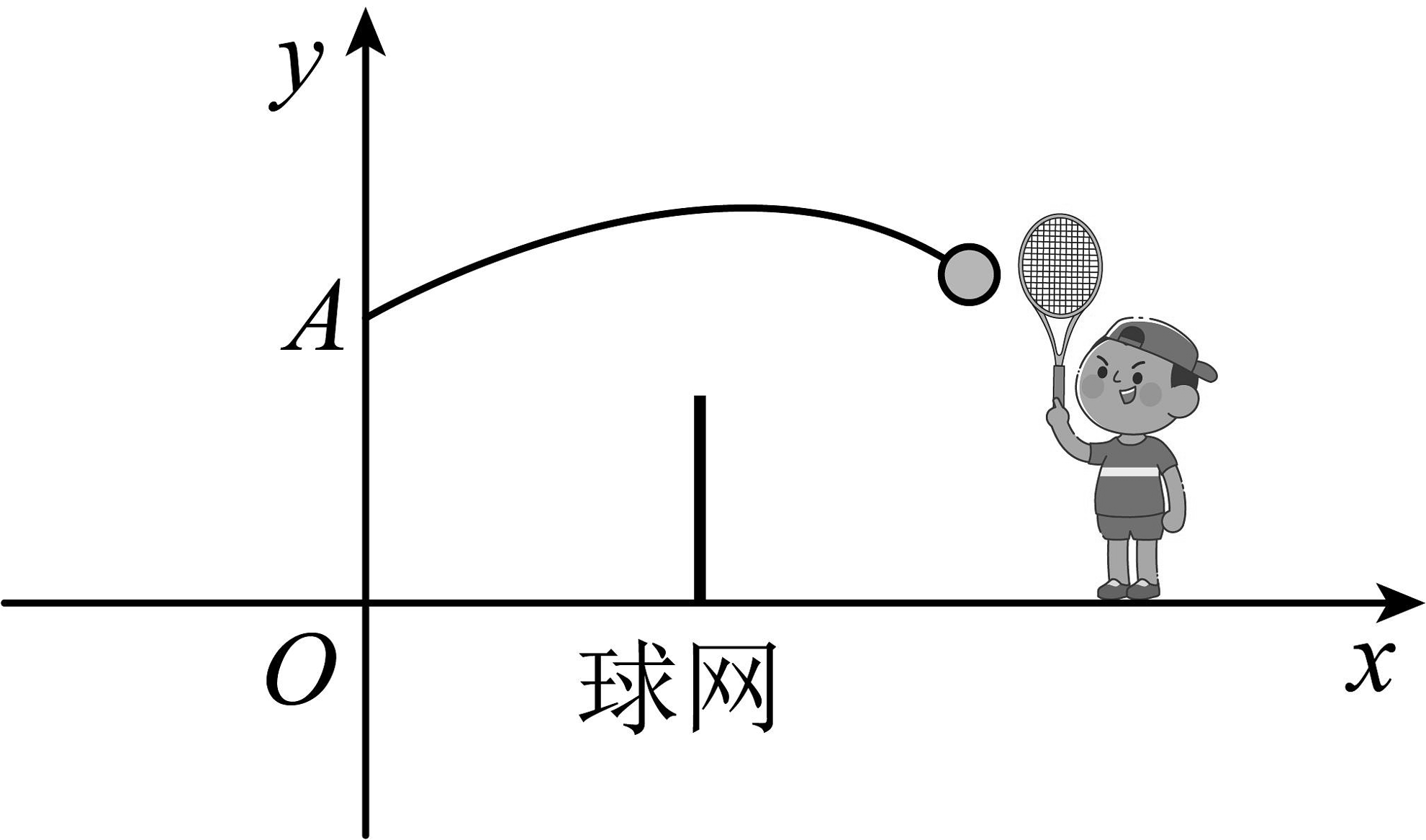 (1)、直接写出y与x的函数关系式(不必写自变量x的取值范围);(2)、试判断小明能否在原地有效击球,说明理由.(3)、为确保能够有效击球,当羽毛球在空中飞到最大高度时,小明决定向后退行.当羽毛球在空中飞到最大高度后,其飞行的水平速度保持为 , 此时小明必须在多长的时间内后退 , 使羽毛球恰好在头顶上方且完成有效击球?
(1)、直接写出y与x的函数关系式(不必写自变量x的取值范围);(2)、试判断小明能否在原地有效击球,说明理由.(3)、为确保能够有效击球,当羽毛球在空中飞到最大高度时,小明决定向后退行.当羽毛球在空中飞到最大高度后,其飞行的水平速度保持为 , 此时小明必须在多长的时间内后退 , 使羽毛球恰好在头顶上方且完成有效击球? -
9、如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.三个顶点都是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过四条.
 (1)、在图(1)中,先画格点D,使得于E;(2)、在(1)的基础上,在射线上画一点F,使得;(3)、在图(2)中,先画点P,使点A绕点P逆时针旋转得点C,连接交于G;(4)、在(3)的基础上,将线段绕点G旋转 , 画出对应线段(点B与点M对应,点C与点N对应).
(1)、在图(1)中,先画格点D,使得于E;(2)、在(1)的基础上,在射线上画一点F,使得;(3)、在图(2)中,先画点P,使点A绕点P逆时针旋转得点C,连接交于G;(4)、在(3)的基础上,将线段绕点G旋转 , 画出对应线段(点B与点M对应,点C与点N对应). -
10、抛物线的图像与x轴交于A,B两点,A在B左侧,与y轴交于点C.
 (1)、点C坐标为 , 顶点坐标为 ;(2)、不等式的解集是 ;(3)、当x满足时,y的取值范围是 .(4)、当y满足时,x的取值范围是 .
(1)、点C坐标为 , 顶点坐标为 ;(2)、不等式的解集是 ;(3)、当x满足时,y的取值范围是 .(4)、当y满足时,x的取值范围是 . -
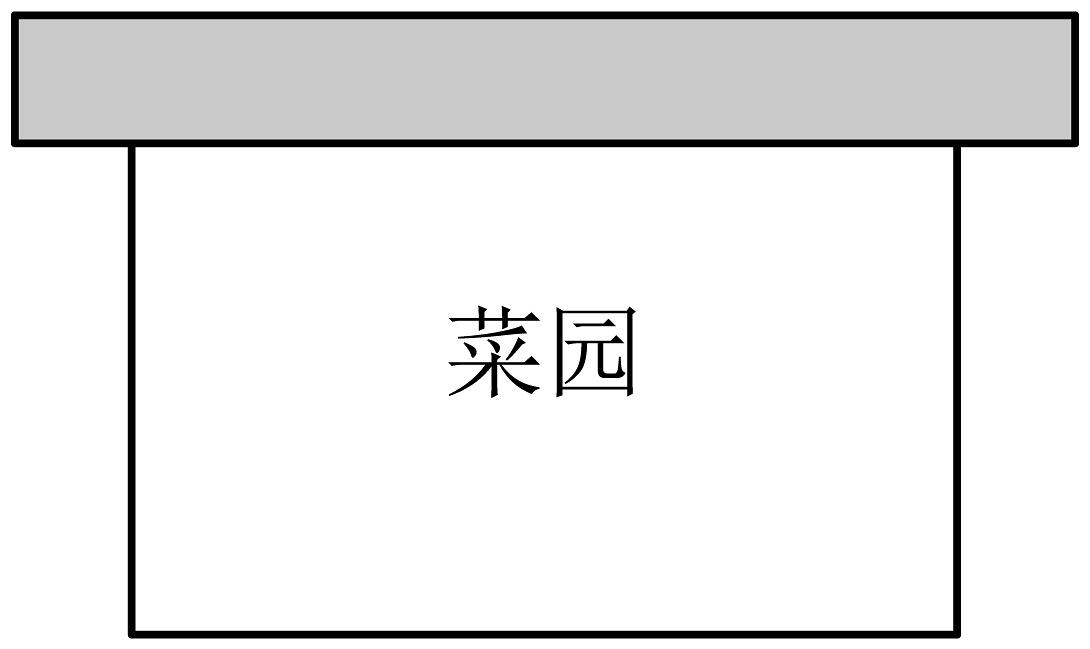
11、如图,用一段长为32米的篱笆围成一个矩形菜园,其中一面靠墙,墙长为14米,若矩形菜园的面积为96米 , 求矩形菜园垂直于墙的边长.
-
12、已知抛物线的y与x的部分对应值如表:
下列结论:
①对称轴为直线;
②方程有两个不相等的实数根;
③若点 , 均在二次函数图象上,则;
④满足的x的取值范围是或 .
其中正确结论的序号为 .
-
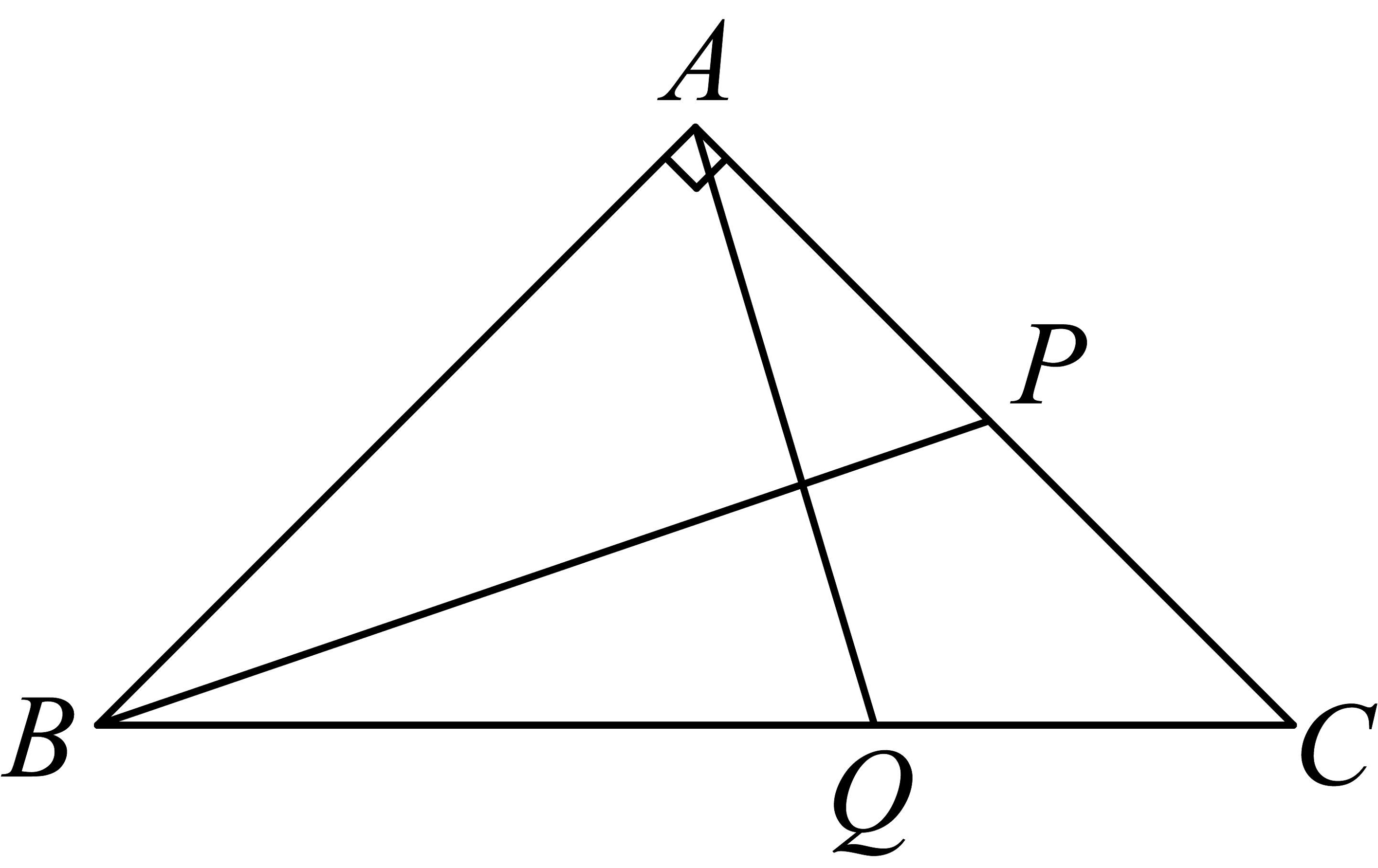
13、如图,在中, , , 点P,Q分别为边 , 上的动点,且 , . 当的值最小时,的长为 .
-
14、将抛物线向下平移k个单位后与坐标轴仅有两个交点,则 .
-
15、为增强学生身体素质,提高学生足球运动竞技水平.某区开展“健身杯”足球比赛,赛制为单循环形式(每两个队之间赛一场),现计划一共安排28场比赛,则应邀请 个足球队参赛.
-
16、若一元二次方程的两个实数根为m,n,则的值为 .
-
17、抛物线在直线下方的图像上恰好有五个横坐标为整数的点,则k的值不可能是( )A、 B、 C、13 D、
-
18、第十四届国际数学教育大会(ICME-14)在中国上海举行,会徽(如图)的主题图案有着丰富的数学元素,展现了我国古代数学的文化魅力,其右下方的“卦”是用我国古代的计数符号写出的八进制数3745.八进制是以8作为进位基数的数字系统,有0~7共8个基本数字.八进制数3745换算成十进制是 , 表示ICME-14的举办年份.小婷设计了一个m进制数165,换算成十进制数是96,则m的值为( )
 A、12 B、10 C、8 D、7
A、12 B、10 C、8 D、7 -
19、已知点在二次函数的图象上,二次函数图象与y轴的交点在负半轴,则的大小关系为( )A、 B、 C、 D、
-
20、抛物线图象向左平移3个单位,再向上平移2个单位,所得图象的解析式为 , 则的值为( )A、 B、 C、 D、