相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、某超市一月份的营业额为万元,已知第一季度的总营业额共万元.如果平均每月增长率为 , 则由题意列方程应为( )A、 B、 C、 D、
-
2、用配方法解方程时,配方后正确的是( )A、 B、 C、 D、
-
3、将一元二次方程化成一般形式后,常数项为 , 二次项系数和一次项系数分别是( )A、2, B、2,5 C、 , D、 , 5
-
4、如图,要把河中的水引到村庄 , 小凡先作 , 垂足为点 , 然后沿开挖水渠,就能使所开挖的水渠最短,其依据是 .
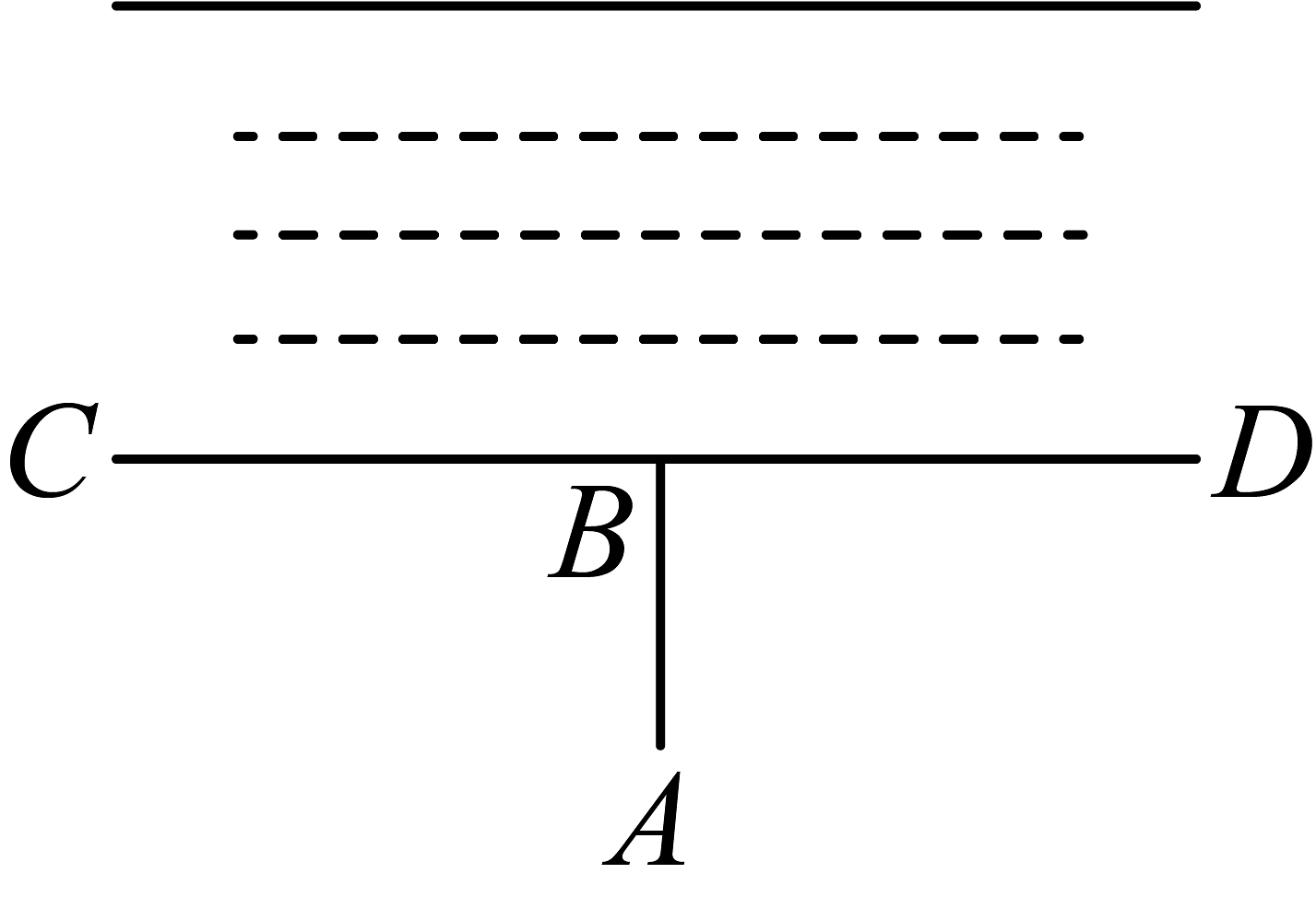
-
5、【问题呈现】阅读材料1:若四边形内存在一点到四个顶点的距离相等,我们把这个点叫做四边形的“开心点”.
阅读材料2:关于的一元二次方程 , 如果 , , 满足且 , 那么我们把这样的方程称为“2倍—勾系方程”.
【问题解决】(1)在①平行四边形,②矩形,③菱形,④正方形这四种四边形中,一定存在“开心点”的四边形的是( )
A.①② B.③④ C.②③ D.②④
(2)求证:关于的“2倍—勾系方程”必有实数根;
【问题应用】(3)如图,已知四边形存在“开心点” , 且到四个顶点的距离为 , , , , , 且关于的方程是“2倍—勾系方程”.

①求证:;
②直接写出的长(用 , 的式子表示).
-
6、我们约定:在平面直角坐标系中,若点满足 , 我们就说点是该平面直角坐标系内的“大九中”点,若函数图象上存在一个或以上的“大九中”点的函数我们称之为“幸福函数”.根据约定请解决以下问题:(1)、若反比例函数是“幸福函数”,请问是否是该函数图象上的“大九中”点?(填“是、否”即可)(2)、若函数是“幸福函数”且函数图象上有两个“大九中”点,求的取值范围;(3)、若反比例函数的图象上存在两个“大九中”点为 , 且 , 求的值.
-
7、请阅读以下材料,并完成相应的问题:角平分线分线段成比例定理:如图1,在△ABC中,AD平分∠BAC,则 , 下面是这个定理的部分证明过程:

证明:如图2,过C作CEDA,交BA的延长线于E.…
任务:
(1)、请按照上面的证明思路,写出该证明的剩余部分;(2)、如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,求BD的长.(请按照本题题干的定理进行解决) -
8、暑假期间,为了加强青少年积极参加体育锻炼,某体育用品店开展乒乓球拍促销活动.(1)、据市场调研发现,某体育用品店近几个月的乒乓球拍销售量逐月提升,已知6月共销售乒乓球拍副,每月的月销售增长率相同,8月共销售副,求该乒乓球拍6月份到8月份销售量的月平均增长率;(2)、已知某体育用品店乒乓球拍平均每天可销售副,每副盈利元,每下降1元,则每天可多售4副,在每副降价幅度不超过元的情况下,如果每天要盈利元,则每副乒乓球拍应降价多少元?
-
9、近日,火爆全网的泰山“机器狗”搬运货物事件引发人们的热议,这不仅是一次科技现象,更是智能时代来临的信号.我们应当认识到,随着科技的发展,“机器狗”等智能设备即将融入我们的日常生活.若“机器狗”最快移动速度是载重后总质量的反比例函数,即 . 已知一款“机器狗”载重后总质量时,它的最快移动速度 .(1)、求与的解析式;(2)、若机器狗载重后总质量为时,它的最快移动速度为多少?
-
10、计算:(1)、;(2)、 .
-
11、如图,中, , , , 为的中点,若动点以的速度从点出发,沿向点运动,设点的运动时间为秒,连接 , 当以 , , 为顶点的三角形与相似时,的值为 .

-
12、用因式分解法解一元二次方程,方程可化为 , 则 .
-
13、如图,以点为位似中心,作四边形的位似图形 , 已知 , , 若四边形的面积为 , 则四边形的面积为 .

-
14、若点和点在反比例函数图象上,则与的大小关系是:(填“”、“”或“”).
-
15、若 , 则的值是 .
-
16、一次函数和反比例函数的图象如图所示,若 , 则的取值范围是( )
 A、或 B、或 C、或 D、或
A、或 B、或 C、或 D、或 -
17、如图,在一块矩形的劳动实践基地上有三条同宽的道路,横向有一条,纵向有两条,除道路外,剩下的是种植面积.已知该矩形基地的长为米,宽为米,种植面积为平方米,设修建的路宽为米,根据题意可列方程为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
18、观察下面的表格:
判断方程的其中一个解的范围是( )
A、 B、 C、 D、 -
19、关于的一元二次方程的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、有一个实数根 D、没有实数根
-
20、大自然鬼斧神工,一片小小的树叶,也蕴含着“黄金分割”的美.黄金分割比是指将整体一分为二,较长线段与整体线段长度的比值等于较短线段与较长线段长度的比值,其比值为 如图,P为线段AB的黄金分割点(),.如果的长度为 , 那么的长度是( )
 A、 B、 C、 D、
A、 B、 C、 D、