相关试卷

1、在实数2， $- 3$ ， 0， $- \frac{1}{4}$ 这四个数中，最小的数是（）

A、2 B、 $- 3$ C、0 D、 $- \frac{1}{4}$

查看解析
2、如图，平面直角坐标系中， $A (- 2 ， 1)$ ， $B (- 3 ， 4)$ ， $C (- 1 ， 3)$ ，过点 $(1 ， 0)$ 作x轴的垂线 $l$ ．


(1)、画出 $△ A B C$ 关于直线 $l$ 的轴对称图形 $△ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标．

(2)、 $△ A B C$ 的面积为

(3)、在 $△ A B C$ 内有一点 $P (m, n)$ ，则点P关于直线 $l$ 的对称点R的坐标为（         ，        ）（结果用含m，n的式子表示）．

查看解析
3、如图，BD是△ABC的角平分线，AE丄BD交BD的'延长线于点E， ∠ABC = 72°，∠C：∠ADB =2：3，求∠BAC 和∠DAE 的度数.

查看解析
4、如图， $△ A B C$ 是等边三角形，点E在AC的延长线上，点D在线段AB上，连接ED交线段BC于点F，过点F作 $F N ⊥ A C$ 于点N， $D B = \frac{7}{5} C N$ ， $E F = F D$ ，若 $F B = 17$ ，则AN的长为．

查看解析
5、一个正多边形的一个外角等于它的一个内角的 $\frac{1}{3}$ ，这个正多边形是边形．

查看解析
6、如图，在等腰三角形 $A B C$ 中， $A B = A C = 13$ ， $B C = 10$ ， $D$ 是边 $B C$ 上的中点， $A D = 12$ ， $M$ ， $N$ 分别是 $A D$ 和 $A B$ 上的动点，则 $B M + M N$ 的最小值是（）

A、10 B、 $\frac{60}{13}$ C、13 D、 $\frac{120}{13}$

查看解析
7、如图，已知 $△ E F G ≌ △ N M H$ ，则下列说法错误的是（）

A、 $E G = H G$ B、 $E G ∥ H M$ C、 $∠ F E G = ∠ M N H$ D、 $E F = N M$

查看解析
8、同学们试着用数学的眼光观察世界，下列图形中，没有运用到三角形的稳定性的是（）

A、 B、 C、 D、

查看解析
9、我国古代数学名著《算法统宗》有一道“荡秋千”的问题：“平地秋千未起，踏板一尺离地．送行8尺与人齐，5尺人高曾记，仕女家人争蹴．良工高士素好奇，算出索长有几？”此问题可理解为：“如图，有一架秋千，当它静止时，踏板离地距离 $D E$ 的长为1尺，将它向前水平推送8尺时，即 $B C = 8$ 尺．秋千踏板离地的距离 $B F$ 和身高5尺的人一样高，秋千的绳索始终拉得很直，试问绳索有多长？”请运用所学知识求出秋千的长是尺．

查看解析
10、抛物线 $y = \frac{1}{4} x^{2} - 3$ 与直线y=x交于A ， B两点(A在B的左边).y=x

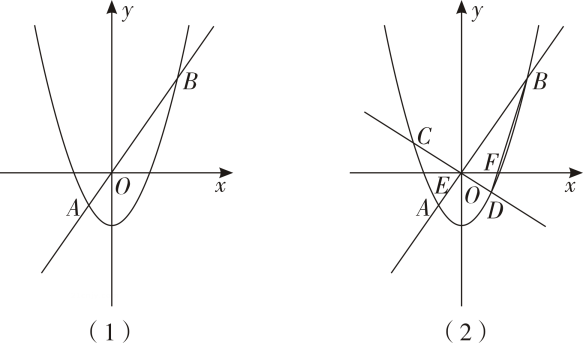(1)、求A ， B两点的坐标.

(2)、如图1，若P是直线AB下方抛物线上的点.过点P作x轴的平行线交抛物线于点M ，过点 P作y轴的平行线交线段AB于点N ，满足PM=PN 求点P的横坐标.

(3)、如图2，经过原点O的直线CD交抛物线于C ， D两点(点C在第二象限)，连接AC ， BD分别交x轴于E ， F两点.若 $S_{△ D O F} = \frac{4}{3} S_{△ C O F}$ 求直线CD的解析式.

查看解析
11、如图，四边形ABCD是正方形，点E在边CD上，点F在边BC的延长线上，DE=CF 射线AE交对角线BD于点G ，交线段DF于点H.

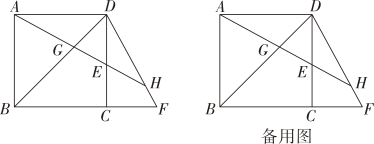(1)、求证： DH=GH (温馨提示：若思考有困难，可尝试证明. $△ A D E ≅ △ D C F$

(2)、求证： $A G \cdot E H = E G \cdot G H$

(3)、若 $\frac{G E}{E H}$ =n直接写出 $\frac{D H}{D F}$ 的值(用含n的式子表示).

查看解析
12、某校数学小组开展以“羽毛球飞行路线”为主题的综合实践活动.
【研究背景】羽毛球飞行路线所在的平面与球网垂直.
【收集数据】某次羽毛球飞行的高度y(单位：m)与距发球点的水平距离x(单位：m)的对应值如下表(不考虑空气阻力).
水平距离x/m
0
2
3
5
6
…
竖直高度y/m
1.1
2.3
2.6
2.6
2.3
…
【探索发现】数学小组借助计算机画图软件，建立平面直角坐标系、描点、连线(如图)，发现羽毛球飞行路线是抛物线 y=ax²+kx+1.1的一部分.
【建立模型】求y与x的函数解析式(不要求写自变量取值范围).
【应用模型】

(1)、羽毛球在此次飞行过程中，飞行的高度能否达到2.8m?请说明理由.

(2)、保持羽毛球飞行路线对应的抛物线的形状不变，改变发球方式，使其解析式变为y=ax²+kx+1.1发球点与球网的水平距离是5m.若羽毛球飞过球网正上方时，飞行的高度超过2.1m ，且球的落地点与球网的水平距离小于6m.求k的取值范围.

查看解析
13、如图是由小正方形组成的3个4闷格，每个小正方形的顶点叫作格点，矩形ABCD的四个顶点都是格点.仅用无刻度直尺在给定网格中完成如下两个问题，每个问题的画线不得超过五条.

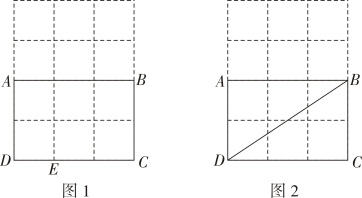(1)、如图1，E是格点，先将点E绕点A逆时针旋转( $90 °$ ，画对应点 F ，再画直线FG交AB于点G ，使直线FG-平分矩形ABCD的面积.

(2)、如图2，先画点C关于直线BD的对称点M ，再画射线MN交BD于点N ，使MN∥AD

查看解析
14、如图，点A ， B ， C ， D在⊙O上，BD是直径， $∠ B A C = 45 °$ ，过点C作CE∥BD交AB的延长线于点E.

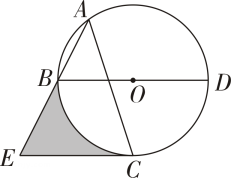(1)、求证：CE是⊙O的切线.

(2)、若 $B D = 4 ∠ A B D = 2$ ，求图中阴影部分的面积.

查看解析
15、某校开展“中国诗词”竞赛，学生成绩为正整数，满分为5分.为了解本次竞赛的情况，从该校随机抽取m名学生的成绩作为样本，将收集的数据整理并绘制成如下两幅不完整的统计图.根据以上信息，解答下列问题：

(1)、m的值是，扇形统计图中“5分”对应的扇形的圆心角大小是.

(2)、该校共有1000名学生参加竞赛，估计成绩超过3分的学生人数.

(3)、从样本的众数、中位数中选择一个统计量，写出它的值并说明它的实际意义.

查看解析
16、如图，四边形ABCD的对角线交于点O ， AD∥BC.若 ▲ ，则AD=CB
从①OA=OC ， ②∠ABC=∠CDA ， ③AB=CD这三个选项中选择一个作为条件，使结论成立，并说明理由.

查看解析
17、解不等式组 ${\begin{cases} 3 x - 5 \leq 1 ① \\ 2 x + 1 ＞ x ② \end{cases}$

查看解析
18、已知二次函数y= ax²+(a-2)x-2(a为常数，且a≠0).下列五个结论：
①该函数图象经过点(-1，0)；
②若a=-1，则当x＞-1时，y随x的增大而减小；
③该函数图象与x轴有两个不同的公共点；
④若a＞2，则关于x的方程.ax²+(a-2)x-2=0有一个根大于0且小于1；
⑤若a＞2，则关于x的方程 | ax²+(a-2)x-2|=2的正数根只有一个.
其中正确的是(填写序号).

查看解析
19、如图，在△ABC中，AB=AC=10，BC=2 $\sqrt{10}$ ，点D在边AC上，CD=3.若点E在边AB上，满足CE=BD ，则AE的长是.

查看解析
20、某科技小组用无人机测量一池塘水面两端A ， B的距离，具体过程如下：如图，将无人机垂直上升至距水面120m的P处，测得A处的俯角为 45°B处的俯角为 22°，则A ， B之间的距离是m.(tan22°取0.4)

查看解析

上一页 838 839 840 841 842 下一页跳转

水平距离x/m	0	2	3	5	6	…
竖直高度y/m	1.1	2.3	2.6	2.6	2.3	…