相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、某商店以20元/千克的单价购进一批商品,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间存在一次函数关系,对应数值如下表所示.
销售单价x(元/千克)
25
35
销售量y(千克)
50
30
(1)、求y与x之间的函数关系式;(2)、现要求尽快售完该商品,并使销售利润达到400元,求销售单价应定为每千克多少元?(3)、售完该商品后,销售利润能达到500元吗?若能,求出此时的销售单价;若不能,请说明理由. -
2、拉杆箱是外出旅行常用工具.某种拉杆箱示意图如图所示(滚轮忽略不计),箱体截面是矩形 , 的长度为 , 两节可调节的拉杆长度均等于 , 且与在同一条直线上.
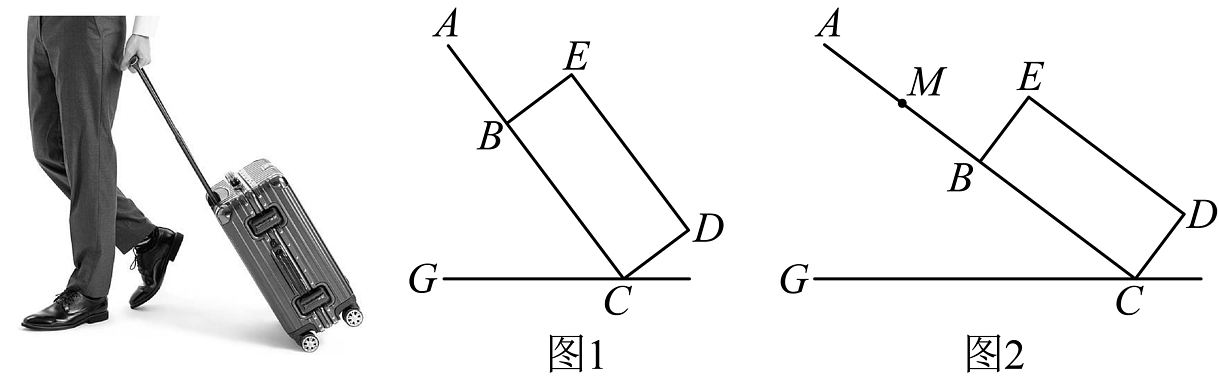 (1)、如图1,当拉杆伸出一节时,与地面夹角 , 求出此时拉杆把手A点距离地面的高度;(2)、如图2,当拉杆伸出两节()时,此时拉杆把手A点距离地面高度与图1相同.求出此时与地面夹角的度数.(参考数据: , )
(1)、如图1,当拉杆伸出一节时,与地面夹角 , 求出此时拉杆把手A点距离地面的高度;(2)、如图2,当拉杆伸出两节()时,此时拉杆把手A点距离地面高度与图1相同.求出此时与地面夹角的度数.(参考数据: , ) -
3、在物理实验室小红设计了杠杆平衡实验:如图,取一根长且质地均匀的木杆,用细绳绑在木杆的中点O处并将其吊起来,在左侧距离中点O处挂一个重的物体,为了保持木杆水平(动力×动力臂=阻力×阻力臂),在中点O右侧用一个弹簧测力计竖直向下拉,改变弹簧测力计与中点O距离 , 看弹簧测力计的示数的变化情况.在做此实验后,得到的数据如表所示.
第1组
第2组
第3组
第4组
L/cm
a
30
32
37.5
F/N
4.8
4
b
3.2
 (1)、在已学过的函数中选择合适的模型,求与的函数表达式;(2)、补充表中数据:______,______;(3)、在实验中发现,在弹簧测力计承受范围内,为了保持木杆水平,弹簧测力计越靠近中心点O,弹簧测力计示数就______
(1)、在已学过的函数中选择合适的模型,求与的函数表达式;(2)、补充表中数据:______,______;(3)、在实验中发现,在弹簧测力计承受范围内,为了保持木杆水平,弹簧测力计越靠近中心点O,弹簧测力计示数就______A.变大 B.变小 C.不变
(4)、若弹簧测力计的最大量程是 , 求L的取值范围. -
4、某中学为了解初三同学身体素质,随机抽取该年级某班学生进行体育模拟测试(满分30分),根据测试成绩(单位:分)绘制成两幅不完整的统计图(如图1和图2),已知图2中测试成绩29分所对应的圆心角为 , 回答下列问题:
 (1)、条形统计图1有一部分污损了,求测试成绩28分的人数;(2)、求出该班的平均成绩;直接写出所调查学生测试成绩中位数和众数;(3)、现有n名同学因病错过考试,补测后与之前成绩汇总,发现中位数变大了,则n的最小值 .
(1)、条形统计图1有一部分污损了,求测试成绩28分的人数;(2)、求出该班的平均成绩;直接写出所调查学生测试成绩中位数和众数;(3)、现有n名同学因病错过考试,补测后与之前成绩汇总,发现中位数变大了,则n的最小值 . -
5、已知一元二次方程:(1)、方程有两个不相等的实数根,求k的取值范围;(2)、若方程一个根为2,求方程的另一根.
-
6、如图,将图所示的正方形纸片剪成四块,恰好拼成图所示的矩形,若 , 则 .
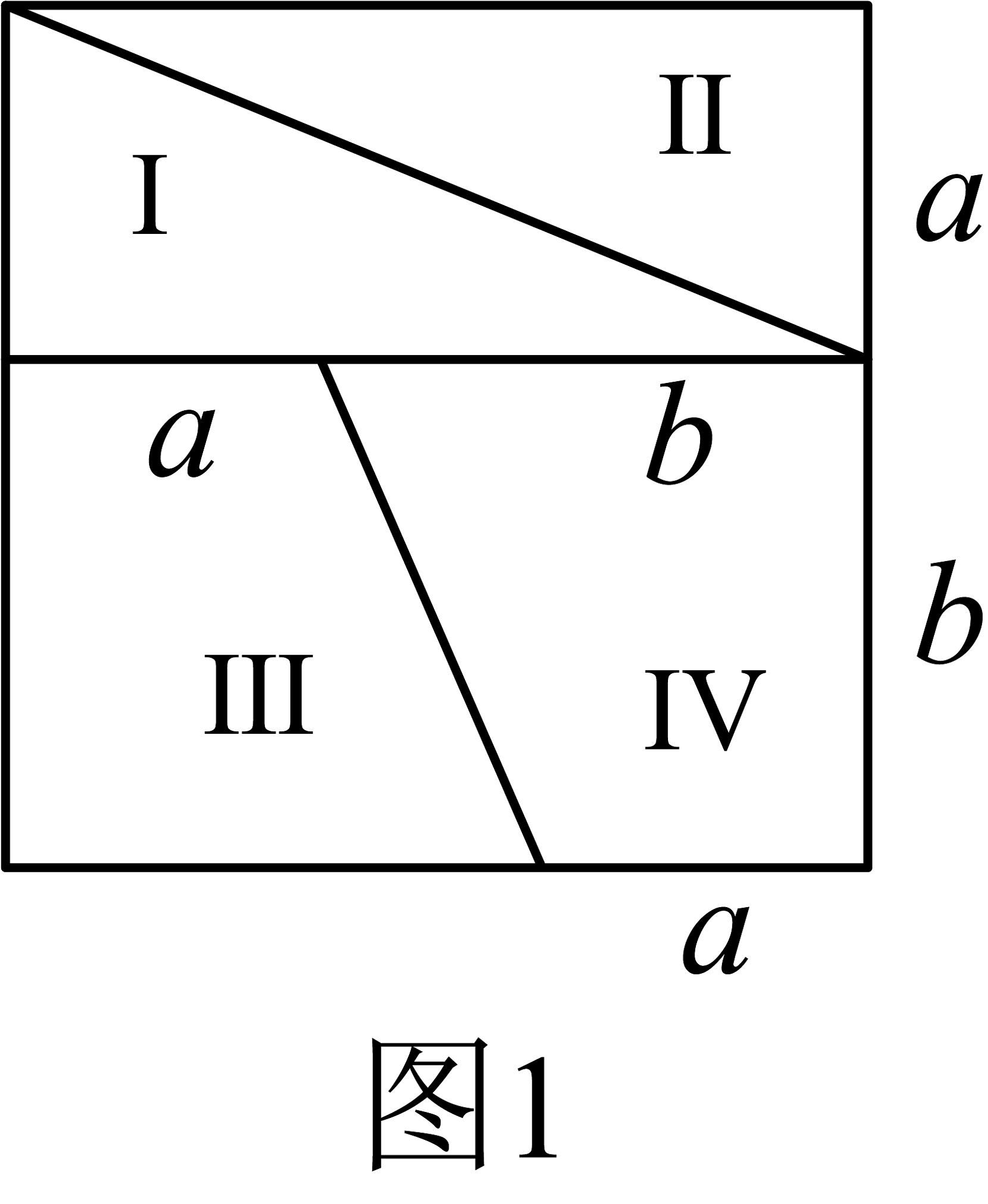

-
7、某超市销售A、B、C三种不同型号的手电筒,它们的单价分别为16元,20元,30元,某天该超市的手电筒销售数量情况如图所示,那么这天该超市销售的手电筒每个平均价格是元.

-
8、反比例函数的图象经过两点,当时, , 请写出一个符合条件的的值 . (只需写出一个即可)
-
9、如图,直线m,n,l分别经过正方形的顶点A、B、C,且 , 直线n与交于点E,若m与n之间的距离是3,n与l之间的距离是4,则的值为( )
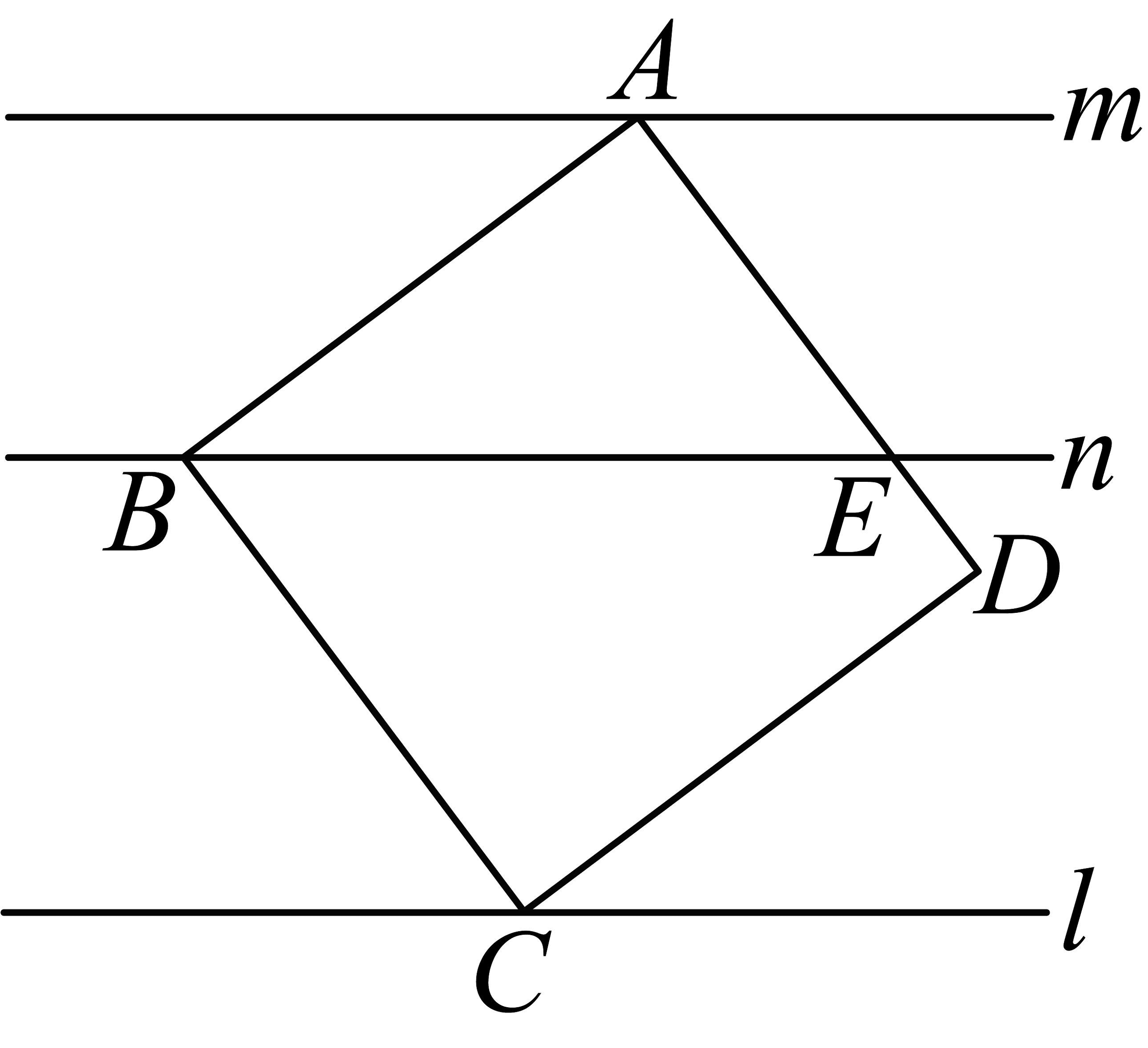 A、 B、 C、 D、
A、 B、 C、 D、 -
10、全民健身成为一种新时尚.淇淇在长为的路段上进行骑车训练,若行驶全程所用的时间为 , 行驶的平均速度为 . 下列说法错误的是( )A、若 , 则 B、若 , 则 C、若t减小,则v也减小 D、若t减小一半,则v增大一倍
-
11、淇淇在计算正数a的平方时,误算成a与2的积,求得的答案比正确答案小3,则( )A、 B、3 C、 D、1或3
-
12、下表是某社团14名成员的年龄分布统计表,数据不小心被墨水覆盖一部分,仍能够分析得出这14名成员年龄的统计量的是( )
 A、平均数 B、方差 C、众数 D、中位数
A、平均数 B、方差 C、众数 D、中位数 -
13、关于x的一元二次方程的两个根为和 , 且 , , 则这个一元二次方程可以是( )A、 B、 C、 D、
-
14、甲、乙、丙三名射击运动员进行射击测试,每人10次射击绩的平均数(单位:环)及方差(单位:环2)如表所示,根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
甲
乙
丙
9
8
9
1.2
0.4
1.8
A、甲 B、乙 C、丙 D、无法确定 -
15、某班数学考试后,同学们很关心自己的成绩水平,为了让学生估计自己的成绩水平,老师应该公布成绩的哪些统计量( )A、中位数和平均数 B、众数和中位数 C、方差 D、众数和平均数
-
16、如图是嘉嘉的作业,其中括号内应填的内容是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、如图,从点D观测点E的俯角是 , 则在点E观测点D的仰角是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
18、如图,从放大镜里看到的三角尺与原来的三角尺之间的图形变换属于( )
 A、平移 B、旋转 C、相似 D、轴对称
A、平移 B、旋转 C、相似 D、轴对称 -
19、下列式子是最简二次根式的是( )A、 B、 C、 D、
-
20、在十一作业中同学们参与了“自制角分仪”的活动,下图是一个同学的作品,他将四根木条顺次钉在一起,其中 , , 两根木条的连接处是可以转动的.(1)、如图是一种用四根木条钉成的平分角的仪器,其中 , , 相邻两根木条的连接处是可以转动的.在下面的几种用法中,能作出的平分线的有_______________.(填写序号)



①是的平分线
②是的平分线
③是的平分线
(2)、对于这个工具的其它用途,小泽发现可以用它作线段的垂直平分线.请结合右图补全求证,并给出证明.
如图,已知: , .

求证:______________垂直平分_____________.
证明:
(3)、小瑞同学们在探究的过程中又计出了三等分角的仪器一一勾尺.
勾尺的直角顶点为 , (“宽臂”的宽度) , 勾尺的另一边为 , 且满足 , , 三点共线(所以).
小瑞利用手中的勾尺,通过下列步骤将三等分:
第一步:如图1,画直线使 , 且这两条平行线的距离等于;
第二步:如图2,移动勾尺到合适位置,使顶点落在上,使边经过点 , 同时让点落在的边上;
第三步:如图3,标记此时点和点所在位置,作射线和射线 .
然后小瑞利用图3,证明射线和射线是的三等分线,请补全证明过程:
证明:垂直平分线段 ,
_____________________.
,
.
(请继续完成后面的证明过程)