相关试卷

1、我国很多经典古籍中记载了“河图洛书”，它是中国重要的文化遗产．其中洛书（如图1）可以用三阶幻方表示（如图2），就是将已知9个数填入 $3 \times 3$ 的方格中，使每一行、每一竖列以及两条斜对角线上的数字之和都相等．在图3的幻方中也有与图2相同的数字之和的规律，给定 $a$ 、 $b$ 、 $c$ 、 $d$ 中一个字母的值不能补全图3的是（）

A、 $a$ B、 $b$ C、 $c$ D、 $d$

查看解析
2、求下列各式的值．

(1)、先化简，再求值， $3 (x^{2} - 3 y) - (3 x^{2} + y - x)$ ，其中 $x = - 3 ， y = 2$ ．

(2)、若 $a$ 与 $b$ 互为相反数， $c$ 与 $d$ 互为倒数， $x$ 的绝对值等于5，且 $x > 0$ ，求 $3 (a + b) - 2 c d + x$ 的值．

查看解析
3、计算：

(1)、 $(- 8) + 10 + 2 + (- 1)$ ；

(2)、 $(- 3) - (- 4) \times 3 + (- 16) \div 4$ ；

(3)、 $4 + {(- 2)}^{3} \times 5 - (- 28) \div 4$ ；

(4)、 $2 (a - 2 b) - 3 (2 a - b)$ ；

(5)、 $m - n^{2} - m - n^{2}$ ；

(6)、 $- x + (2 x - 2) - (3 x + 5)$ ．

查看解析
4、下列不是同类项的是（）

A、 $- a b^{3}$ 与 $b^{3} a$ B、12与0 C、 $2 x y z$ 与 $- z y x$ D、 $3 x^{2} y$ 与 $- 6 x y^{2}$

查看解析
5、美丽的东阳是一个充满生机和活力的地域，它古老而又年轻，区内耕地面积约为760000亩，则7600000科学记数法可表示为（）

A、 $76 \times 10^{4}$ B、 $76 \times 10^{5}$ C、 $7.6 \times 10^{6}$ D、 $7.6 \times 10^{4}$

查看解析
6、我国著名数学家华罗庚曾说过“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休．”数学中，数和形是两个最主要的研究对象，它们之间有着十分密切的联系．数形结合是解决数学问题的重要思想方法．如图，已知点 $A$ ， $B$ ， $C$ 在数轴上表示的数分别是1， $- \frac{5}{2}$ ， $- 3$ ，请结合数轴，解答下面的问题：

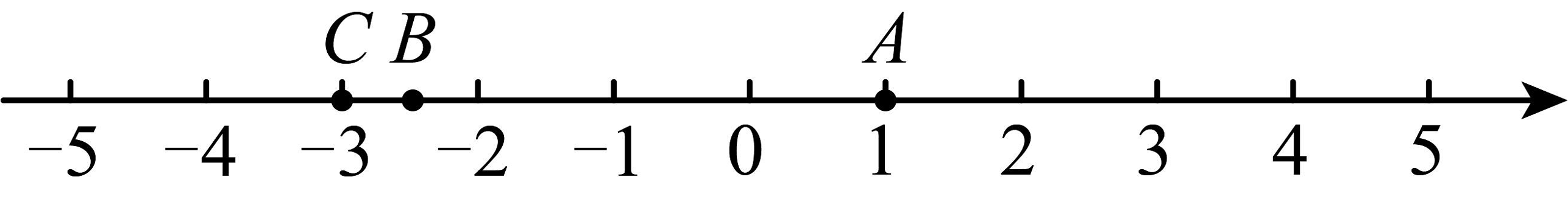(1)、【发现问题】
数轴上，与点 $A$ 的距离为3的点表示的数是．

(2)、【探究问题】
①若将数轴折叠，使得点 $A$ 与点 $C$ 重合，则与点 $B$ 重合的点表示的数是________；
②在①的情况下，若此数轴上 $E$ ， $F$ 两点间的距离为 $2024$ （点 $E$ 在点 $F$ 的左侧），且当点 $A$ 与点 $C$ 重合时，点 $E$ 与点 $F$ 也恰好重合，求 $E$ ， $F$ 两点表示的数．

(3)、【拓展延伸】
已知数轴上 $P$ ， $Q$ 两点间的距离为 $m$ （点 $P$ 在点 $Q$ 的左侧），表示数 $n$ 的点到 $P$ ， $Q$ 两点的距离相等，若将数轴折叠，使得点 $P$ 与点 $Q$ 重合，则 $P$ ， $Q$ 两点表示的数分别是，．（用含 $m$ ， $n$ 的代数式表示）

查看解析
7、为丰富校园体育生活，学校增设羽毛球兴趣小组，需要采购某品牌羽毛球拍 $30$ 支，羽毛球 $x$ 筒（ $x > 30$ ）．经市场调查了解到该品牌羽毛球拍定价 $100$ 元/支，羽毛球 $20$ 元/筒．现甲、乙两家体育用品商店有如下优惠方案：
甲商店：买一支羽毛球拍送一筒羽毛球；
乙商店：羽毛球拍与羽毛球均按九折销售．

(1)、到甲商店购买，需要支付________元；到乙商店购买，需要支付________元．（用含 $x$ 的代数式表示）

(2)、若 $x = 100$ ，请通过计算说明学校去哪个商店购买较为优惠．

(3)、若 $x = 100$ ，你能给出一种更为省钱的购买方案吗？试写出你的购买方案，并算出需要支付的总钱数．

查看解析
8、观察下面三行数：
2， $- 4$ ， 8， $- 16$ ， $32$ ， $- 64$ ， …；①
4， $- 2$ ， $10$ ， $- 14$ ， $34$ ， $- 62$ ， …；②
1， $- 2$ ， 4， $- 8$ ， $16$ ， $- 32$ ， …③

(1)、第①行的第8个数为，第②行的第8个数为，第③行的第8个数为；

(2)、取每行的第 $10$ 个数，计算这三个数的和．

查看解析
9、李阿姨装饰新家，为自己房间的长方形窗户选择了一种遮光的装饰物（如图所示的阴影部分），这种装饰物由一个半圆和两个四分之一圆组成．

(1)、挂上这种装饰物后，窗户能射进阳光的部分的面积是多少？（用含 $a$ ， $b$ 的代数式表示）

(2)、当 $a = 2.5 m$ ， $b = 1 m$ 时，求这扇窗户能射进阳光的部分的面积（ $π$ 取 $3.14$ ）．

查看解析
10、刚大学毕业的小成把自家果园的冬枣放到网上进行直播销售，他原计划每天卖 $100 kg$ 冬枣，但由于种种原因，实际每天的销售量与计划量相比有出入，下表是某周的销售情况（超额记为正，不足记为负）．
星期
一
二
三
四
五
六
日
与计划量的差值/ $kg$
$+ 4$
$- 3$
$- 5$
$+ 14$
$- 8$
$+ 21$
$- 6$

(1)、根据记录的数据可知前三天共卖出冬枣________ $kg$ ；

(2)、若小成将冬枣都按每千克 $14$ 元的价格出售，平均每千克冬枣的运费为6元，不考虑其他成本，求小成这周卖冬枣获得的利润．

查看解析
11、在学习完有理数的运算后，小丽对运算产生了浓厚的兴趣，她借助有理数的运算对有理数 $m$ ， $n$ 定义了一种新运算“※”，规定： $m ※ n = m^{3} - 2 m n + 4 n$ ，例如： $3 ※ 5 = 3^{3} - 2 \times 3 \times 5 + 4 \times 5 = 27 - 30 + 20 = 17$ ．

(1)、求 $2 ※ (- 3)$ 的值；

(2)、求 $[(- 5) ※ 4] - [2 ※ (- \frac{3}{2})]$ 的值．

查看解析
12、有理数 $a$ ， $b$ ， $c$ 在数轴上的位置如图所示，且 $|a| = |c|$ ．

(1)、用“<”连接：（0， $a$ ， $b$ ， $c$ ， $- b$ ）；

(2)、化简： $|a + b| - |a| - |b + c|$ ．

查看解析
13、当 $a = - 2$ ， $b = - \frac{3}{2}$ 时，求下列代数式的值．

(1)、 $a + 2 b$ ；

(2)、 $a^{2} - a b + b^{2}$ ．

查看解析
14、计算：
（1） $- (- 3) - 10 - |- 5| + (- 2)$ ；
（2） $\frac{4}{9} \times (- \frac{7}{12}) \div (- \frac{14}{15})$ ．

查看解析
15、若当 $x = 4$ 时，代数式 $a x^{3} + 2 b x - 1$ 的值是 $2024$ ，则当 $x = - 4$ 时，代数式 $a x^{3} + 2 b x - 1$ 的值是．

查看解析
16、已知 $|a| = 2$ ， $|b + 3| = 2$ ，且 $a < b$ ，则 $a - b$ 的值为．

查看解析
17、某蓄水池的标准水位记为 $0 m$ ，若 $+ 0.09 m$ 表示水面高于标准水位 $0.09 m$ ，则水面低于标准水位 $0.03 m$ ，可记为 $m$ ．

查看解析
18、我们知道，用字母表示的代数式是具有一般意义的．下列赋予 $4 a$ 实际意义的例子中，不正确的是（）

A、若某款笔记本的售价是4元/本，则 $4 a$ 表示购买 $a$ 本笔记本所需的钱数 B、若 $a$ 表示一个正方形的边长，则 $4 a$ 表示这个正方形的周长 C、若某校七年级共有4个班，平均每个班有 $a$ 名女生，则 $4 a$ 表示该校七年级女生的总人数 D、若4和 $a$ 分别表示一个两位数的十位上的数字和个位上的数字，则 $4 a$ 表示这个两位数

查看解析
19、已知有理数 $a$ ， $b$ 在数轴上的位置如图所示，则下列结论错误的是（）

A、 $a < 1 < b$ B、 $a b > 0$ C、 $a + b > 0$ D、 $a - b < 0$

查看解析
20、已知摄氏温度（ $°C$ ）与华氏温度（ $°F$ ）之间的转换关系是： $t_{c} = \frac{5}{9} (t_{F} - 32)$ 或 $t_{F} = \frac{9}{5} t_{c} + 32$ （ $t_{c}$ 表示摄氏度数， $t p$ 表示华氏度数）．某天某市的最高气温是 $20 °C$ ，则这一天该市的最高气温用华氏温度表示是（）

A、 $- 4 °F$ B、 $- \frac{20}{3} °F$ C、 $\frac{260}{9} °F$ D、 $68 ° F$

查看解析

上一页 833 834 835 836 837 下一页跳转

星期	一	二	三	四	五	六	日
与计划量的差值/ $kg$	$+ 4$	$- 3$	$- 5$	$+ 14$	$- 8$	$+ 21$	$- 6$