相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、我们知道,任意一个正整数都可以进行这样的分解:( , 是正整数,且),在的所有这种分解中,如果 , 两因数之差的绝对值最小,我们就称是的最佳分解,并规定: . 例如:12可以分解成 , 或 , 因为 , 所以是12的最佳分解,所以 . 如果一个两位正整数 , ( , , 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为 , 那么我们称这个数为“吉祥数”.根据以上新定义,下列说法正确的有:( )
(1);(2)和是“吉祥数”;(3)“吉祥数”中,的最小值为;(4)如果一个正整数是另外一个正整数的平方,我们称正整数是完全平方数,则对任意一个完全平方数 , 总有;
A、1个 B、2个 C、3个 D、4个 -
2、若 , , 则的值为( )A、0 B、2 C、3 D、4
-
3、已知是一个完全平方式,则的值是( )A、5 B、9或 C、 D、
-
4、下列运算:①;②;③;④ . 其中,运算正确的有( )A、1个 B、2个 C、3个 D、4个
-
5、在 , , , , , , (在相邻两个2之间1的个数逐次加1)中,无理数的个数为( )A、5 B、2 C、3 D、4
-
6、在矩形中,E是边上一点,连接 , 将沿翻折得到 .
 (1)、如图1,若 , 当点F在矩形对角线上时,求的长;(2)、如图2,当点F在上时,若 , 求的长;(3)、如图3,若 , 延长 , 与的平分线交于点G,交于点,求的值.
(1)、如图1,若 , 当点F在矩形对角线上时,求的长;(2)、如图2,当点F在上时,若 , 求的长;(3)、如图3,若 , 延长 , 与的平分线交于点G,交于点,求的值. -
7、如图,在平面直角坐标系中,直线与x轴,y轴分别交于A, B两点,直线与x轴,y轴分别交于C,D两点,这两条直线相交于点P.
 (1)、求点P的坐标;(2)、在坐标平面内是否存在一点Q,使以A,P,D,Q为顶点的四边形是菱形?若存在,请求出点Q的坐标,若不存在,请说明理由;(3)、在x轴上是否存在一点M,使?若存在,请求出点M的坐标,若不存在,请说明理由.
(1)、求点P的坐标;(2)、在坐标平面内是否存在一点Q,使以A,P,D,Q为顶点的四边形是菱形?若存在,请求出点Q的坐标,若不存在,请说明理由;(3)、在x轴上是否存在一点M,使?若存在,请求出点M的坐标,若不存在,请说明理由. -
8、如图,P是的边的延长线上任意一点,分别交和于点M和N.
 (1)、若 , 求的值;(2)、求证: .
(1)、若 , 求的值;(2)、求证: . -
9、如图,点E为正方形对角线上一点,连接 , . 过点E作 , 交边于点F,以 , 为邻边作矩形 .
 (1)、求证:矩形是正方形;(2)、连接 , 若正方形的边长为9, , 求正方形的边长.
(1)、求证:矩形是正方形;(2)、连接 , 若正方形的边长为9, , 求正方形的边长. -
10、如图,在平面直角坐标系内,的三个顶点坐标分别为 , , .
 (1)、画出关于y轴对称的;(2)、在第四象限画出以点O为位似中心的位似图形 , 与的位似比为;(3)、求以 , , , 四个点为顶点构成的四边形的面积.
(1)、画出关于y轴对称的;(2)、在第四象限画出以点O为位似中心的位似图形 , 与的位似比为;(3)、求以 , , , 四个点为顶点构成的四边形的面积. -
11、如图,是由7个大小相同的小立方体块搭建的几何体,其中每个小正方体的棱长为2厘米.
 (1)、请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图;(2)、直接写出这个几何体的表面积(包括底部):__________.
(1)、请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图;(2)、直接写出这个几何体的表面积(包括底部):__________. -
12、用适当方法解下列方程:(1)、(2)、
-
13、若是方程的根,则的值为 .
-
14、已知 , 则的值为 .
-
15、如图,在边长为的菱形中, , 是边上的动点,是边上的动点,且 , 连接 , 则的最小值是( ) .
 A、3 B、6 C、 D、
A、3 B、6 C、 D、 -
16、如图,菱形的对角线 , 相交于点O,过点D作于点H,连接 , , 若菱形的面积为16,则的长为( )
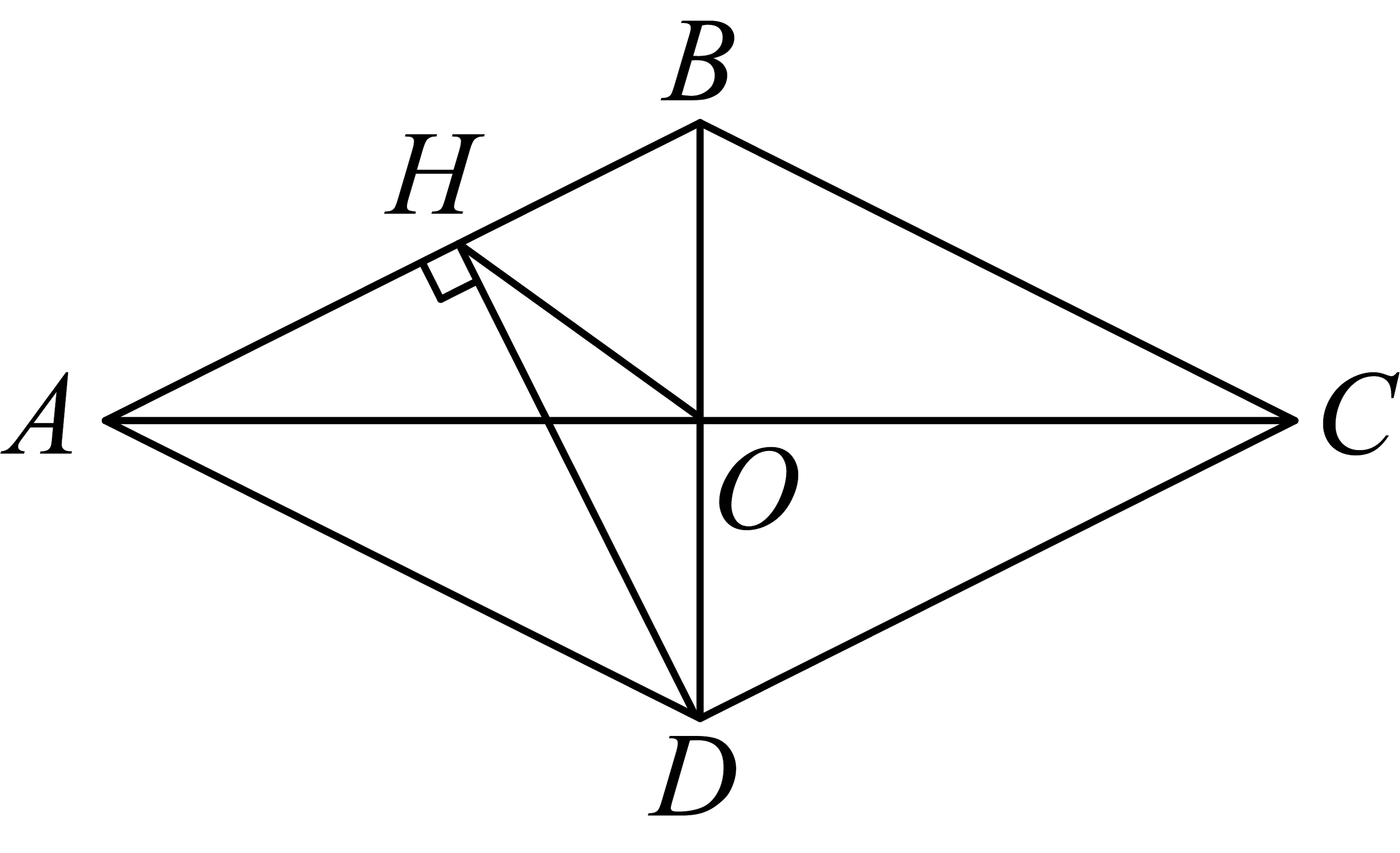 A、4 B、 C、8 D、
A、4 B、 C、8 D、 -
17、天坛是古代帝王祭天的地方,其中最主要的建筑就是祈年殿.老师希望同学们利用所学过的知识测量祈年殿的高度,数学兴趣小组的同学们设计了如图所示的测量图形,并测出竹竿长2米,在太阳光下,它的影长为米,同一时刻,祈年殿的影长约为米.请你根据这些数据计算出祈年殿的高度约( )米.
 A、20 B、15 C、28 D、38
A、20 B、15 C、28 D、38 -
18、一元二次方程的二次项系数、一次项系数、常数项分别是( )A、 B、 C、 D、
-
19、
概率学习
规定:求若干个相同的有理数(均不等于的除法运算叫做除方,如 , 等.类比有理数的乘方,我们把记作 , 读作“2的圈3次方”, 记作 , 读作“的圈4次方”.
初步探究
(1)直接写出计算结果: 、 ;(2)关于除方,下列说法错误的是 .A. 任何非零数的圈2次方都等于1;
B. 对于任何正整数n,1的圈n次方都等于1;
C. ;
D. 负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.
深入思考:
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算
(3)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.的圈4次方 ;
的圈6次方 ;
(4)想一想:将一个非零有理数a的圈n次方写成幂的形式= ;(5)算一算: .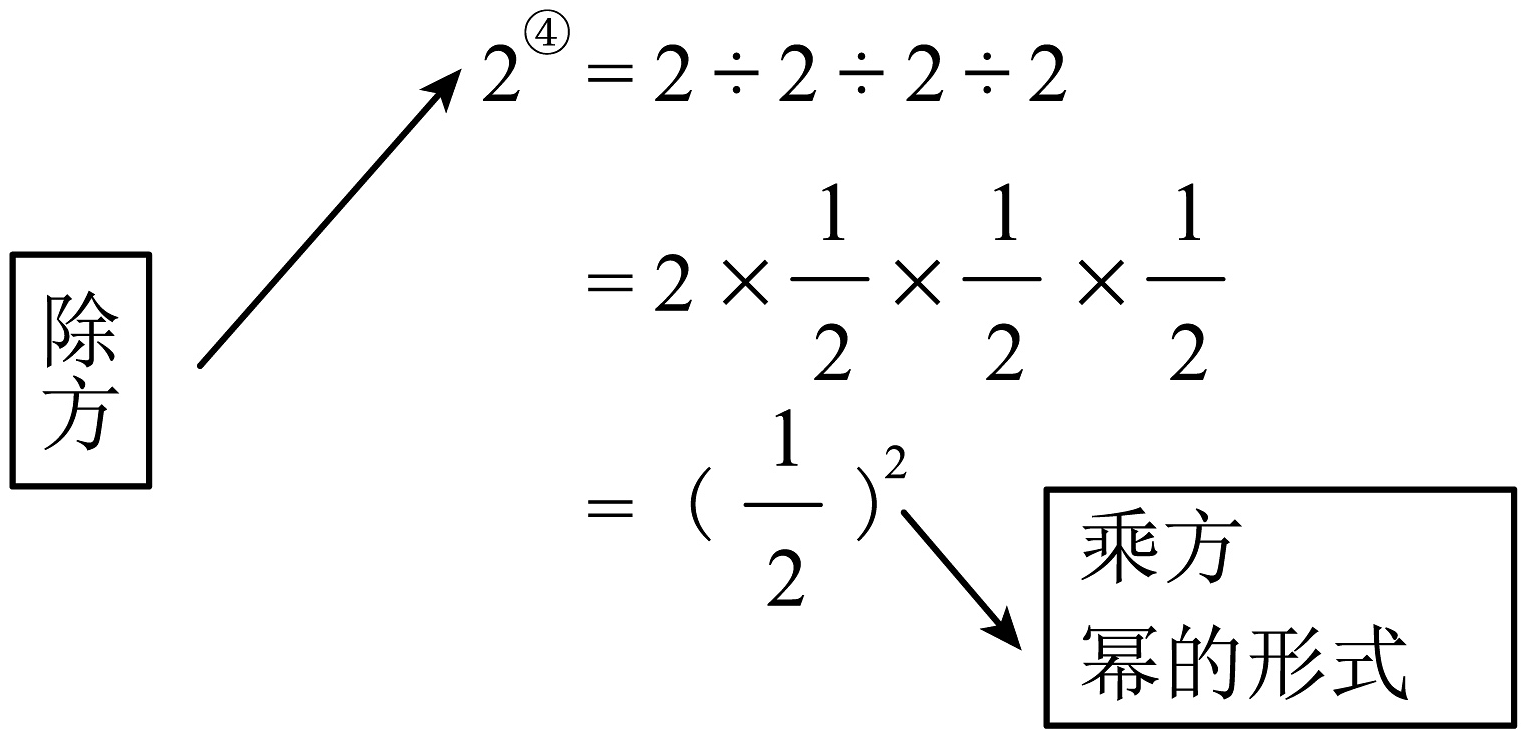
-
20、在学习绝对值时,老师教过我们绝对值的几何含义,表示5在数轴上对应的点到原点的距离,可以表示为:;那么表示在数轴上对应的两点之间的距离; , 所以表示在数轴上对应的两点之间的距离.(1)、若 , 则_______, ________;(2)、若 , 则_______;(3)、若 , 且x的值为整数,则x值为_______;