相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、解方程(1)、;(2)、 .
-
2、计算(1)、;(2)、;(3)、 .
-
3、如图, , 过点A作直线 , 点B在直线l上, , 以点O为圆心,以长为半径作弧,与的延长线交于点C,则点C表示的实数是 .

-
4、如图,△ABD≌△CAE,若BD=4cm,CE=3cm,则DE=cm.

-
5、与最简二次根式是同类二次根式,则 .
-
6、的相反数是 , 绝对值是 .
-
7、如图,一只蚂蚁从长宽高分别是3,2,6的长方体纸箱的A点沿纸箱表面爬到B点,那么它所行的最短路线的长是( ).
 A、 B、11 C、7 D、8
A、 B、11 C、7 D、8 -
8、如图,数轴上点P表示的数可能是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
9、在﹣与之间的整数是( )A、﹣2,﹣1,0,1,2,3 B、﹣2,﹣1,0,1,2 C、﹣1,0,1,2,3 D、﹣1,0,1,2
-
10、以下三个数,不能组成直角三角形的是( )A、2,3,4 B、5,12,13 C、3,4,5 D、7,24,25
-
11、图中字母A所代表的正方形的面积是( ).
 A、175 B、225 C、400 D、625
A、175 B、225 C、400 D、625 -
12、实数 , , , , 中,无理数的个数是( )A、2个 B、3个 C、4个 D、5个
-
13、下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、
-
14、36的算术平方根是( ).A、 B、-6 C、6 D、36
-
15、为响应国家“乡村振兴”的号召,建设绿色生态农村,王大爷承包了一片土地用于种植某品种草莓.如图所示是种植草莓的土地平面示意图(单位:米)
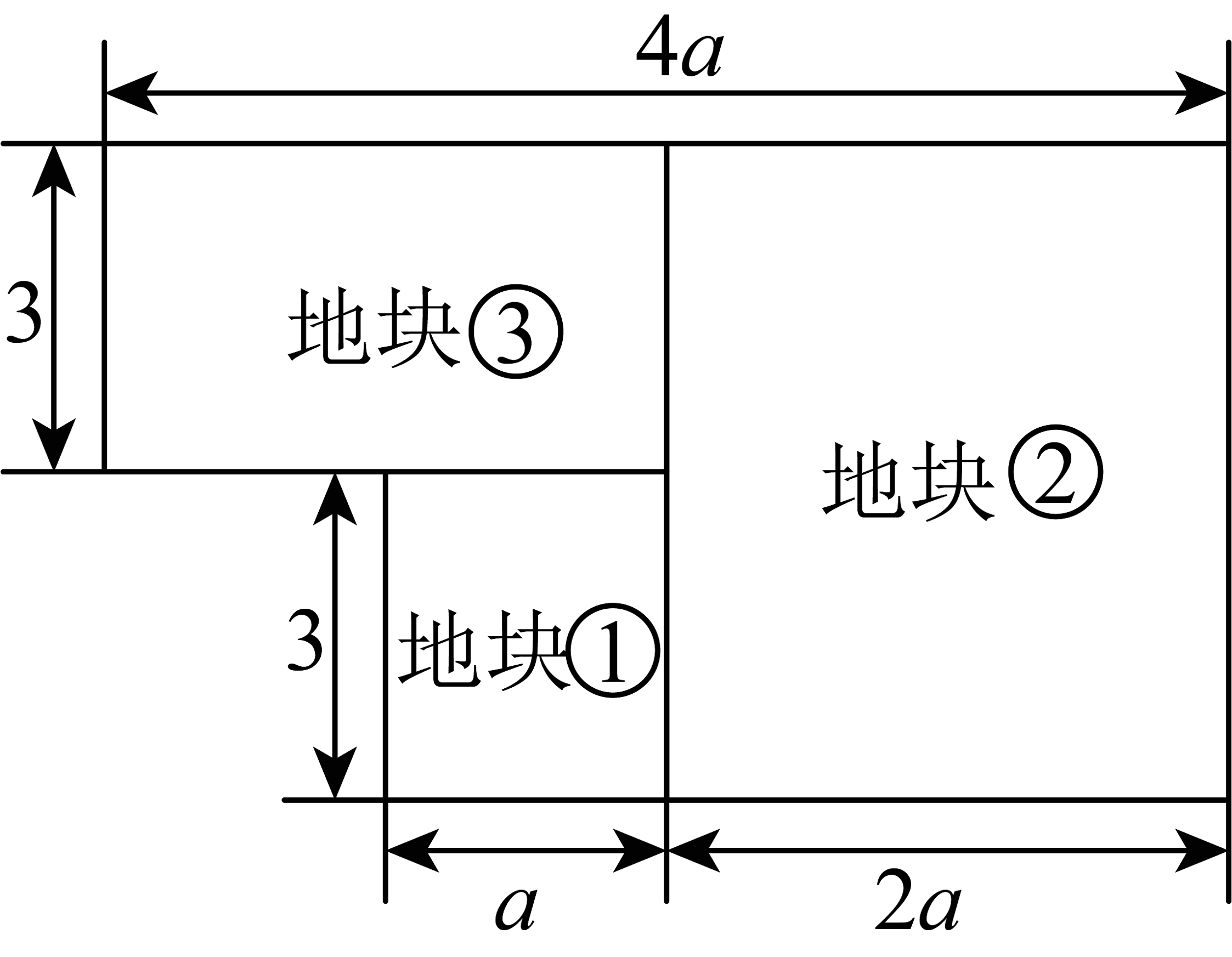 (1)、用含的式子表示出这片土地的总面积;(2)、由于草莓品种和各个地块土壤条件存在差异,地块②平均每平方米可种植2株草莓,剩下地块平均每平方米可种植3株草莓,则当时,王大爷承包的土地一共可以种植多少株草莓?
(1)、用含的式子表示出这片土地的总面积;(2)、由于草莓品种和各个地块土壤条件存在差异,地块②平均每平方米可种植2株草莓,剩下地块平均每平方米可种植3株草莓,则当时,王大爷承包的土地一共可以种植多少株草莓? -
16、已知有理数所表示的点到原点的距离为个单位长度,互为相反数且都不为零,互为倒数.(1)、求的值.(2)、求的值.
-
17、化简求值:的值,其中 .
-
18、计算: .
-
19、将下列各数填入相应的大括号内(无需化简,原式填入):
, , , , , , ,
整数集合:{ };
正有理数集合:{ };
非负整数集合:{ };
负分数集合:{ }.
-
20、一个正方体的表面展开图如图所示,六个面上各有一字,连起来的意思是“爱大沥讲文明”,把它折成正方体后,与“大”相对的字是( )
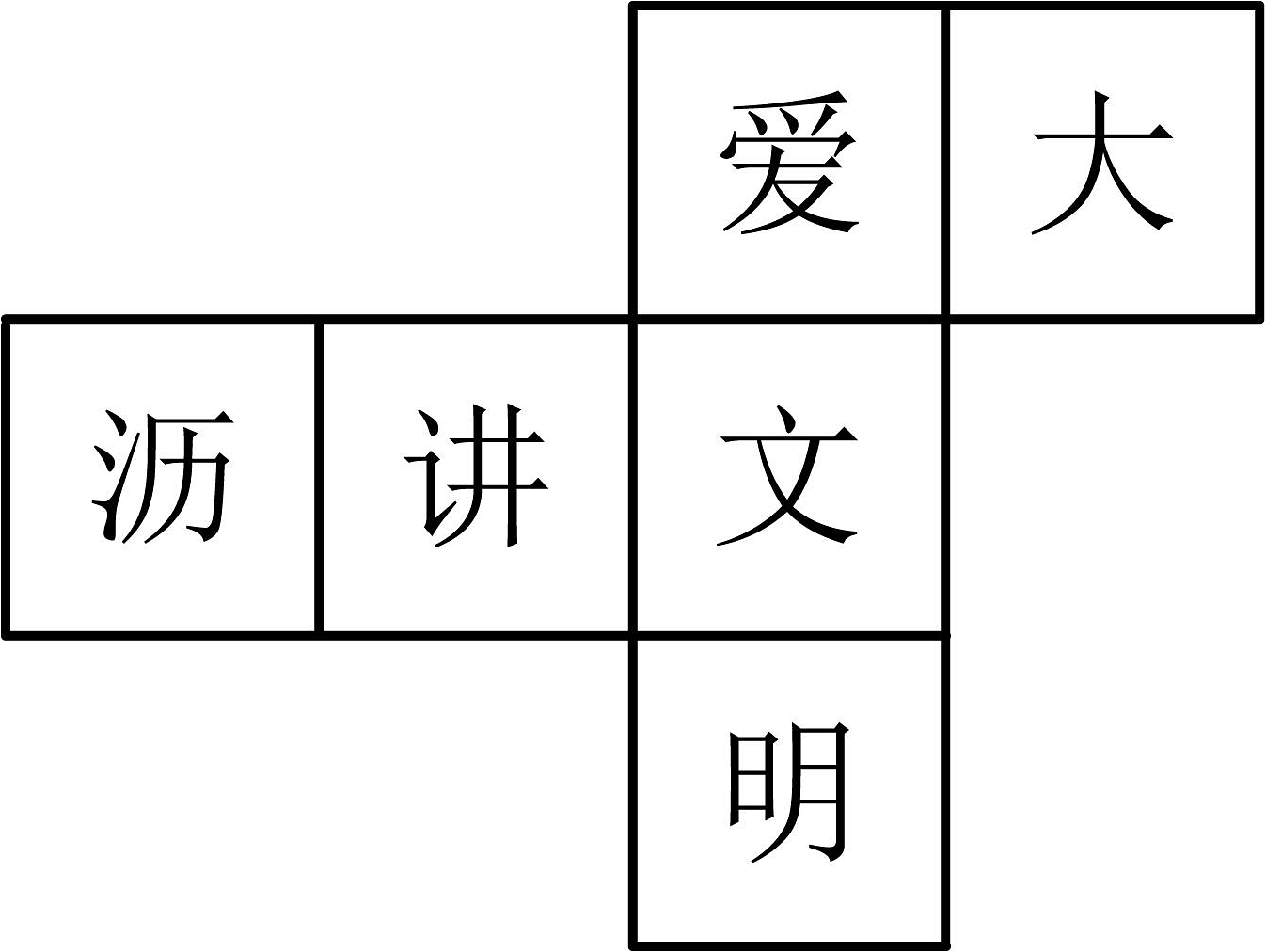 A、沥 B、讲 C、文 D、明
A、沥 B、讲 C、文 D、明