相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、如图,已知数轴上两点对应的数分别为、 , 点P为数轴上一动点,其对应的数为x.
 (1)、(填空)若点P从B开始向左移动6个单位长度,则______.若点P向左移动到与点A距离3个单位长度时,则点P对应的数是______.(2)、(填空)当点P从点B以每秒3个单位长度的速度向右移动,则t秒后P点表示的数是______,此时若将数轴折叠,使与3表示的点重合,则点P与数______表示的点重合(用含t的式子表示);(3)、若点P从A点出发沿数轴的负方向移动,速度为每秒1个单位长度,同时点Q从B出发同向移动,速度为每秒3个单位长度,设运动时间为t,在移动过程中,是否存在某一时刻t,使得点Q与点P之间的距离等于2个单位长度,若存在,请求出t的值;若不存在,请说明理由.
(1)、(填空)若点P从B开始向左移动6个单位长度,则______.若点P向左移动到与点A距离3个单位长度时,则点P对应的数是______.(2)、(填空)当点P从点B以每秒3个单位长度的速度向右移动,则t秒后P点表示的数是______,此时若将数轴折叠,使与3表示的点重合,则点P与数______表示的点重合(用含t的式子表示);(3)、若点P从A点出发沿数轴的负方向移动,速度为每秒1个单位长度,同时点Q从B出发同向移动,速度为每秒3个单位长度,设运动时间为t,在移动过程中,是否存在某一时刻t,使得点Q与点P之间的距离等于2个单位长度,若存在,请求出t的值;若不存在,请说明理由. -
2、理解与思考:整体代换是数学的一种思想方法.例如:若 , 则;我们将作为一个整体代入,则原式 . 咱仿照上面的解题方法,完成下面的问题:(1)、若 , 求的值:(2)、若 , 求的值.
-
3、先化简,再求值: , 其中 .
-
4、为任何非零有理数,则的值是 .
-
5、若互为相反数,互为倒数,c的绝对值等于2,则 .
-
6、在中国明代的《算法统宗》一书中将用格子的方法计算两个数相乘称作“铺地锦”,如图1,计算 , 将乘数记入格子上面,乘数记入格子右侧,然后用乘数的每位数字乘以乘数的每位数字,将结果记入相应的格子中,最后按斜行加起来,得到 . 如图2,用“铺地锦”的方法表示两位数相乘,下列结论正确的个数有( )

①b的值为5 ②a为偶数
③乘积结果可以表示为 ④a的值为1
A、1个 B、2个 C、3个 D、4个 -
7、如图,在一个长方形中放入三个正方形,从大到小正方形的边长分别为、、 , 则右上角阴影部分的周长与左下角阴影部分周长差为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8、定义一种新运算: , 如则的值( )A、 B、0 C、 D、4
-
9、有理数、在数轴上的位置如图所示,下列结论:;;; , 其中正确的个数是( )
 A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个 -
10、下列说法正确的是( )A、系数是 , 次数是 B、是负数 C、和的结果相等 D、多项式是二次三项式
-
11、下列各数中,正数有( )A、2个 B、3个 C、4个 D、5个
-
12、下列计算结果正确的是( )A、 B、 C、 D、
-
13、电影《志愿军:存亡之战》备受观众喜爱,截止到年月初,累计票房亿元,亿元用科学记数法表示为( )A、元 B、元 C、元 D、元
-
14、如图所示的是某用户支付宝的账单截图,其中表示的意思是( )
 A、收入100元 B、支出100元 C、余额100元 D、存款100元
A、收入100元 B、支出100元 C、余额100元 D、存款100元 -
15、如图,在中, , . 过点的射线交边于点 , 于点 , 于点 , , .
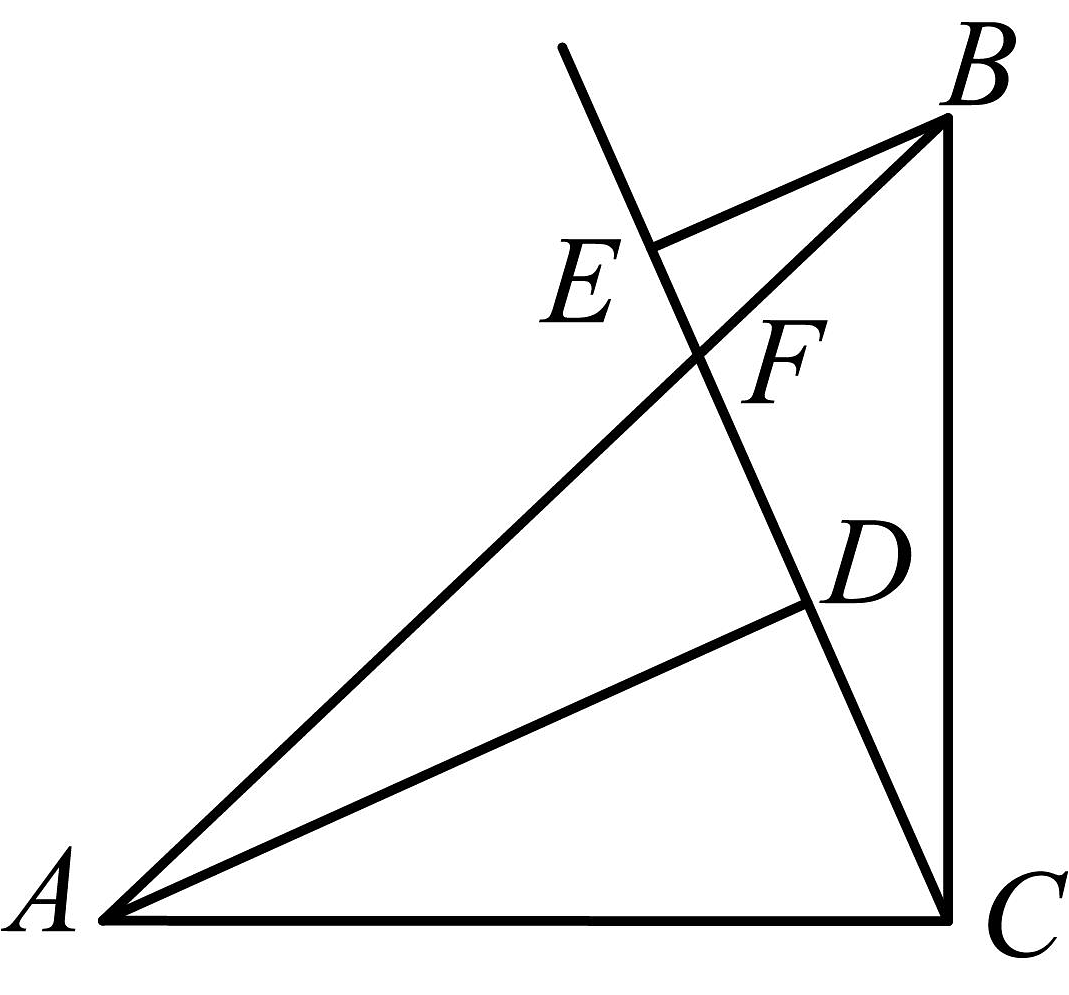
(1)求证:;
(2)求的长.
-
16、化简与求值:(1)、化简:;(2)、化简求值: , 其中 .
-
17、计算:(1)、;(2)、 .
-
18、“山高水阔知何处?巧构全等觅飞痕”如图所示,两条互相垂直的数轴相交于 , 点在右侧个单位长度处,点是下方轴上一动点,连接 , 过点作 , 若 , 点在左侧轴上个单位长度处,连接 , 的最小值为个单位长度.

-
19、如图,相交于点O,已知 , 要直接根据“”证明 , 还要添加一个条件是 .

-
20、已知 , 则代数式值为 .