相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、与的和为( )A、 B、 C、8 D、2
-
2、如图所示,和都是等边三角形,且、、在同一直线上,连接交于 , 连接交于 , 连接 . 求证:
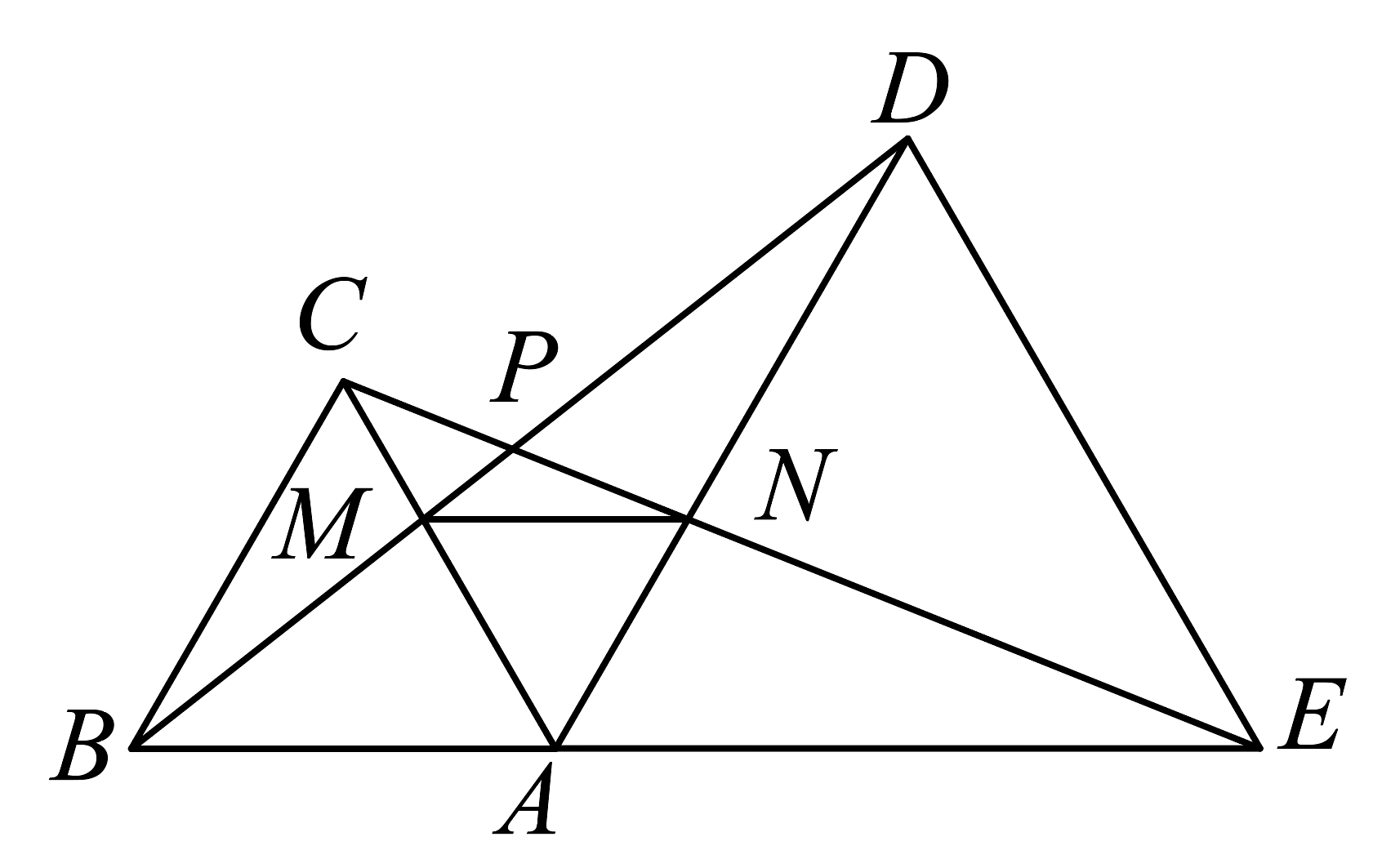 (1)、;(2)、的度数;(3)、判断的形状,并说明理由.
(1)、;(2)、的度数;(3)、判断的形状,并说明理由. -
3、如图,某小区有一块长为米,宽为米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
 (1)、用含有的式子表示绿化的总面积(结果写成最简形式);(2)、当 , , 求绿化的总面积;(3)、在()的条件下,开发商找来甲、乙两绿化队完成此项任务.已知甲队每小时可绿化平方米,乙队每小时绿化平方米,若根据施工队的工期需要,甲队的工作时间比乙队的工作时间少小时,则甲、乙两队各工作多少小时?
(1)、用含有的式子表示绿化的总面积(结果写成最简形式);(2)、当 , , 求绿化的总面积;(3)、在()的条件下,开发商找来甲、乙两绿化队完成此项任务.已知甲队每小时可绿化平方米,乙队每小时绿化平方米,若根据施工队的工期需要,甲队的工作时间比乙队的工作时间少小时,则甲、乙两队各工作多少小时? -
4、如图,于 , 于 , 平分 , .
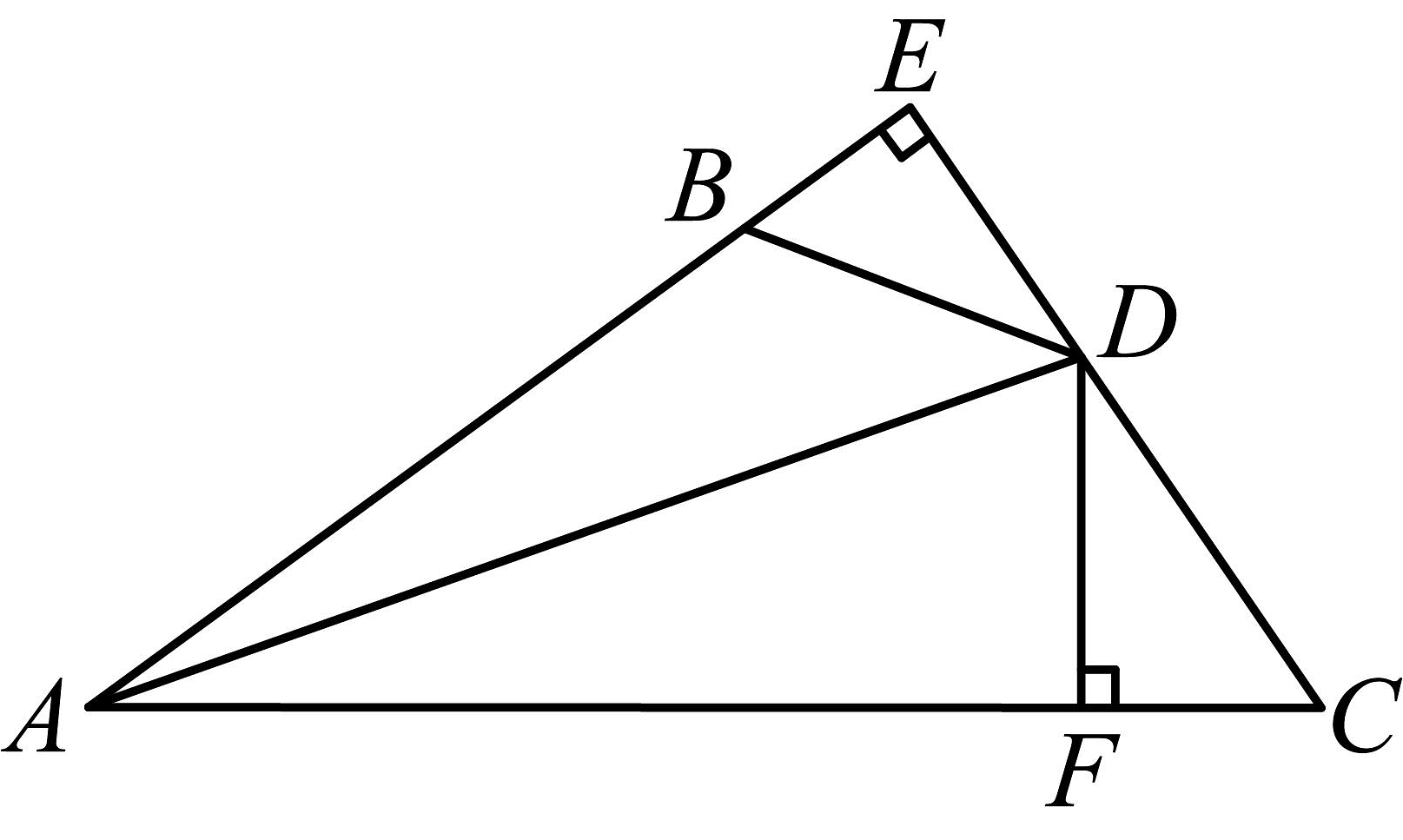 (1)、求证:;(2)、已知 , . 求的面积.
(1)、求证:;(2)、已知 , . 求的面积. -
5、如图,点A,C,B,D在一条直线上, , , . 求证: .

-
6、先化简,再求值: , 其中 .
-
7、计算: .
-
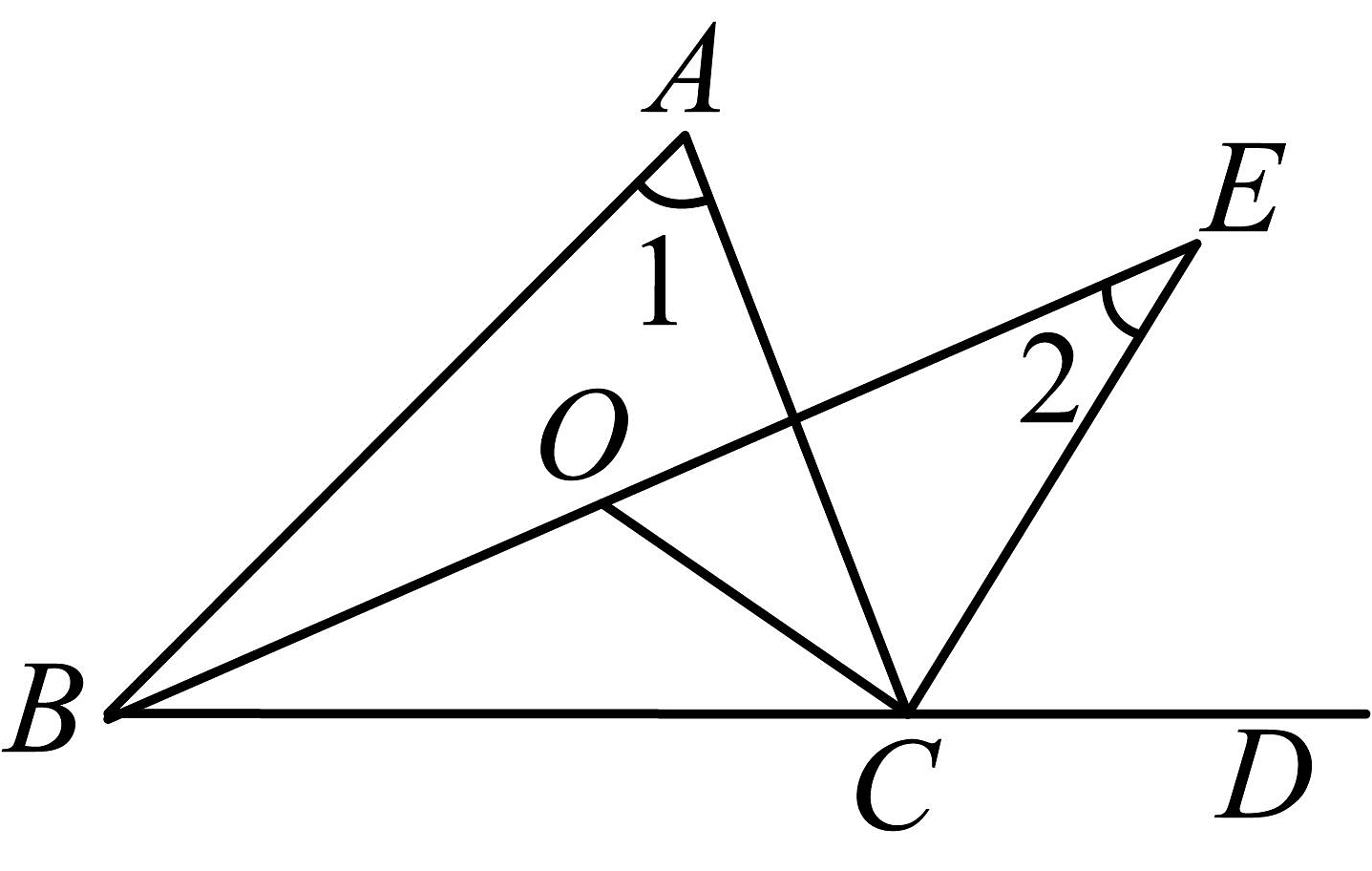
8、如图,在中, , 的平分线 , 交于点 , 为的外角的平分线,的延长线交于点 , , 则的大小为
-
9、如图,中, , 若沿图中虚线截去 , 则 .

-
10、 .
-
11、计算: .
-
12、若 , , 则( )A、150 B、160 C、165 D、180
-
13、下列各组长度的线段能构成三角形的是( )A、1,2,4 B、3,4,7 C、4,4,10 D、3,4,5
-
14、的倒数是( )A、 B、2025 C、 D、
-
15、如图所示,在长为 , 宽为的矩形中,截去一个矩形(图中阴影部外),如果剩下的矩形与原矩形相似,那么截去矩形的面积是 .

-
16、我国三国时期的数学家赵爽(公元2~3世纪)研究过某类一元二次方程的正数解的几何解法.以方程 , 即为例说明,他在其所著的《勾股圆方图注》中记载的方法是:构造如图所示的大正方形,它的面积可表示为 , 同时也可以表示为四个矩形的面积加上中间小正方形的面积,即 , 因此有 , 可得方程的正数解为 . 小明用此方法解关于的方程时,构造出类似的图形,如果大正方形的面积为41,小正方形的面积为9,则的值分别为( )
 A、2,8 B、3,8 C、2,9 D、3,9
A、2,8 B、3,8 C、2,9 D、3,9 -
17、下列长度的两条线段与长度为12的线段首尾依次相连能组成直角形三角形的是( )A、6,9 B、9,15 C、10,16 D、15,18
-
18、的结果为( )A、3 B、 C、 D、9
-
19、9的算术平方根是( )A、 B、3 C、 D、81
-
20、已知,在四边形中, , , 分别是边上的点.且 . 探究线段的数量关系.
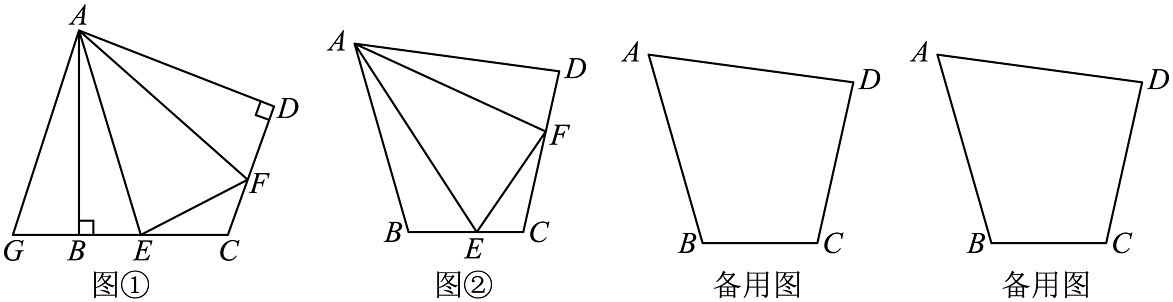 (1)、为探究上述问题,小宁先画出了其中一种特殊情况,如图①当 , 小宁探究此问题的方法是:延长到点 , 使 , 连接 , 请你补全小宁的解题思路:先证明________;再证明_________;即可得出线段之间的数量关系是______________________.(2)、如图②,在四边形中, , , 分别是边上的点,且 , (1)中的结论是否仍然成立?请写出证明过程;(3)、在四边形中, , , 分别是所在直线上的点,且 . 请直接写出线段之间的数量关系.
(1)、为探究上述问题,小宁先画出了其中一种特殊情况,如图①当 , 小宁探究此问题的方法是:延长到点 , 使 , 连接 , 请你补全小宁的解题思路:先证明________;再证明_________;即可得出线段之间的数量关系是______________________.(2)、如图②,在四边形中, , , 分别是边上的点,且 , (1)中的结论是否仍然成立?请写出证明过程;(3)、在四边形中, , , 分别是所在直线上的点,且 . 请直接写出线段之间的数量关系.