相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、对称美是我国古代平衡思想的体现,常用于标识的设计上,使对称美惊艳了千年时光.下列校徽图标是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
2、 图形的性质(1)、成轴 对 称 的 两 个 图 形,对应 线 段 , 对应角 , 对称轴是连结两个对称点的线段的垂直平分线;(2)、成中心对称的两个图形,对应线段 , 对应角相等,连结两个对称点的线段都经过且被对称中心.
-
3、轴对称与中心对称(1)、轴对称是一个图形沿某直线翻折后,能和图形互相重合;(2)、中心对称是一个图形绕某一点旋转后,能和另一个图形互相重合.
-
4、轴对称图形与中心对称图形(1)、如果把一个图形沿着一条直线折叠后,直线两侧的部分能够 , 那么这个图形叫做轴对称图形;(2)、如果一个图形绕着一个点旋转后,能够和原来的图形互相重合,那么这个图形叫做中心对称图形,这个那点叫.
-
5、(2023 温州)如图,在 2×4 的方格纸ABCD中,每个小方格的边长均为1.已知格点P,请按要求画格点三角形(顶点均在格点上).
 (1)、在图①中画一个等腰三角形 PEF,使底边长为 , 点E在BC上,点 F在AD上,再画出该三角形绕矩形ABCD的中心旋转180°后的图形;(2)、在图②中画一个 Rt△PQR,使∠P=45°,点Q在BC上,点R在AD 上,再画出该三角形向右平移1个单位后的图形.
(1)、在图①中画一个等腰三角形 PEF,使底边长为 , 点E在BC上,点 F在AD上,再画出该三角形绕矩形ABCD的中心旋转180°后的图形;(2)、在图②中画一个 Rt△PQR,使∠P=45°,点Q在BC上,点R在AD 上,再画出该三角形向右平移1个单位后的图形. -
6、如图,在 6×6 的正方形网格中,△ABC的顶点在格点上,仅用无刻度的直尺按要求在网格中作图.
 (1)、在图①中画出线段AD,点 D在BC 上,使得S△ACD : S△ABD=1: 2;(2)、在图②中画出△ABC的重心E.
(1)、在图①中画出线段AD,点 D在BC 上,使得S△ACD : S△ABD=1: 2;(2)、在图②中画出△ABC的重心E. -
7、尺规作图问题:
如图①,E 是▱ABCD 边 AD 上一点(不包含点 A,D),连结CE.用尺规作 AF∥CE,F是边BC 上一点.
小明:如图②,以点C为圆心,AE长为半径作弧,交 BC于点 F,连结AF,则AF∥CE.
小丽:以点 A 为圆心,CE 长为半径作弧,交BC于点F,连结AF,则AF∥CE.
小明:小丽,你的作法有问题.
小丽:哦……我明白了!
 (1)、证明小明的作法中AF∥CE;(2)、指出小丽作法中存在的问题.
(1)、证明小明的作法中AF∥CE;(2)、指出小丽作法中存在的问题. -
8、利用尺规作图在一个矩形内作菱形ABCD,则下列作法中错误的是( )A、
 B、
B、 C、
C、 D、
D、
-
9、在学完《切线的性质与判定》后,王老师布置以下一道题:如图所示,已知⊙O及⊙O外一点 P.
 (1)、按要求完成作图步骤并准确标注字母.尺规作图:作出线段OP 的垂直平分线交OP 于点A;以点 A为圆心,AP 为半径作⊙A,⊙A与⊙O交于点B(点B位于直线OP 上方),连结 PB.(2)、(1)中作图得到的 PB 是⊙O 的切线吗?请说明理由.(3)、设(1)中所作垂直平分线交BP于点C,若⊙O的半径为3,CP=5,求OP 的长.
(1)、按要求完成作图步骤并准确标注字母.尺规作图:作出线段OP 的垂直平分线交OP 于点A;以点 A为圆心,AP 为半径作⊙A,⊙A与⊙O交于点B(点B位于直线OP 上方),连结 PB.(2)、(1)中作图得到的 PB 是⊙O 的切线吗?请说明理由.(3)、设(1)中所作垂直平分线交BP于点C,若⊙O的半径为3,CP=5,求OP 的长. -
10、如图,过直线AB 外的点 P作直线 AB 的平行线,图29-19中作法错误的是( )
 A、
A、 B、
B、 C、
C、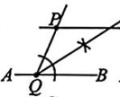 D、
D、
-
11、下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.
已知:如图①,直线l和直线l外一点 P.

求作:直线l的平行线,使它经过点 P.
作法:如图②,
①过点 P 作直线m 与直线l 交于点O;
②在直线m上取一点A(OA<OP),以点O为圆心,OA 长为半径画弧,与直线l交于点 B;
③以点 P 为圆心,OA 长为半径画弧,交直线m于点C(点C在点 P 的右侧),以点 C为圆心,AB长为半径画弧,两弧交于点 D;
④作直线 PD.
直线 PD 就是所求作的直线.
(1)、依作法补全图形;(2)、该作图的依据是. -
12、尺规作图:
 (1)、如图①,作三角形的外接圆;(2)、如图②,作三角形的内切圆.
(1)、如图①,作三角形的外接圆;(2)、如图②,作三角形的内切圆. -
13、 如图4,已知:∠α,直线l及l上两点A,B.求作:Rt△ABC,使点 C 在直线l 的上方,且∠ABC=90°,∠BAC=∠α.

-
14、如图,在△ABC中,分别以点A,B为圆心,大于 AB 的长为半径画弧,两弧交于点 E,F,作直线 EF 分别交BC,AB 于点 D,M,连结 AD.若AC=4,CD=3,AD=5,则AB的长为( )
 A、5 B、4 C、9 D、10
A、5 B、4 C、9 D、10 -
15、如图,在△ABC中,AB=AC,∠A=100°,进行如下操作:①以点 B 为圆心,小于AB的长为半径作弧,分别交BA,BC于点E,F;②分别以点E,F为圆心,大于 EF的长为半径作弧,两弧交于点 M;③作射线 BM交AC 于点 D,则∠BDC 的度数为°.

-
16、如图,在△ABC中,∠C=90°,用直尺和圆规在边 BC 上确定一点 P,使点 P 到边 AC,AB 的距离相等,则符合要求的作图痕迹是( )A、
 B、
B、 C、
C、 D、
D、
-
17、如图,用尺规作“与已知角相等的角”的过程中,作出. 的依据是( )
 A、SAS B、ASA C、AAS D、SSS
A、SAS B、ASA C、AAS D、SSS -
18、实际问题:
某商场为鼓励消费,设计了投资活动.方案如下:根据不同的消费金额,每次抽奖时可以从100张面值分别为1元、2元、3元、…、100元的奖券中(面值为整数),一次任意抽取2张、3张、4张、…等若干张奖券,奖券的面值金额之和即为优惠金额.某顾客获得了一次抽取5张奖券的机会,小明想知道该顾客共有多少种不同的优惠金额?
问题建模:
从1,2,3,…,(为整数,且)这个整数中任取个整数,这个整数之和共有多少种不同的结果?
模型探究:
我们采取一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,从中找出解决问题的方法.
探究一:
(1)从1,2,3这3个整数中任取2个整数,这2个整数之和共有多少种不同的结果?
表①
所取的2个整数
1,2
1,3,
2,3
2个整数之和
3
4
5
如表①,所取的2个整数之和可以为3,4,5,也就是从3到5的连续整数,其中最小是3,最大是5,所以共有3种不同的结果.
(2)从1,2,3,4这4个整数中任取2个整数,这2个整数之和共有多少种不同的结果?
表②
所取的2个整数
1,2
1,3,
1,4
2,3
2,4
3,4
2个整数之和
3
4
5
5
6
7
如表②,所取的2个整数之和可以为3,4,5,6,7,也就是从3到7的连续整数,其中最小是3,最大是7,所以共有5种不同的结果.
(3)从1,2,3,4,5这5个整数中任取2个整数,这2个整数之和共有______种不同的结果.
(4)从1,2,3,…,(为整数,且)这个整数中任取2个整数,这2个整数之和共有______种不同的结果.
探究二:
(1)从1,2,3,4这4个整数中任取3个整数,这3个整数之和共有______种不同的结果.
(2)从1,2,3,…,(为整数,且)这个整数中任取3个整数,这3个整数之和共有______种不同的结果.
探究三:
从1,2,3,…,(为整数,且)这个整数中任取4个整数,这4个整数之和共有______种不同的结果.
归纳结论:
从1,2,3,…,(为整数,且)这个整数中任取个整数,这个整数之和共有______种不同的结果.
问题解决:
从100张面值分别为1元、2元、3元、…、100元的奖券中(面值为整数),一次任意抽取5张奖券,共有______种不同的优惠金额.
拓展延伸:
(1)从1,2,3,…,36这36个整数中任取多少个整数,使得取出的这些整数之和共有204种不同的结果?(写出解答过程)
(2)从3,4,5,…,(为整数,且)这个整数中任取个整数,这个整数之和共有______种不同的结果.
-
19、如图,在平面直角坐标系xOy中,正方形ABCD的边AB在x轴的正半轴上,顶点C,D在第一象限内,正比例函数y1=3x的图象经过点D,反比例函数的图象经过点D,且与边BC交于点E,连接OE,已知AB=3.
(1)点D的坐标是 ;
(2)求tan∠EOB的值;
(3)观察图象,请直接写出满足y2>3的x的取值范围;
(4)连接DE,在x轴上取一点P,使 , 过点P作PQ垂直x轴,交双曲线于点Q,请直接写出线段PQ的长.

-
20、如图,在ABC中,是上的点, , , 分别是 , 的中点, , , 求 , 的长.
