相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、如图,已知 , 分别是等边三角形中 , 边上的点,且 , 连接 , , 交于点 . 请判断与之间有怎样的数量关系,并说明理由.

-
2、如图,A为和的公共顶点,已知 , , 请你添加一个条件,使得 . (不添加其他线条和字母)
 (1)、你添加的条件是________;(2)、根据你添加的条件,写出证明过程.
(1)、你添加的条件是________;(2)、根据你添加的条件,写出证明过程. -
3、如图,在平面直角坐标系中,的顶点 , , 均在正方形网格的格点上.
 (1)、画出将向右平移4个单位长度后得到的;(2)、画出关于轴对称的 , 并写出点的坐标.
(1)、画出将向右平移4个单位长度后得到的;(2)、画出关于轴对称的 , 并写出点的坐标. -
4、如图,直线是中边的垂直平分线,是直线上一动点.若 , , 则的周长的最小值是 .

-
5、如图,是等边三角形的中线,以点为圆心,的长为半径画弧,交边于点 , 连接 , 则的度数是 .

-
6、一个正多边形的每个内角等于 , 则它的边数是 .
-
7、如图,在长方形中, , 分别是 , 边上的点,连接 , 将长方形沿折叠,点落在点处,点落在点处,与边交于点 . 若四边形的周长是 , , 则四边形的周长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8、如图,在中, , , 分别以点A,为圆心,大于的长为半径作弧,两弧相交于 , 两点,作直线 , 交于点 , 连接 . 若 , 则的长为( )
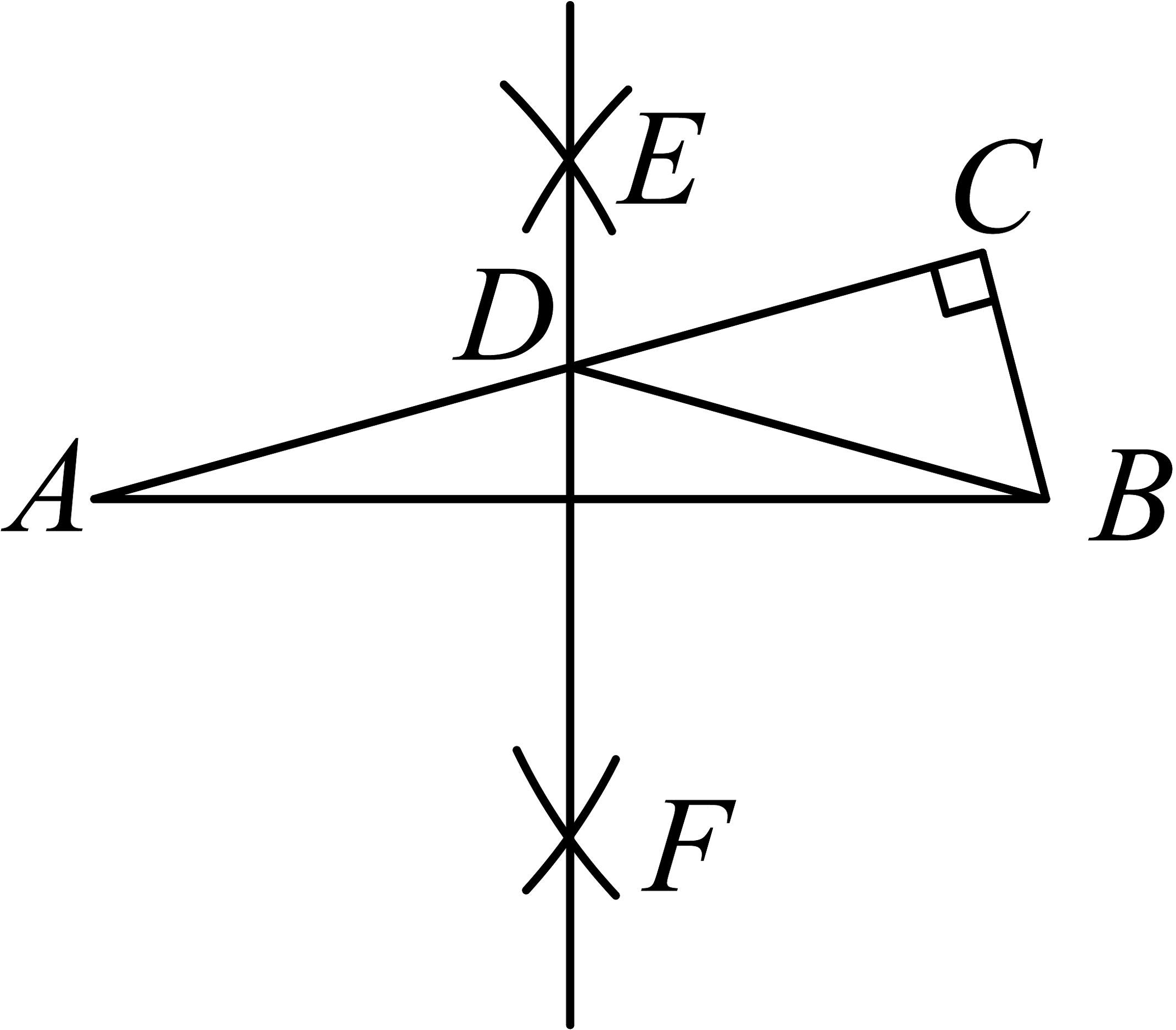 A、1 B、2 C、4 D、8
A、1 B、2 C、4 D、8 -
9、如图,在中, , , 平分 , 交于点 , 于点 , 且 , 则的周长是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10、给出下列说法:①三角形的三条高都在三角形的内部;②周长相等的两个三角形全等;③全等三角形的面积相等;④成轴对称的两个图形一定全等,全等的两个图形一定成轴对称.其中正确的有( )A、1个 B、2个 C、3个 D、4个
-
11、如图,在中, , , 分别是 , , 边上的中点,连接 , , . 已知的面积为4,则阴影部分的面积为( )
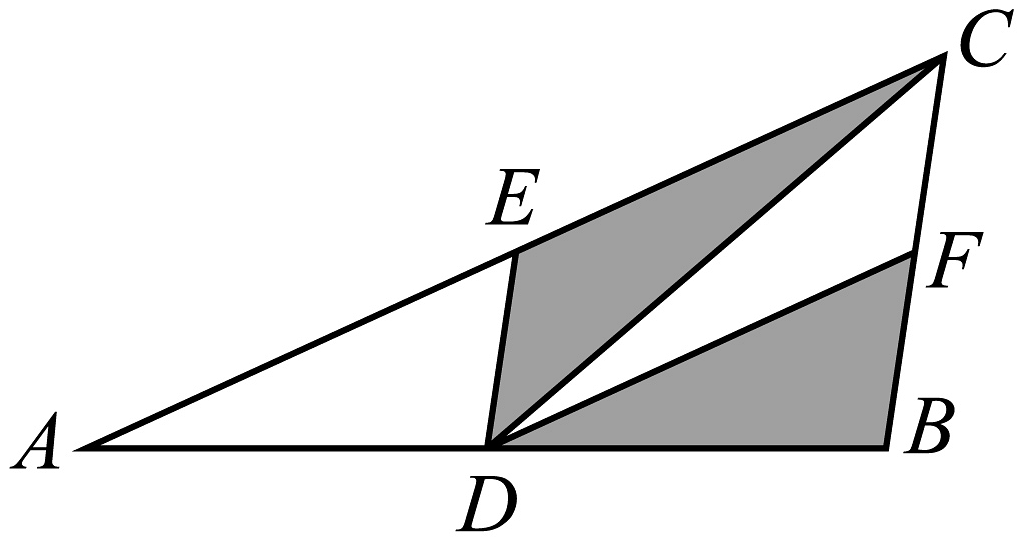 A、1 B、3 C、2 D、
A、1 B、3 C、2 D、 -
12、在平面直角坐标系中,已知点与点关于轴对称,则的值为( )A、 B、0 C、1 D、2024
-
13、如图,给长方形框架的展板增加两根支架和后,框架就能固定不倒,这样做的依据是( )
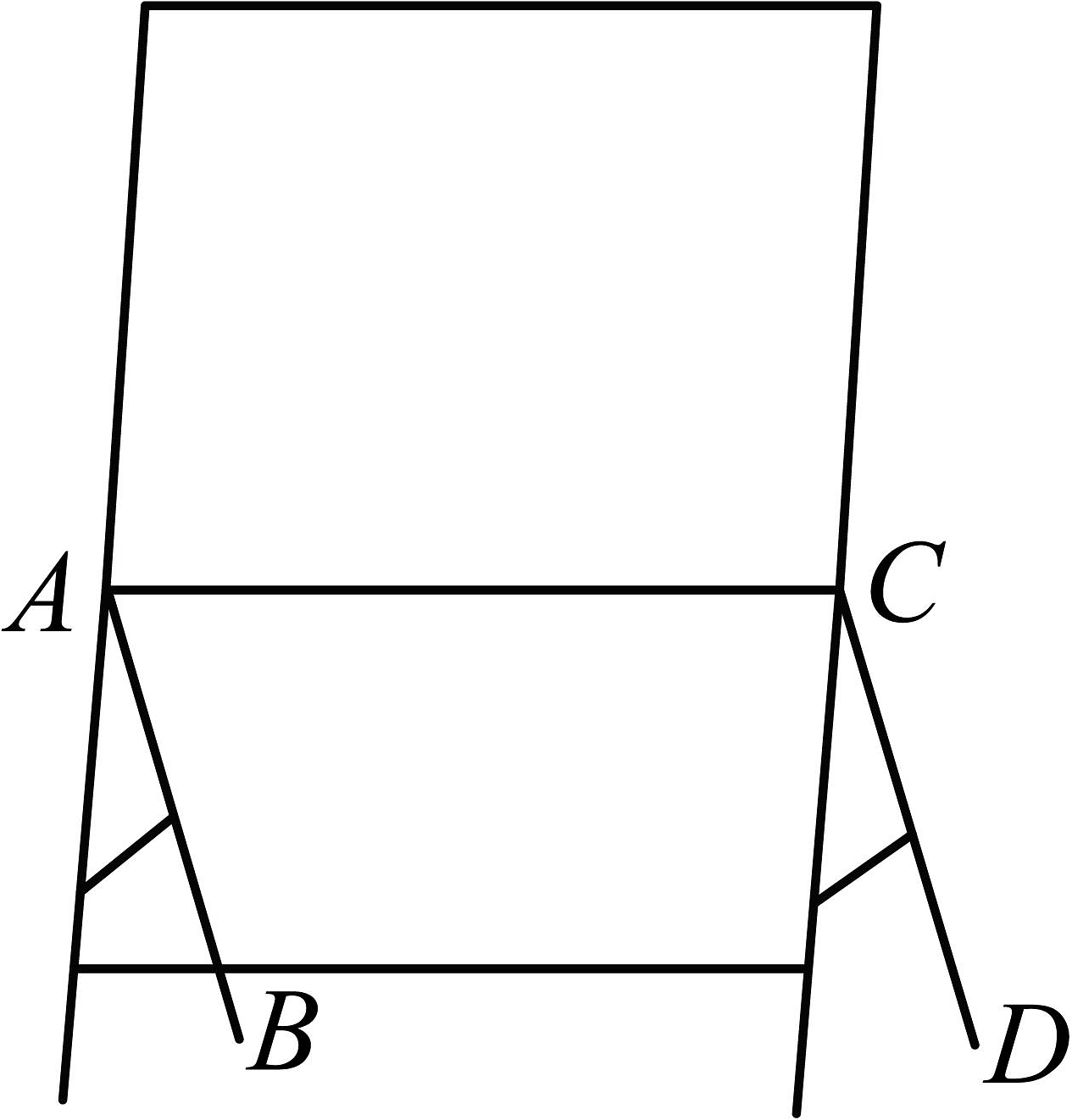 A、垂线段最短 B、两点之间,线段最短 C、两点确定一条直线 D、三角形具有稳定性
A、垂线段最短 B、两点之间,线段最短 C、两点确定一条直线 D、三角形具有稳定性 -
14、下列长度的各组线段中,能围成三角形的是( )A、3,7,10 B、10,5,7 C、3,10,5 D、4,4,10
-
15、近年来,中国新能源汽车产业蓬勃发展,呈现出强劲的增长势头,有着广阔的发展前景.众多数据表明,中国新能源汽车在国际市场上的竞争力不断增强.下面的国产新能源汽车的品牌标志中,不是轴对称图形的是( )A、
 B、
B、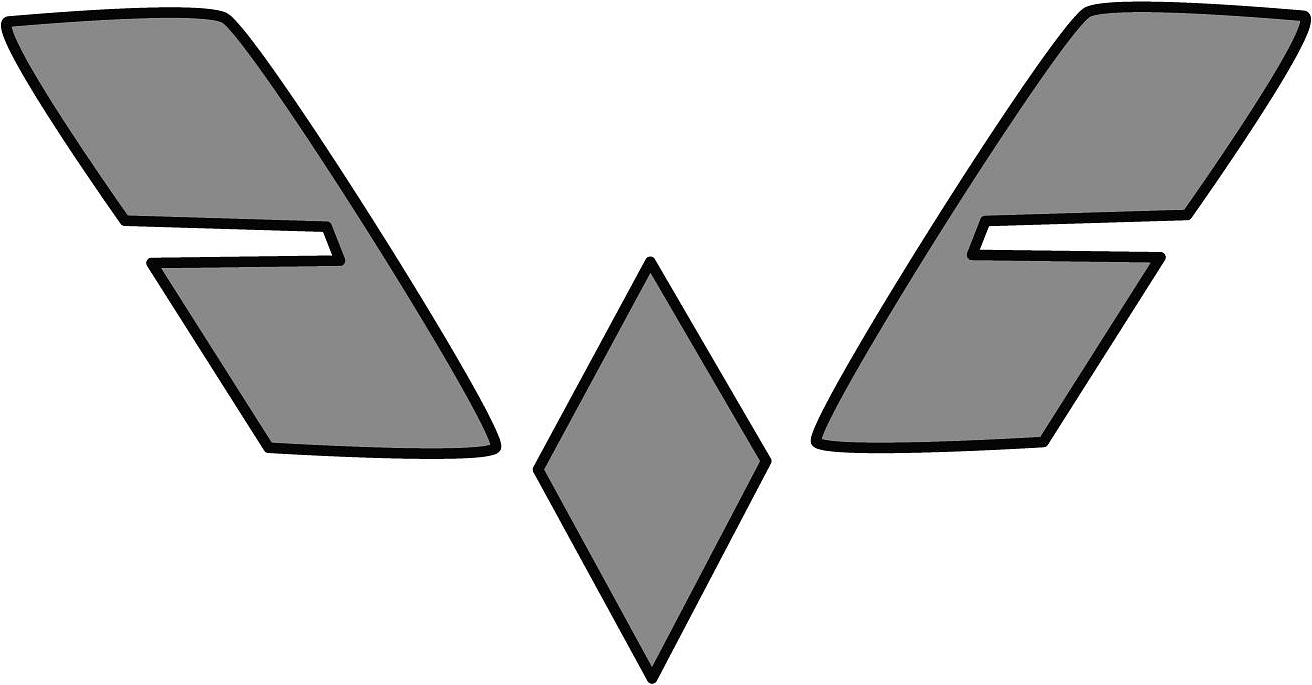 C、
C、 D、
D、
-
16、“赵爽弦图”是我国汉代的数学家赵爽创制的.以直角三角形的斜边为边得到一个正方形,该正方形由4 个全等的直角三角形再加上中间的小正方形组成.如图,在游园活动中,数学小组制作了一面“赵爽弦图锣”,其中∠ABC=90°,AC=50 cm,AB=30 cm,小明蒙上眼睛用棍子击中了锣面,他击中阴影部分的概率是.

-
17、 如图,转盘中黄色扇形的圆心角为120°,绿色扇形的圆心角为240°,现让转盘自由转动一次,则指针落在黄色区域的概率为.(注:当指针恰好指在分界线上时,无效重转)

-
18、 小滨和小江分别从甲、乙两个式样、大小都相同的不透明袋子中随机抽出一张卡片,其中,甲、乙两个袋子中均装有一张写着正数的卡片和一张写着负数的卡片.把各自抽出的卡片上的数字相乘,若乘积为正数则小滨获胜,若乘积为负数则小江获胜,则该 场 游 戏 小 江 获 胜 的 概 率 是.若在乙袋中增加一张写着负数的卡片,甲袋中的卡片数不变,两人按照上述规则再次游戏,则小江获胜的概率和第一场游戏中小江获胜的概率相比将.(填“增加”“减小”或“不变”)
-
19、 自《学校食品安全与营养健康管理规定》发布后,多地提出“校长陪餐制”,即校长陪学生吃午餐.如图是某校一张餐桌的示意图,学生甲先坐在D座位,校长和学生乙在A,B,C三个座位中随机选择两个座位,则校长和学生乙坐在正对面的概率是 ( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
20、在一个不透明的空袋子里,放入仅颜色不同的2个红球和1个白球.(1)、从中随机摸出1个球后不放回,再从中随机摸出1个球,两次都摸到红球的概率是;(2)、若从中随机摸出1个球后放回,再从中随机摸出1个球,两次都摸到红球的概率是;(3)、若一次性从中摸出两个球,则摸到两个红球的概率为.