相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、有一个数值转换器,原理如图所示,若开始输入x 的值是3,可发现第1次输出的结果是10,第2次输出的结果是5,第3次输出的结果是 , 依次继续下去…,第2 025 次输出的结果是.

-
2、已知a,b互为相反数,c,d互为倒数,m是绝对值最小的数,且求5a+ 的值.
-
3、已知a,b 互为相反数,c,d 互为倒数,|x-1|=2,求 的值.
-
4、已知a,b互为相反数,且a≠0,c,d 互为倒数,m 的绝对值等于3,求 的值.
-
5、中国“最美扶贫高铁”之一的“张吉怀高铁”开通后,张家界到怀化的运行时间由原来的3.5h缩短至 1 h,运行里程缩短了 40 km.已知高铁的平均速度比普通列车的平均速度每小时快200 km,求高铁的平均速度.
-
6、湿地公园具有湿地保护与利用、生态观光、休闲娱乐等多种功能.如图,某湿地公园有一块边长为100m的正方形湿地,为保证游客安全,通过编程使两只带有摄像功能的电子蚂蚁甲、乙沿着这个正方形湿地按A→B→C→D→A 的路线来回巡逻.蚂蚁甲从点A 出发,速度是 20 m/min,同时蚂蚁乙从点B 出发,速度是45 m/min,这两只电子蚂蚁第2 023次相遇时,是在这块正方形湿地的哪条边上?

-
7、甲车和乙车分别从 A,B两地同时出发相向而行,分别去往 B地和 A 地.两车匀速行驶2 h后相遇,相遇时甲车比乙车少走了20 km.相遇后,乙车按原速继续行驶1.8 h到达A地.(1)、求乙车的行驶速度.(2)、相遇后,甲车先以100 km/h的速度行驶了一段路程后,又以 120 km/h的速度继续行驶,刚好能和乙车同时到达目的地.试求相遇后,甲车以 100 km/h 的速度行驶的路程和以120 km/h的速度行驶的路程各是多少千米.
-
8、一队学生从学校出发去部队军训,以5k m/h的速度行进4.5k m时,一名通信员以14 km/h 的速度骑自行车从学校出发追赶队伍,他在离部队6 km处追上队伍,求学校到部队的路程.
-
9、一艘轮船航行在朝天门和钓鱼嘴两个码头之间,从朝天门到钓鱼嘴顺水航行用了3 h,逆水航行比顺水航行多用20 min,已知轮船在静水中的速度为19 km/h.(1)、求水流速度以及朝天门和钓鱼嘴两个码头之间的距离;(2)、若在这两地之间建立新的码头大坪湾,使该轮船从朝天门到大坪湾的航行时间是从钓鱼嘴到大坪湾航行时间的一半,问:朝天门和大坪湾两地相距多少千米?
-
10、一个机器人从数轴原点出发,沿数轴正方向以每前进3步后退2步的程序运动.设该机器人每秒前进或后退1步,并且每步的距离是1个单位长度,xn表示第ns时机器人在数轴上的位置所对应的数.有下列结论:①;②1;③;④.其中正确的结论是.(填序号)
-
11、如图,一电子跳蚤在数轴的点P0处,第一次向右跳1个单位长度到达点P1处,第二次向左跳2个单位长度到达点P2处,第三次向右跳3个单位长度到达点P3处,第四次向左跳4个单位长度到达点P4处……以此类推,当跳蚤第十次恰好跳到数轴原点时,点P。在数轴上表示的数为.

-
12、如图,数轴被折成90°,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字2所对应的点与数轴上的数字3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,则与数轴上的数2018重合的圆周上的数字是( )
 A、3 B、0 C、1 D、2
A、3 B、0 C、1 D、2 -
13、在数轴上点A表示的数是-5,点 M从点A 出发,先向左移动1个单位长度,再向右移动2个单位长度,再向左移动3个单位长度,再向右移动4个单位长度……依次操作4054次后,点M表示的数是( )A、2019 B、2 020 C、2 021 D、2 022
-
14、等边三角形ABC在数轴上的位置如图所示,点A,C对应的数分别为0和-1.若三角形ABC绕顶点沿顺时针方向在数轴上连续翻转,翻转1次后,点B对应的数为1,则连续翻转若干次后,数2024对应的点为.

-
15、已知a>0,b<0,且|a|<|b|,比较a,b,-a,-b的大小:.(用“<”连接)
-
16、若有理数a,b在数轴上的对应点的位置如图所示,则下列式子中正确的有.(填序号)

①b<0<a;②|b|<|a|;③ab>0;④a-b>a+b.
-
17、有理数a在数轴上的对应点的位置如图所示,有下列各数:①-a-1;②|a+1|;③2-|a|;④ |a|.其中在0到1之间的是( )
 A、①③④ B、②③④ C、①②③④ D、①②③
A、①③④ B、②③④ C、①②③④ D、①②③ -
18、在3,-|-3.5|,-(-3),0中,最小的数是( )A、3 B、-|-3.5| C、 D、0
-
19、有理数a,b,c在数轴上的对应点的位置如图所示.
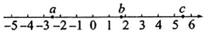 (1)、把下列各数在数轴上表示出来,并比较它们的大小,用“>”连接.
(1)、把下列各数在数轴上表示出来,并比较它们的大小,用“>”连接.-|-4|,2 , 0,-1.5,-(-5).
(2)、比较大小:①a0;②b0;③a+b0;④a+c0.(填>”或“<”)
-
20、若 求下列代数式的值:(1)、(2)、(3)、