相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、如图,在三角形纸片中, , , 将纸片沿着过点A的直线折叠,使点落在边上的点处,折痕交于点;再将纸片沿着过点的直线折叠,使点落在边上的点处,折痕交于点 . 下列结论成立的是( )
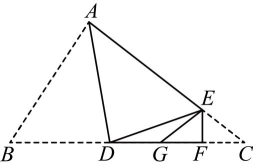 A、 B、 C、 D、
A、 B、 C、 D、 -
2、如图,四边形是的内接四边形, , , 直线与相切于点 . 若 , 则的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、下列计算正确的是( )A、 B、 C、 D、
-
4、如图,在平面直角坐标系中,点A , B , C都在格点上,将关于y轴的对称图形绕原点O旋转 , 得到 , 则点A的对应点的坐标是( )
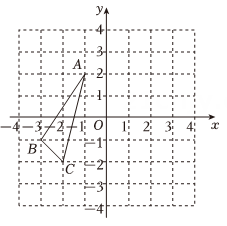 A、 B、 C、 D、
A、 B、 C、 D、 -
5、如图①,榫卯是古代中国建筑、家具及其它器械的主要结构方式.图②的左视图是( )
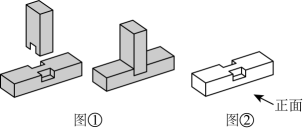 A、
A、 B、
B、 C、
C、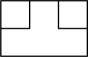 D、
D、
-
6、 2025年5月,我国在西昌卫星发射中心成功将行星探测工程天问二号探测器发射升空,天问二号探测器将对小行星2016HO3和主带彗星311P开启科学探测,其中一个目标所在轨道与太阳间距将达到亿公里.亿 , 将374000000用科学记数法表示为( )A、 B、 C、 D、
-
7、围棋是中华民族发明的博弈活动.下列用棋子摆放的图形中,既是轴对称图形,又是中心对称图形的是( )A、
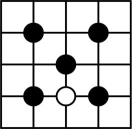 B、
B、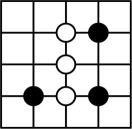 C、
C、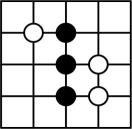 D、
D、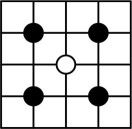
-
8、下列各式中,是不等式的是( )A、 B、 C、 D、
-
9、小茗同学发现一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形.小茗把具有这个规律的图形称为“手拉手”图形.如图所示的“手拉手”图形中,和均为等腰直角三角形, , , , 点在同一直线上,连接 , 为中边上的高.
 (1)、求证:;(2)、求的度数;(3)、直接写出和之间的数量关系.
(1)、求证:;(2)、求的度数;(3)、直接写出和之间的数量关系. -
10、先阅读下面例题的解法,再完成后面的问题.
例题:已知 , 求A,B的值.
解:将等式两边都乘得:
去括号整理得:
所以 , 解得
(1)、已知 , 求A,B的值;(2)、根据(1)中的结果,若 , 求x的值. -
11、如图,在中,的垂直平分线分别交 , 于点 , , 的垂直平分线分别交 , 于点 , .
 (1)、若 , 求的周长;(2)、若 , 求的度数.
(1)、若 , 求的周长;(2)、若 , 求的度数. -
12、先化简,再求值: , 其中 .
-
13、解下列分式方程:(1)、(2)、
-
14、计算;(1)、(2)、
-
15、已知 , , , , ……, , 根据规律,请计算(用含x的式子表示)
-
16、已知 , 则的值为 .
-
17、如图,在中,点D在上, , E为的中点,若 , 则 .

-
18、如图,在中, , , , 平分交于点 , 在上截取 , 则的周长为 .
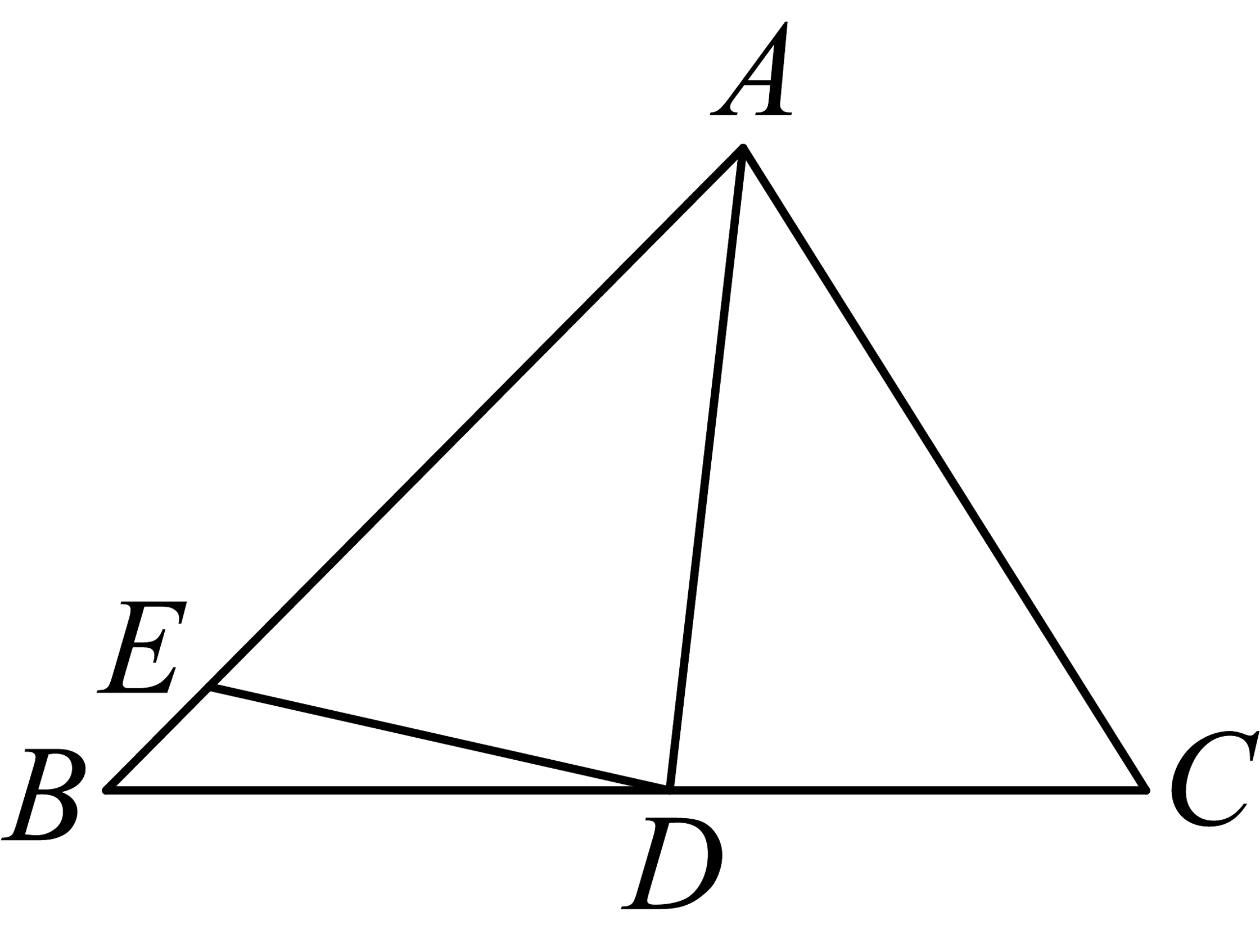
-
19、已知 , , 则的值为 .
-
20、计算: .