相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、在同一平面内,两条直线的位置关系可能是( )A、相交或垂直 B、平行或相交 C、垂直或平行 D、平行或相交或垂直
-
2、如图,直线、交于点O , 若 , 则的度数为( )
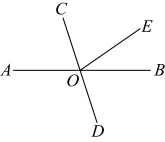 A、 B、 C、 D、
A、 B、 C、 D、 -
3、如图所示, , 为角的三等分线,过点C作关于的平行线交于点B , 则的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
4、如图,两直线 , 平行,则( )
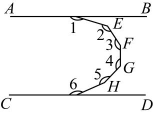 A、 B、 C、 D、
A、 B、 C、 D、 -
5、下列说法正确的有( )
①同位角相等:②对顶角相等;③过一点有且只有一条直线与已知直线平行;④在同一平面内,两条直线的位置关系有相交和平行两种.
A、1个 B、2个 C、3个 D、4个 -
6、如图,下列结论中错误的是( )
 A、与是同旁内角 B、与是内错角 C、与是内错角 D、与是同位角
A、与是同旁内角 B、与是内错角 C、与是内错角 D、与是同位角 -
7、下列选项中,和是对顶角的是( )A、
 B、
B、 C、
C、 D、
D、
-
8、数学活动

数形结合是数学学习的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题.
(1)、【知识生成】如图1是一个边长为的正方形,用两条分割线将其分为两个正方形和两个长方形,正方形的边长分别为a和b;图2是一个边长为a的正方形,用两条分割线将其分为两个正方形和两个长方形,正方形的边长分别为和b , 请分别写出阴影部分的面积所揭示的乘法公式:图1:;图2:;
(2)、【拓展探究】用4个全等的长和宽分别为a , b的长方形拼摆成一个如图3的正方形,请你直接写出阴影部分的面积所揭示的这三个代数式 , 之间的等量关系,并通过运算验证它的正确性.
(3)、【解决问题】如图4,长方形周长为 , , 求长方形的面积.
(4)、【知识迁移】若 , 则 . (直接写出结果)
-
9、关于的代数式化简后不含的项和常数项.(1)、分别求、的值;(2)、求的值.
-
10、分解因式(1)、;(2)、;(3)、;(4)、 .
-
11、先化简,再求值: , 其中和满足 .
-
12、化简求值:(1)、 , 其中, , ;(2)、已知 , 求代数式的值.
-
13、已知 , .(1)、求的值;(2)、求的值.
-
14、甲同学分解因式时看错了9,分解结果为 , 则多项式分解因式的正确结果为 .
-
15、若 , , 则 .
-
16、若的结果中不含项,则常数的值为 .
-
17、已知m、n为实数,且满足 , 则的算术平方根为 .
-
18、已知 , 则的值是( )A、6 B、7 C、8 D、10
-
19、已知 , , 则的值是( )A、8 B、9 C、6 D、7
-
20、已知 , , 则的值为( )A、10 B、9 C、8 D、7