相关试卷

1、已知二次函数 $y = - x^{2} + b x + c$ 的图象经过(-1，0)与(5，0)两点.若关于x 的方程 $- x^{2} + b x + c + d = 0$ 有两个根，其中一个根是6，则该方程的另一个根是.

查看解析
2、二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的部分图象如图所示，对称轴为直线x=1，与y轴的交点为(0，3)，与x轴的一个交点为(-1，0).

(1)、关于x 的方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的解为；

(2)、关于x 的方程 $a x^{2} + b x + c = 3 (a \neq 0)$ 的解为；

(3)、关于x的方程 $a x^{2} + b x + c = k (a \neq 0)$ 有两个不相等的实数根，则k 的取值范围为；

(4)、关于x的不等式 $a x^{2} + b x + c > 3 (a \neq 0)$ 的解为.

查看解析
3、在二次函数 $y = a x^{2} + b x - 2$ 中，x与 y 的几组对应值如下表：
x
··
—2
0
1

y

-2
-2
1

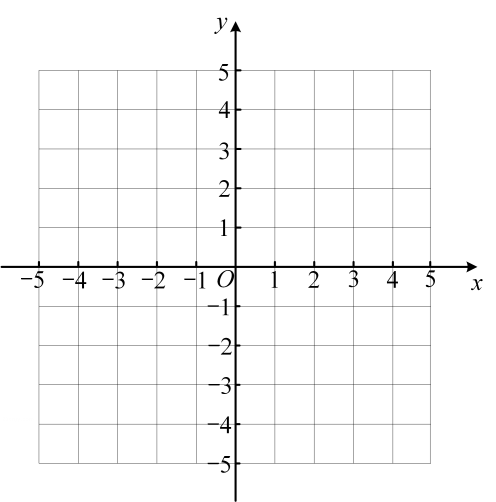(1)、求二次函数的表达式；

(2)、求二次函数图象的顶点坐标，并在给出的平面直角坐标系中画出二次函数的图象；

(3)、将二次函数的图象向右平移n个单位后，当0≤x≤3时，若图象对应的函数最大值与最小值的差为5，请直接写出n 的值.

查看解析
4、如图，在平面直角坐标系xOy中，二次函数 $y = a x^{2} - 4 x + 5 (a \neq 0)$ 的图象的顶点为 A，此图象与x轴交于点 B和点C，与y轴交于点 D.点A 的横坐标是-2.

(1)、求 B，C 两点的坐标；

(2)、平移该二次函数的图象，使点 A 恰好落在点D 的位置上，求平移后图象对应的二次函数的表达式.

查看解析
5、若将抛物线 $y = 2 x^{2} - 4 x + 5$ 向下平移m(m>0)个单位，向左平移n(n>0)个单位后得到的抛物线的表达式为y=2x² ，则m+n=

查看解析
6、如图，二次函数 $y = a x^{2} + b x + c (a ， b ，$ c 为常数，a≠0)的图象交x 轴于A，B 两点，点 A 的坐标是(-1，0)，点 B 的坐标是(n，0).有下列结论：①abc<0；②4a+c>2b；③关于x 的方程 $a x^{2} +$ bx+c=0的解是x₁=-1，x₂=n； $④ - \frac{b}{2 a} =$ $\frac{n - 1}{2} .$
其中正确的有( )

A、1个 B、2个 C、3个 D、4个

查看解析
7、关于 x 的二次函数 $y = m x^{2} - 2 m x + m + 1$ (m<-1)的图象可能是( )

A、 B、 C、 D、

查看解析
8、已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，则 ( )

A、abc<0 B、2a+b<0 C、2b-c<0 D、a-b+c<0

查看解析
9、已知二次函数 $y = - x^{2} + 2 a x - a + 3$ (a是常数).

(1)、若该函数图象的对称轴为直线x=1，求该函数的表达式；

(2)、当x≥a+1时，该函数的最大值为4，求a的值；

(3)、已知M(x₁ ， y₁)和 N(3a，y₂)是该函数图象上两点，当 $2 \leq x_{1} \leq 3$ 时，y₁

查看解析
10、已知二次函数 $y = a x^{2} - 4 a x + 3$ 的图象上有A(a，y₁)，B(4，y₂)两点，则下列说法正确的是( )

A、当0<a<2时， $y_{1} > y_{2}$ B、当a>2时， $y_{1} < y_{2}$ C、当a<0时， $y_{1} < y_{2}$ D、当a>4时， $y_{1} < y_{2}$

查看解析
11、已知二次函数y=x(x-a)+(x-a)(x-b)+x(x-b)，其中a，b为两个不相等的实数.

(1)、当a=0，b=3时，求此函数图象的对称轴.

(2)、当b=2a 时，若该函数在0≤x≤1时，y随x的增大而减小；在3≤x≤4时，y随x 的增大而增大，求a 的取值范围.

(3)、若点A(a，y₁)，B(a+b/₂ ， y₂)，C(b，y₃)均在该函数的图象上，是否存在常数m，使得 $y_{1} + m y_{2} + y_{3} = 0 ?$ 若存在，求出m 的值；若不存在，说明理由.

查看解析
12、已知抛物线 $y = a x^{2} + b x + 3 (a \neq 0)$ 的顶点坐标为(-2，-1)，下列说法正确的是( )

A、 $a = \frac{1}{2}$ B、当x=-2时，二次函数有最小值为3 C、当x>-2时，y随x 的增大而减小 D、当-3<x<-1时，y<0

查看解析
13、下表中y 与x 的数据满足我们初中学过的某种函数关系，求该函数的表达式.
x
··
-1
0
1
3

y

0
3
4
0

查看解析
14、已知一个二次函数的图象开口向下，顶点的坐标为(2，1)，那么这个二次函数的表达式可以是 .(只需写出一个即可)

查看解析
15、二次函数图象如图所示，则此函数的表达式为( )

A、 $y = x^{2} + 2 x - 3$ B、 $y = x^{2} - 2 x + 3$ C、 $y = x^{2} - 2 x - 3$ D、 $y = x^{2} + 2 x + 3$

查看解析

16、

表达式	适用情况
一般式：⑲	已知图象上三个点的坐标，特例：顶点在原点时：y=⑳ ；顶点在y轴上：y=㉑；顶点在x 轴上：y=a(x-h)²
顶点式：㉒	已知图象的顶点坐标，或者对称轴与最值
交点式：㉓	已知图象与x 轴的交点坐标(x₁ ， 0)，(x₂ ， 0)

查看解析

17、填空：

(1)、函数y=2(x+3)²的图象，可以由函数 $y = 2 x^{2}$ 的图象向平移个单位得到；

(2)、 $y = 2 x^{2}$ 的图象，可以由函数. $y = 2 {(x - 1)}^{2}$ 的图象向平移个单位得到；

(3)、函数 $y = 2 {(x - 1)}^{2}$ 的图象，可以由函数 $y = 2 {(x + 3)}^{2}$ 的图象向平移个单位得到.

查看解析

18、

平移前	平移m个单位 (m>0)	平移后	规律
$y = a x^{2}$ (a≠0)	向上平移m个单位	y=⑮	上“+”
	向下平移m个单位	y=⑯	下“一”
	向右平移m个单位	y=⑰	右“一”
	向左平移m 个单位	y=⑱	左“+”
【温馨提示】(1)任意抛物线 $y = a (x - h)^{2} + k (a \neq$ 0)均可由 $y = a x^{2}$ 平移得到，平移抛物线时a 不变； (2)抛物线的平移问题可转化为顶点的平移问题求解

查看解析

19、已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则下列说法正确的是( )

A、ac>0 B、a+b+c=0 C、4a+2b+c<0 D、2a+b=0

查看解析

20、

a>0⇔抛物线开口⑪ ；

a<0⇔抛物线开口向下；

|a|越大，抛物线开口越⑫

b，a

b=0⇔对称轴为 y轴；

ab>0(a，b同号)⇔对称轴在 y轴⑬ 侧；

ab<0(a，b异号)⇔对称轴在 y 轴⑭ 侧

c=0⇔抛物线过点(0，0)；

c>0⇔抛物线与y轴交于正半轴；

c<0⇔抛物线与y轴交于负半轴

查看解析

上一页 508 509 510 511 512 下一页跳转

x	··	—2	0	1
y		-2	-2	1

x	··	-1	0	1	3
y		0	3	4	0