相关试卷
- 2017-2018学年北师大版数学八年级下册同步训练:6.4 多边形的内角和与外角和
- 2017-2018学年北师大版数学八年级下册同步训练:6.3 三角形的中位线
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.2 平行四边形的判定 ——用对角线的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.1 平行四边形的判定——用边的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.4分式方程课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.4 分式方程课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时1
-
1、嘉淇同学用配方法推导一元二次方程ax2+bx+c=0(a≠0)的求根公式时,对于b2-4ac>0的情况,她是这样做的:
由于 , 方程变形为:
, .............................第一步
, ............第二步
, ...................第三步
, ...........第四步
............................第五步
(1)、嘉淇的解法从第步开始出现错误;事实上,当b2-4ac>0时,方程ax2+bx+c=0(a≠0)的求根公式是.(2)、用配方法解方程:x2-2x-24=0. -
2、如图,正方形ABCD的边长为2,点B与原点O重合,与反比例函数的图象交于E、F两点,若的面积为 , 则k的值

-
3、如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2,点D是AB边上的中点,以点D为圆心,BD的长为半径作弧BC.则图中阴影部分的面积为.
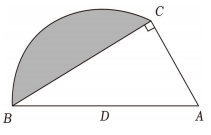
-
4、如图,等边三角形ABC是由9个大小相等的等边三角形构成,随机地往△ABC内投一粒米,这粒米落在阴影区域的概率为.
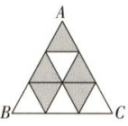
-
5、如图1,E为矩形ABCD边AD上一点,点P从点C沿折线CD-DE-EB运动到点B时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )
 A、 B、当时,是等腰三角形 C、当时, D、
A、 B、当时,是等腰三角形 C、当时, D、 -
6、某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点,当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF//BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
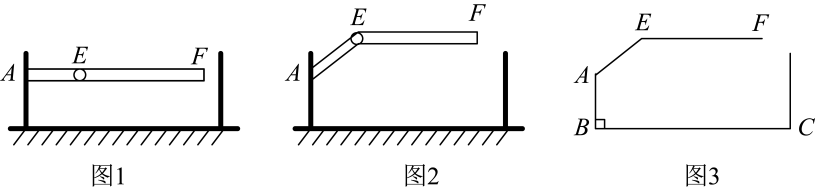 A、
A、 B、
B、 C、
C、 D、
D、
-
7、如图,在矩形ABCD中,AD>AB,AB=5cm,AC,BD交于点O,∠AOD=2∠AOB=120°,则BC=( )
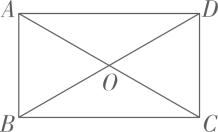 A、5cm B、cm C、cm D、cm
A、5cm B、cm C、cm D、cm -
8、如图,在△ABC中AD平分∠BAC,按以下步骤作图:第一步分别以点A、D为圆心,以大于AD的长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别AB、AC于点E、F;第三步,连接DE、DF,若BD=6,CD=3,CF=2,则AE的长是( )
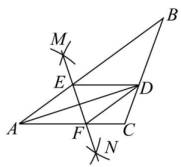 A、4 B、4.5 C、5 D、5.5
A、4 B、4.5 C、5 D、5.5 -
9、如图,已知 , , 点B、O、D在同一条直线上,则的度数为( )
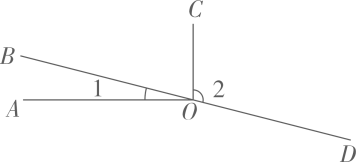 A、102° B、118° C、122° D、62°
A、102° B、118° C、122° D、62° -
10、在对一组样本数据进行分析时,小华列出了方差的计算公式: , 由公式的提供信息,则下列说法正确的是( )A、样本的平均数是3.5 B、样本的众数是3 C、样本的中位数是3 D、样本的容量是4
-
11、下列运算正确的是( )A、 B、 C、 D、
-
12、在 , 0,5中,负数的个数有( )A、4个 B、3个 C、2个 D、1个
-
13、 如图,AB为⊙O的直径,弦CD⊥AB于点F,直径DE交弦CB于点H,弦AE分别交CD,CB于点M,G,连结OG.
 (1)、①写出图中所有与相等的弧 .
(1)、①写出图中所有与相等的弧 .②求证:OG⊥AB.
(2)、若GC2 =GH·GB,求∠B的度数.(3)、当GC=HB时,AB=6,求CD的长. -
14、 如图,已知抛物线y=-x2-2ax+5与x轴交于点A,C(点A在点C的右边),与y轴交于点B,OB=5OC.
 (1)、求抛物线的解析式及顶点坐标;(2)、当-1≤x≤7时,求二次函数y=-x2-2ax+5的最大值与最小值的差;(3)、点P为抛物线上任意一点,将点P向下平移2个单位长度得到点P1 , 若点P1关于原点O的对称点P2恰好落在抛物线上,求此时点P的坐标.
(1)、求抛物线的解析式及顶点坐标;(2)、当-1≤x≤7时,求二次函数y=-x2-2ax+5的最大值与最小值的差;(3)、点P为抛物线上任意一点,将点P向下平移2个单位长度得到点P1 , 若点P1关于原点O的对称点P2恰好落在抛物线上,求此时点P的坐标. -
15、小度同学步行从A地前往B地,小艺同学骑自行车沿同一条路从B地前往A地,两人同时出发,行进过程中速度均保持不变,如图所示反映了小度、小艺两位同学距离B地的路程y(m)与小度同学所用的时间x(min)之间的函数关系,请结合图像回答下列问题.
 (1)、小度同学步行速度为m/ min;(2)、小艺同学途中休息时间为min;(3)、当小艺同学到达A地时,求小度同学距离B地的路程;(4)、求出发多少时间小度、小艺两人途中相遇,
(1)、小度同学步行速度为m/ min;(2)、小艺同学途中休息时间为min;(3)、当小艺同学到达A地时,求小度同学距离B地的路程;(4)、求出发多少时间小度、小艺两人途中相遇, -
16、如图,在平行四边形ABCD中,点E、F分别在边AD、BC上,且AE=CF,连结EF,请仅用无刻度的直尺画出线段EF的中点O,并说明这样画的理由,

-
17、某农机公司为更好地服务于麦收工作,按图1给出的比例,从甲、乙、丙三个工厂共购买了150台同种农机,公司技术人员对购买的这批农机全部进行了检验,绘制了如图2所示优等品台数的统计图,

请你根据图中提供的信息,解答以下问题:
(1)、求该农机公司从丙厂购买农机的台数;(2)、求该农机公司购买的150台农机中优等品的台数;(3)、如果购买的这批产品质量能代表各厂的产品质量状况,那么:①从优等品占比的角度考虑,哪个工厂的产品质量较好?为什么?
②估计甲厂生产的360台产品中的优等品有多少台?
-
18、 如图,已知在锐角三角形ABC中, , ,
 (1)、 求BD的长.(2)、求cosC的值.
(1)、 求BD的长.(2)、求cosC的值. -
19、 解方程组:
-
20、 计算:.