相关试卷

1、“儿童散学归来早，忙趁东风放纸鸢”，风筝古称纸鸢，起源于春秋战国时期，风筝制作技艺已被列人国家非物质文化进产名录，为丰富校园生活，某校开展风筝制作活动，小言和哥哥制作了一大一小两个形状相同的风筝，风筝的形状如图所示，其中对角线AC⊥BD。已知大、小风筝的对应边之比为3：1，如果小风筝两条对角线的长分别为30cm和35cm，那么大风筝两条对角线长的和为cm.

查看解析
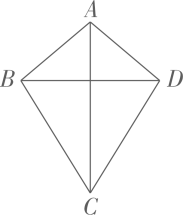
2、如图，把平行四边形纸片ABCD沿对角线AC折叠，点B落在点B'处.B'C与AD相交于点E，此时△CDE恰为等边三角形，若AB=6cm，则AD=cm

查看解析
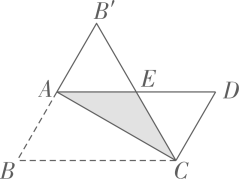
3、已知点A（2，y₁）.B（6，y₂）在反比例函数y= $\frac{k}{x}$ （k≠0）的图象上，如果y₁＞y₂那么k=（请写出一个符合条件的k值）

查看解析
4、方程 $\frac{2 x}{x - 1} = 1$ 的解是.

查看解析
5、如图1，在等腰直角三角形ABC中，∠ACB=90°，点D为边AB的中点.动点P从点A出发，沿边AC→CB方向匀速运动，运动到点B时停止.设点P的运动路程为x，△APD的面积为y，y与×的函数图象如图2所示，当点P运动到CB的中点时，PD的长为（）

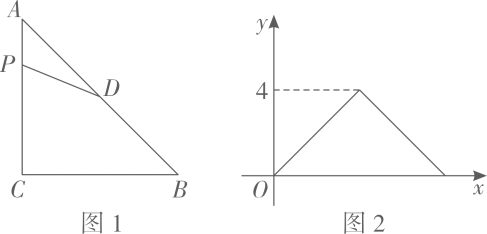A、2 B、2.5 C、 $2 \sqrt{2}$ D、4

查看解析
6、如图，一个圆形喷水池的中央竖直安装了一个柱形喷水装置OM，喷头M向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，按如图所示的直角坐标系，水流喷出的高度y（m）与水平距离x（m）之间的关系式是 $y = - x^{2} + 2 x + \frac{7}{4} (x > 0)$ ，则水流喷出的最大高度是（）

A、3m B、2.75m C、2m D、1.75m

查看解析
7、习近平总书记致首届全民阅读大会举办的贺词增出：阅读是人类获取知识，启智增惠、培养遐想的重要途径，可以让人得到思想启发，树立崇高理想，养浩然之气。中华民族自
古提倡阅读，讲究格物致知、诚意正心，传承中华民族生生不息的精神，塑造中国人民自信自强的品格。如图是某网站连续多年对其用户书籍阅读量的统计图，下列结论错误的是（）

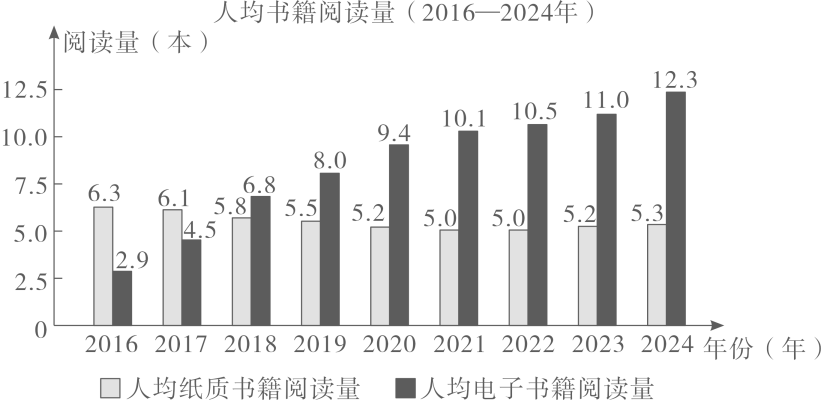A、2022年，人均纸质书阅读量为5本 B、2023年，人均电子书籍阅读量为11本 C、2024年，人均电子书籍阅读量是人均纸质书籍阅读量的3倍 D、2016年至2024年，人均电子书箱阅读量逐年上升

查看解析
8、如图，四边形ABCD内接于⊙O， $\overset{⌢}{A B} = \overset{⌢}{B C}$ ，连接BD，若∠ABC=70°，则∠BDC的度数为（）

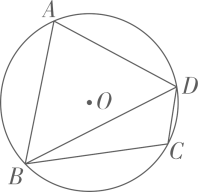A、20° B、35° C、55° D、70°

查看解析
9、如图，一个多边形纸片的内角和为1620°，按图示的剪法剪去一个内角后，所得新多边形的边数为（）

A、12 B、11 C、10 D、9

查看解析
10、关于x的一元二次方程3x²-6x+m=0有两个实数根，则m的取值范围是（）

A、m<3 B、m≤3 C、m>3 D、m≥3

查看解析
11、如图1，三根木条a，b，c相交成∠1=80°，∠2=110°，固定木条b，c，将木条a绕点A顺时针转动至如图2所示，使木条α与木条b平行，则可将木条旋转（）

A、30° B、40° C、60° D、80°

查看解析
12、根据国家统计局的数据，2024年中国生产芯片约45142000000颗，彰显了中国芯片业的强大实力.数据45142000000用科学记数法可以表示为（）

A、 $4.5142 \times 1 0^{9}$ B、 $4.5142 \times 1 0^{10}$ C、 $4.5142 \times 1 0^{11}$ D、 $4.5142 \times 1 0^{12}$

查看解析
13、如图，点D是Rt△ABC斜边AB上的一点，以BD为直径的圆⊙O交边AC于E，F两点，连结DE，BE，BF，并且BE平分∠DBF，

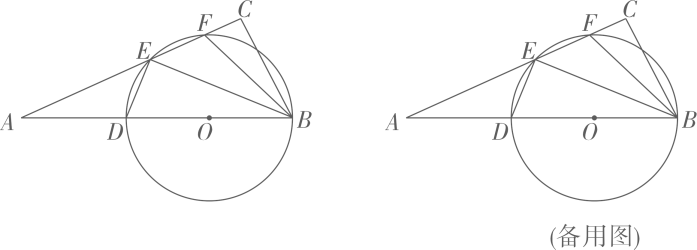(1)、求证： △BCF∽△BED ；

(2)、若DE=2.5，CF=2，求BC的长；

(3)、若BD=2AD，BF =8，求CF的长.

查看解析
14、在平面直角坐标系中，二次函数的表达式为 $y = m x^{2} + (m + 1) x + n$ ，其中 $m - n = 4$ .

(1)、若此函数图象过点（2， 5），求这个二次函数的表达式；

(2)、若 $(x_{1}, y_{1})$ ， $(x_{2}, y_{2})$ 为此二次函数图象上不同的两个点，当 $x_{1} = 4 - x_{2}$ 时， $y_{1} = y_{2}$ ，求 m 的值；

(3)、若点（-1， t）在此二次函数图象上，当 $x \geq - 1$ 时，y 随 x 的增大而增大，求 t 的取值范围.

查看解析

15、综合与实践：

背景：当前排球渐渐走入初中生的学习和生活中，排球运动不仅能提升身体素质，还

能促进心理健康，对青少年的身心发展有着诸多益处。

排球的购买与售卖

素材1：为了能让学生日常锻炼“排球垫球”体育运动，某中学打算购进一批排球，计划购买甲品牌的排球35个，乙品牌的排球50个，共花费3550元，已知购买一个甲品牌的排球比购买一个乙品牌的排球少花20元.

素材2：某商店售卖丙品牌排球，进价为每个20元，当前售价为每个36元，每周可售出50个，经市场调查发现，售价每降低3元，每周可多售出15个.

任务1：求购买一个甲品牌、一个乙品牌的排球各需多少元？

任务2：求当一个丙品牌的排球售价为多少元时有最大利润？最大利润是多少？

查看解析

16、某校组织九年级学生参加研学活动，为了确定本次研学的目的地，学校对学生去向意愿进行了摸底调查（A：农家乐；B：科技馆；C：大学城）.下面两幅统计图反映了抽取的部分学生对研学活动去向意愿的情况，请你根据图中的信息回答下列问题：

(1)、本次调查抽取的学生总人数为 ▲ 人，并补全条形统计图；

(2)、求扇形统计图中选项B所对应的圆心角度数；

(3)、若该校九年级的总人数为250人，试估计选择去大学城研学的总人数

查看解析
17、观察下面的等式：
第 1 个等式： $\frac{1}{1 \times 3} = \frac{1}{2} \times (1 - \frac{1}{3})$ ，
第 2 个等式： $\frac{1}{2 \times 4} = \frac{1}{2} \times (\frac{1}{2} - \frac{1}{4})$ ，
第 3 个等式： $\frac{1}{3 \times 5} = \frac{1}{2} \times (\frac{1}{3} - \frac{1}{5})$ ，
第 4 个等式： $\frac{1}{4 \times 6} = \frac{1}{2} \times (\frac{1}{4} - \frac{1}{6})$ ，
……
按照以上规律，解决下列问题：

(1)、写出第 5 个等式：；

(2)、请你猜想第 n 个等式（用含 n 的式子表示），并证明.

查看解析
18、如图，平行四边形ABCD中，AE平分∠BAD交BC于点E.

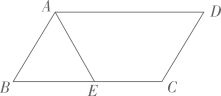(1)、尺规作图：作CF平分∠BCD交AD于点F（不写作法，保留作图痕迹）；

(2)、求证：四边形AECF是平行四边形.

查看解析

19、佳佳计算分式方程

\frac{1 - x}{x - 3} = \frac{1}{3 - x} - 2

的过程如下：

解方程： $\frac{1 - x}{x - 3} = \frac{1}{3 - x} - 2$

去分母，得 $1 - x = - 1 - 2$ 第①步

移项，得 $- x = - 1 - 2 + 1$ 第②步

合并同类项，得 $- x = - 2$ 第③步

系数化1，得 $x = 2$ 第④步

经检验， $x = 2$ 是该分式方程的解.

(1)、佳佳在计算过程中，第一次出现错误的步骤是（填序号）；

(2)、请你写出正确的解答过程.

查看解析

20、

(1)、计算： $s i n 3 0^{°} + | - \frac{3}{2} | - \sqrt{9}$ ；

(2)、解方程： $x^{2} + 2 x = 8$ .

查看解析

上一页 827 828 829 830 831 下一页跳转