相关试卷
- 2017-2018学年北师大版数学八年级下册同步训练:6.4 多边形的内角和与外角和
- 2017-2018学年北师大版数学八年级下册同步训练:6.3 三角形的中位线
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.2 平行四边形的判定 ——用对角线的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.1 平行四边形的判定——用边的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.4分式方程课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.4 分式方程课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时1
-
1、如图,台球运动中母球击中桌边上的点 , 经桌边反弹后击中相邻桌边上的点 , 再次反弹后击中球提示: ,
 (1)、若 , 求的度数;(2)、已知 , 母球经过的路线与一定平行吗?请说明理由.
(1)、若 , 求的度数;(2)、已知 , 母球经过的路线与一定平行吗?请说明理由. -
2、已知 , .(1)、求的值;(2)、求的值;(3)、设为常数且 , 若 , 求的值.
-
3、某班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后郗进行了测试.现将项目选择情况及训练前后篮球定时定点投测试成绩整理作出如下统计图表.

训练后篮球定时定点投篮测试进球数统计表:
进球数个
人数
请你根据图表中的信息回答下列问题
(1)、送择长跑训练的人数占全班人数的百分比是 , 该班共有同学人;(2)、直接补全“训练前篮球定时定点投测试进球数统计图”;(3)、若全区共有该年级学生人,请估计参加训练后篮球定时定点投篮进球数达到个以上包含个多少人? -
4、解方程组:(1)、;(2)、 .
-
5、计算:(1)、;(2)、 .
-
6、已知甲、乙两个长方形,它们的边长如图为正整数 , 甲、乙的面积分别为 , .
 (1)、与的大小关系为:;用“”、“”、“”填空(2)、若满足条件的整数有且只有个,则的值为 .
(1)、与的大小关系为:;用“”、“”、“”填空(2)、若满足条件的整数有且只有个,则的值为 . -
7、关于 , 的方程组的解满足 , 则的值为 .
-
8、如图,直线 , 将直角三角板按如图方式放置,直角顶点在上,若 , 则 .

-
9、某班进行体育中考模拟测试,按测试成绩将人分成个小组,第组的频率是 , 则第小组有名同学.
-
10、折纸不仅具有艺术审美价值,还蕴含着许多数学知识如图,一张长方形纸片 , 点 , 分别是线段 , 上的点,先将纸片沿折叠,点 , 的对应点分别为点 , , 与线段交于点 , 点是线段上一点,再将纸片沿折叠,点的对应点为点 , 点恰好在上,若测得 , 则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、如图所示,下列推理不正确的是( )
 A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 , -
12、根据下列运算结果,实数 , , , 中最大的是( )A、 B、 C、 D、
-
13、《算法统宗》中有这样一个问题如图 , 其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两请问:所分的银子共有多少两?注:明代时斤两,故有“半斤八两”这个成语设有个人,两银子,根据题意可以列方程组为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、下列调查适合做抽样调查的是( )A、对搭乘高铁的乘客进行安全检查 B、审核书稿中的错别字 C、调查一批节能灯管的使用寿命 D、对七班同学的视力情况进行调查
-
15、分式有意义的条件是( )A、 B、 C、 D、
-
16、计算的结果是( )A、 B、 C、 D、
-
17、如图,四边形为圆的内接四边形,连结和 , 在的延长线上取一点 , 连结 , 延长交于点 .
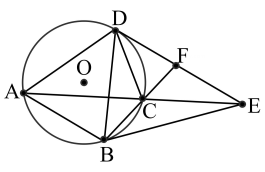 (1)、若为的中点, , 求的度数.(2)、当时,
(1)、若为的中点, , 求的度数.(2)、当时,①求证: .
②若点为的中点,求证: .
-
18、如图,二次函数的图象与轴交于两点,与轴交于点 .
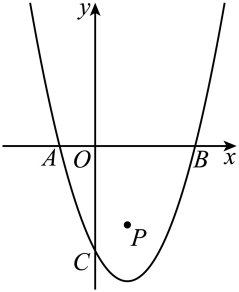 (1)、求二次函数解析式和顶点坐标.(2)、坐标平面内存在点P,满足向左、向右或向下平移个单位后均落在二次函数图象上,求平移的距离 .(3)、在二次函数图象上取点(不与点重合),使得在之间的图象上(含两点),该二次函数最大值与最小值的和等于1,请直接写出点的坐标.
(1)、求二次函数解析式和顶点坐标.(2)、坐标平面内存在点P,满足向左、向右或向下平移个单位后均落在二次函数图象上,求平移的距离 .(3)、在二次函数图象上取点(不与点重合),使得在之间的图象上(含两点),该二次函数最大值与最小值的和等于1,请直接写出点的坐标. -
19、小明和小白两人从同一地方出发,分别自驾前往外的景点游玩,小明与小白在服务区均休息了一次,每人每次休息30分钟.行驶过程中,两人的速度始终保持不变,具体时间与路程信息如图所示.
 (1)、求两人的行驶速度.(2)、求小白休息后的(段)行驶路程关于时间x的函数.(3)、求小明追上小白时的时间a.
(1)、求两人的行驶速度.(2)、求小白休息后的(段)行驶路程关于时间x的函数.(3)、求小明追上小白时的时间a. -
20、如图,在中, , 利用尺规以点为圆心,线段的长为半径作弧,交于点 , 分别以点为圆心,大于的长为半径作弧,两弧交于点 , 作射线 , 交边于点 .
 (1)、求证: .(2)、求的长.
(1)、求证: .(2)、求的长.