相关试卷

1、如图，点A，B，C，D为正n边形的顶点，点O为正n边形的中心，若∠ADB=20°，则n= ( )

A、七. B、八. C、九. D、十.

查看解析
2、若二次函数 $y = a x^{2} + b x + c (a b < 0, c > 0),$ 则这个函数图象可能是( )

A、 B、 C、 D、

查看解析
3、如图，弦AB， CD都是⊙O的直径，若∠AOC=28°，则∠C= ( )

A、10°. B、14°. C、18°. D、28°.

查看解析
4、抛物线. $y = {(x + 2)}^{2} - 3$ 的顶点坐标是( )

A、(2， 3). B、(-2， 3). C、(-2， - 3). D、(2， - 3).

查看解析
5、已知⊙O 的半径是5，点P在圆外，则线段OP 的长可能是( )

A、2. B、4. C、5. D、7.

查看解析
6、根据以下素材，完成设计货船通过双曲线桥的方案：一座曲线桥如图1所示，当水面宽AB=16米时，桥洞顶部离水面距离CD =4米.已知桥洞形如双曲线，图2是其示意图，且该桥关于CD对称.如图4，一艘货船露出水面部分的横截面为矩形EFGH，测得EH =8米.因水深足够，货船可以根据需要运载货物.据调查，船身下降的高度h(米)与货船增加的载重量t(吨)满足函数表达式 $h = \frac{1}{10} t .$

(1)、确定桥洞的形状.建立平面直角坐标系如图3所示，CD落在第一象限的角平分线上.设点C为(m，m)，
①点A 的坐标.(用m的代数式表示)；
② 求出经过点A 的双曲线的函数表达式.

(2)、这艘货船运载货物高3米(即EF=3米)，此时货船能通过该桥洞吗?若能，请说明理由；若不能，至少要增加多少吨货物?(已知 $\sqrt{10} \approx 3.2, \sqrt{13} \approx 3.6 .)$

查看解析
7、如图1，在△ABC中， AB =AC，点D、E分别在边AB、AC上，AD =AE，连接DC，点F、P、G分别为DE、DC、BC的中点，连接FP， PG.

(1)、图1中，求证： PF = PG；

(2)、当△ADE绕点A旋转到如图2所示的位置时，
①PF =PG是否仍然成立?若成立请证明；若不成立，说明理由；
② 若AD：AB =1：n(n>1)， △PDF和△PGC的面积分别是S₁ ， S₂ ， △ABC的面积为S₃ ，求 $\frac{S_{1} + S_{2}}{S_{3}}$ 的值.

查看解析
8、如图， A， B， C， D在⊙O上， AB∥CD，经过圆心O的线段EF⊥AB于点 F，与CD交于点 E.

(1)、如图1，当⊙O半径为5， $C D = 4 \sqrt{6}$ ，若EF=BF，求弦AB的长；

(2)、如图2，当⊙O半径为 $\sqrt{30}, C D = 2 \sqrt{6},$ 若OB⊥OC，求弦AC的长.

查看解析
9、如图，正方形ABCD中， E， F分别为边AD， CD上的点，且∠EBF =45°，求线段AE， CF， EF之间的数量关系.在小组学习过程中，我们得到了如下的解决方法：延长DA到G，使得AG =CF，再连接BG，利用△BEF≌△BEG可得EF = EG，即EF = AE+CF拓展延伸：

(1)、如图①，正方形ABCD中， E， F分别为边AD， CD上的点，且∠EBF =45°，已知AE=2， DF =3. 试求正方形ABCD的周长.

(2)、如图②，在正△ABC外作一等腰△ADC， DA=DC， ∠ADC=120°，以D为顶点作一个60°角，角的两边分别交AB， BC于E， F两点，连结EF.
① 求线段AE，CF，EF之间的数量关系，并加以证明；
② 已知△BEF的周长为12， △DEF的面积为4 $\sqrt{3}$ ，试求EF的长.

查看解析
10、已知抛物线 $y = - \frac{1}{2} x^{2} + b x + c$ ：经过点(1，0)，(0， $\frac{3}{2}$ )

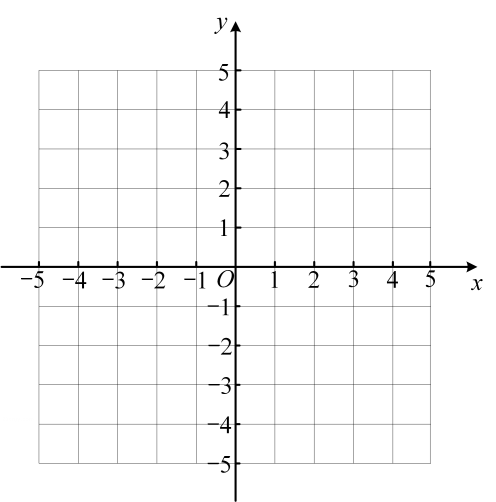(1)、求该抛物线的函数表达式；

(2)、求出抛物线与坐标轴的交点，并在如图坐标系中用描点法描出二次函数的图象.

查看解析
11、如图，在△ABC中， D是AB边上一点， G是AC边上一点，过点G作GF∥CD交AB于点 F， E是BC边上一点，连接DE， ∠1+∠2 = 180°.

(1)、判断AC与DE是否平行，并说明理由.

(2)、若DE平分∠BDC， ∠B =80°， ∠DEC =3∠A+20°，求∠ACD的度数

查看解析
12、如图，△ABC是边长为10cm的等边三角形.动点P和动点Q分别从点B和点C同时出发，沿着△ABC逆时针运动，已知动点P的速度为1cm/s，动点Q的速度为2cm/s.设动点P、动点Q的运动时间为 ts.

(1)、当t为何值时，两个动点第一次相遇；

(2)、从出发到第一次相遇这一过程中，当t为何值时，以P，Q，C为顶点的三角形的面积为 $8 \sqrt{3} c m ?$

查看解析
13、如图，AB为⊙O的直径，P是⊙O上一点，以P为圆心，适当长为半径作弧交直径AB所在的直线于点C，D；分别以 C，D为圆心，大于 $\frac{1}{2}$ CD长为半径作弧两弧交于点E；连结PE并延长交⊙O于点F，交AB于点G；以B为圆心，PF长为半径作弧交⊙O于点M，连结AM，若AM=10， BG=1，则⊙O的半径长是.

查看解析
14、将 $\sqrt{1} 、 \sqrt{2} 、 \sqrt{3} 、 \sqrt{4}$ .按如图方式排列.若规定(x，y)表示
第x排从左向右第y个数，则：
①(7，6)表示的数是；
在(x，y)，则x+y的值为.

查看解析
15、已知方程： $x^{4} - 3 x^{3} + 4 x - 1 = 0$ 有4个根x₁ ， x₂ ， x₃ ， x₄. 则( $(x_{1}^{2} - 1) (x_{2}^{2} - 1) (x_{3}^{2} - 1) (x_{4}^{2} - 1) =$ .

查看解析
16、如图，下边横排中有无数个方格，每个方格中都有一个数字，且任意相邻三个格子中数字之和都相等.已知，第1个方格中的数字是5，第9个方格中的数字是-6，前101个方格中的数字之和是74，则第101个方格中的数字是.
5
-6

查看解析
17、如图， AB∥DC， M和N分别是AD和BC的中点，连结CM， DN并延长，分别交AB于Q， P，若四边形ABCD的面积为24cm² ，那么 $S_{△ Q P O} - S_{△ C D O} =$ cm².

查看解析
18、如图，该款载物机器狗的最快移动速度v(m/s)与载重后总质量M (kg)成反比例，已知该款机器狗载重后总质量M为50kg时，它的最快移动速度v为7m/s；若其最快移动速度v大于 14m/s，则其载重后总质量M的取值范围是kg.

查看解析
19、如图，过原点的直线与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象交于A，B两点，点A在第一象限.点C在x轴正半轴上，连结AC交反比例函数图象于点D. AE为∠BAC的平分线.过点B作AE的垂线，垂足为E，连结DE. 若AC =3DC， △ADE的面积为8，则k的值为 ( )

A、4 B、6 C、8 D、12

查看解析
20、如图，正三角形ABC中，点D、E分别为边AC、AB上的点， BE=2CD，连接DE，过D作DF⊥DE交BC于点F，若要求得△ABC的边长，只要知道( )

A、△ADE的周长 B、△EDF的面积 C、△EDF的周长 D、△BEF的周长

查看解析

上一页 161 162 163 164 165 下一页跳转