相关试卷
- 2017-2018学年人教版数学七年级下册同步训练: 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练:19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练: 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练: 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练:19.2.3《一次函数与方程、不等式》
-
1、 2024年4月,北京大学团队研发出全球最薄的光学晶体-转角菱方氮化硼光学晶体,其厚度仅为米,能效比传统晶体提升了100至1万倍,数据用科学记数法表示为( )A、 B、 C、 D、
-
2、 下列方程中,属于二元一次方程的是( )A、 B、 C、 D、
-
3、 小滨、小江在探索“求代数式的值”时发现,在一定条件下,有些代数式的值始终相等,有些代数式存在最大值或最小值.已知 .
小滨:的值始终等于1.
小江:尽管的值不能被确定,但能求出最小值.其说理过程如下: , 由知,当时,存在最小值2.
(1)、试判断小滨的说法是否正确,并说明理由.(2)、在的条件下,下列代数式:①;②;③;④( , n为整数).(i)值始终保持不变的代数式有: ▲ (填序号);
根据这些代数式的特点,写出一个类似的、值始终保持不变的代数式 ▲ .
(ii)上述分式中是否存在最大值或者最小值,若有,请求出此分式的最大(或最小)值;若没有,请说明理由.
-
4、 生活中我们经常用到密码,如到银行取款.有一种用“因式分解法”产生的密码,方便记忆,其原理是:将一个多项式因式分解,如多项式 , 因式分解的结果为 , 当 , 时,各个因式的值是 , , , 于是就可以把“018162”作为一个六位数密码.(1)、对于多项式 , 当 , 时,试写出用上述方法产生的一个六位数密码.(2)、对于多项式 , 当时,用上述方法产生的其中一个六位数密码为242527,问能否求出p , q , 若能,请求出p , q的值;若不能,请说明理由.
-
5、 某校为了让学生感受祖国的大好河山,计划组织学生参观某景点.该景点面向学生团队出游推出以下优惠活动:
人数x/人
收费标准/元
50
45
40
经核算,若七年级、八年级学生单独组团共需花费11200元;若两个年级学生联合组团只需花费9600元.其中,该校七年级参加入数多于100人、少于200人,八年级参加入数少于100人.问该校七年级、八年级参观该景点的学生人数分别是多少?
-
6、 某校为了更好地了解学生每周的亲子阅读情况,随机抽取部分学生进行问卷调查,并将数据整理成如下的统计表和统计图(不完整).
每周亲子阅读时间的频数表
每周亲子阅读时间扇形统计图
组别
划记
频数
A
正正正正
20
B
正正正正
20
C

12
D
正
5
E
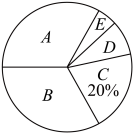
其中,A , B , C , D , E分别表示亲子阅读时间:A:基本没有;B:1小时以内;C:小时;D:小时;E:4小时以上.
(1)、求扇形统计图中E组所对应的圆心角的度数.(2)、若该校共有2400名学生,估计每周亲子阅读时长在3小时及以上的学生人数. -
7、 解方程(组):(1)、(2)、(3)、 .
-
8、 如图, , 点P是的角平分线上一点,且点P在之间,连结 , 设 . 当 , 时,求的度数.

-
9、 分解因式:(1)、 .(2)、 .(3)、 .
-
10、 计算:(1)、 .(2)、 .(3)、 .(4)、 .
-
11、 有两张正方形纸片 , 其中 . 若将这两个正方形纸片按图(1)所示的方式放置(点B和点F重合),产生了一个新的、周长为8的正方形 . 若将这两个正方形纸片按图(2)所示并排放置,其中,点B和点E重合,点A , B , F在同一条直线上,点P是线段的中点.连接 , 若三角形的面积是3.则图(2)中阴影部分的面积是 .

-
12、 已知 , 其中m , n为互不相等实数,且满足 , 则 . (结果用只含a的代数式表示)
-
13、 如图,将一块三角尺沿着方向平移到三角尺的位置,其中,点A的对应点为点D , 连接 . 若 , , 则 .

-
14、 设 , , . 若 , , 则 .
-
15、 在一个样本中,50个数据分别落在5个组内,其中第一、二、四、五组的频率之和为 , 则第三组的频数为 .
-
16、 对于代数式 , 小滨分别计算当 , 2,3,4时该代数式的值,得到以下四个结论:①;②;③;④ . 小江发现其中有且只有一个结论是错误的,则错误的结论是( )A、① B、② C、③ D、④
-
17、 将一条两边互相平行的纸带()按如图方式折叠,折痕分别为 , , 且满足 . 若增大 , 则( )
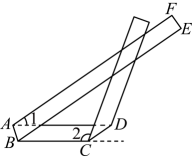 A、增大 B、增大 C、减小 D、减小
A、增大 B、增大 C、减小 D、减小 -
18、 某家具厂设计的餐桌椅套装,1张桌子配4把椅子.该厂一天能生产桌子17张或椅子32把,决定用25天时间生产一批这样的餐桌椅,其中,安排x天只生产桌子,剩余y天只生产椅子.若使生产的桌子和椅子恰好配套,则可列方程组( )A、 B、 C、 D、
-
19、 若实数x满足 , 则的值为( )A、2025 B、2026 C、2027 D、2028
-
20、 在同一平面内,有三条不重合的直线a , b , c , ( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , 则