相关试卷
- 2017-2018学年人教版数学七年级下册同步训练: 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练:19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练: 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练: 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练:19.2.3《一次函数与方程、不等式》
-
1、下列句子中,哪些是命题?哪些不是命题?(1)、 将27开立方;(2)、任意三角形的三条中线相交于一点吗?(3)、锐角小于直角;(4)、 |a|<0(a为实数)。
-
2、写出4个数学名词的定义。
-
3、阅读下面这段叙述:
无人驾驶通过调动感知子系统(由摄像头、激光雷达、全球定位系统和计算机视觉等组成)、决策子系统和执行子系统分工合作,来完成障碍物识别、路标识别、路线规划导航以及驾驶决策等多项任务,从而实现“无人”与“自动驾驶”的最终目标。无人驾驶技术是人工智能技术高度发展的产物,在国防和国民经济领域具有广阔的应用前景。

要读懂这段叙述,你认为哪些名称或术语需给出定义?
-
4、写出四个数学上的命题,并写成“如果……那么……”的形式。
-
5、指出下列命题的条件和结论,并改写成“如果……那么……”的形式.(1)、绝对值相等的两个数相等;(2)、直角三角形的两个锐角互余。
-
6、下列句子中,哪些是命题?哪些不是命题?(1)、正数大于一切负数吗?(2)、两点之间线段最短;(3)、不是无理数;(4)、作一条直线和已知直线垂直。
-
7、给下列各题中的图形命名,并给出名称的定义。(1)、
 (2)、
(2)、 (3)、
(3)、
-
8、指出下列命题的条件和结论,并改写成“如果⋯⋯那么⋯⋯”的形式。(1)、等底等高的两个三角形面积相等;(2)、对顶角相等;(3)、同位角相等,两直线平行。
-
9、说出下列数学名词的定义:(1)、 无理数;(2)、 直角三角形;(3)、 角平分线;(4)、 平方根。
-
10、一个零件图如图。选择合适的比例建立直角坐标系,在直角坐标系中画出这个零件图(只要求画出图形),并求出轮廓线上各个转折点的坐标。

-
11、如图为某次军事演习敌我双方舰艇模拟对峙图。
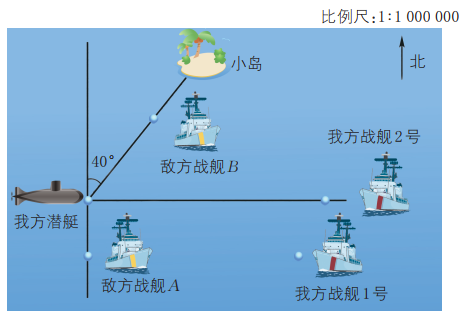 (1)、对于我方潜艇来说,北偏东 方向上有哪些目标?要想确定敌方战舰B的位置,还需要什么数据?这个数据能从图中获取吗?(2)、相对我方潜艇,我方战舰1号在什么位置?(3)、你能用其他方式确定敌我双方战舰的位置吗?
(1)、对于我方潜艇来说,北偏东 方向上有哪些目标?要想确定敌方战舰B的位置,还需要什么数据?这个数据能从图中获取吗?(2)、相对我方潜艇,我方战舰1号在什么位置?(3)、你能用其他方式确定敌我双方战舰的位置吗? -
12、四盏灯笼悬挂点的位置如图。已知点A,C,B,D的坐标分别是(-4,b),(-2.7,b),(-2,b),(2,b),问:平移哪一盏灯,可使得y轴两边的灯笼对称?

-
13、 已知在直角坐标系中,△ABC的三个顶点A,B,C的坐标分别为A(0,-4),B(-4.5,3),C(4.5,5)。(1)、在直角坐标系中画出△ABC。(2)、 以y轴为对称轴,作△ABC的轴对称图形△A'B'C',并写出△A'B'C'各个顶点的坐标。
-
14、 如图, “铅笔”图案五个顶点的坐标分别是(1,1),(4,1),(5,1.5),(4,2),(1,2)。将该图形向下平移2个单位长度,作出相应图形,再写出平移后所得图形五个顶点的坐标。

-
15、如图,直线l上的点的什么坐标都相同?若把直线l上任意一点的坐标记为(-2,y),则把它向右平移5个单位长度所得图形上点的坐标应怎样表示?在直角坐标系中作出这个图形。

-
16、已知在直角坐标系中,点A的坐标是(1.5,2),则点A向右平移2个单位长度后的坐标是 , 点A向下平移3.5个单位长度后的坐标是。
-
17、 填空:(1)、 点P(5,-3)关于x轴对称的点的坐标是;(2)、 点P(3,-5)关于y轴对称的点的坐标是。
-
18、若B地在A地的南偏东30°方向,距离A地30km处,则A地在B地的方向,距离B地处。
-
19、 如图,在直角坐标系中,△ABC的边AB=AC,AB⊥AC。已知点A(-1,0),B(2,2),求点C的坐标。

-
20、 在平面直角坐标系中描出点A(-2,5),B(-3,-1),C(3,-1),D(2,5),依次用线段把它们连起来。说出所连成图形的名称和轴对称性。