相关试卷
- 2017-2018学年人教版数学七年级下册同步训练: 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练:19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练: 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练: 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练:19.2.3《一次函数与方程、不等式》
-
1、根据下列条件,分别判断以a,b,c为边的三角形是不是直角三角形。(1)、 a=7,b=24,c=25;(2)、
-
2、 四根木棒的长度分别为12cm,8cm,5cm,6cm。从中取三根,使它们首尾顺次相接组成一个三角形。一共有多少种取法?把它们都列出来。
-
3、已知平面内三个点A,B,C之间的距离满足关系式AB+BC=AC。画图说明点A,B,C的位置关系.
-
4、如图所示三条线段a,b,c能组成三角形吗?你是用什么方法判别的?
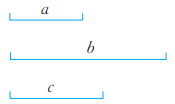
-
5、下列长度的三条线段能组成三角形吗?请说明理由。(1)、 20cm,15cm,8cm;(2)、 7cm,15cm,8cm;(3)、 5cm,15cm,8cm。
-
6、 如图,AC与BE相交于点D。
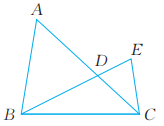 (1)、图中有几个三角形?把它们写出来。(2)、 已知∠ABE=55°,∠EDC=70°,求∠A的度数。
(1)、图中有几个三角形?把它们写出来。(2)、 已知∠ABE=55°,∠EDC=70°,求∠A的度数。 -
7、 如图,在△ABC中,D是AB上一点,且AD=AC,连结CD。在下面各空格中填入“>”或“<”,并说明理由。
 (1)、 ABAC+BC;(2)、 2ADCD。
(1)、 ABAC+BC;(2)、 2ADCD。 -
8、下列长度的三条线段能组成三角形吗?请说明理由。(1)、 1cm,2cm,3.5cm;(2)、 4cm,5cm,9cm;(3)、 6cm,8cm,13cm。
-
9、说出图中的锐角三角形、直角三角形和钝角三角形。
-
10、判断下列各组线段中,哪些首尾顺次相接能组成三角形,哪些不能组成三角形,并说明理由。(1)、 a=2.5cm,b=3cm,c=5cm;(2)、 e=6.3cm,f=6.3cm,g=12.6cm
-
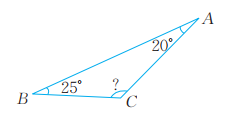
11、计算下面三角形中未知角的度数。这三个三角形的内角有什么特点?(1)、
 (2)、
(2)、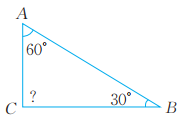 (3)、
(3)、
-
12、说出图中所有的三角形,以及每一个三角形的三条边和三个内角。
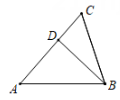
-
13、 如图,AD是△ABC的中线,DE⊥AC,DF⊥AB,E,F分别是垂足。已知AB=2AC,求DE与DF的长度之比。
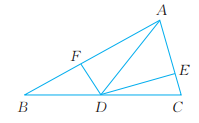
-
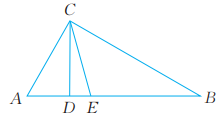
14、 如图,CE是△ABC的角平分线,EF∥BC,交AC于点F。 已知∠AFE=64°,求∠FEC的度数。
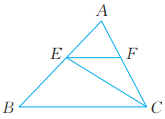
-
15、 如图,在△ABC中,AD是BC边上的中线。已知 5cm,求△ABD与△ACD的周长的差。
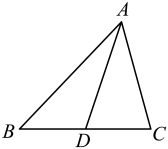
-
16、 如图,在△ABC中,∠ACB=90°,∠B=30°,CD是AB边上的高线,CE是△ABC的角平分线。求∠ECB,∠ECD的大小。
-
17、如图,AD,CE分别是△ABC的中线和角平分线,则:
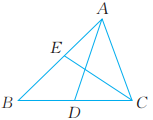
;
.
-
18、(1)、 连结AE。△AEC的面积是多少?(2)、 由第(1)题,你能求出△ECF的面积吗? △ADF和△DBE的面积呢?
-
19、 如图,在△ABC中,AD是BC边上的中线。
 (1)、 △ABC,△ADC有没有共同的高线? 如果有,作出这条高线。(2)、 △ABD与△ADC的面积相等吗? 请说明理由。
(1)、 △ABC,△ADC有没有共同的高线? 如果有,作出这条高线。(2)、 △ABD与△ADC的面积相等吗? 请说明理由。 -
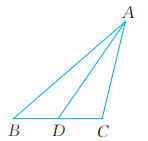
20、 如图,已知△ABC。
 (1)、用刻度尺画BC边上的中线。(2)、用量角器画以C为一个端点的△ABC的角平分线。
(1)、用刻度尺画BC边上的中线。(2)、用量角器画以C为一个端点的△ABC的角平分线。