相关试卷

1、已知 $a > 0 > b$ ，且 $| a | < | b | < 1$ ，那么，以下正确的是（　　）

A、 $1 - b > 1 + a > - b > a$ B、 $1 + a > 1 - b > a > - b$ C、 $1 + a > a > 1 - b > - b$ D、 $1 - b > 1 + a > a > - b$

查看解析
2、已知抛物线 $C : y_{1} = a {(x - h)}^{2} + 2$ ，直线 $l : y_{2} = k x - k h + 2 (k \neq 0)$ ．

(1)、直接写出抛物线 $C$ 的顶点，请问直线 $l$ 是否经过该点？

(2)、若 $a = - 1, h = 1$ ，当 $t \leq x \leq t + 3$ 时，二次函数 $y_{1} = a {(x - h)}^{2} + 2$ 的最大值为 $- 6$ ，求 $t$ 的值；

(3)、点 $P$ 为抛物线的顶点， $Q$ 为抛物线与直线 $l$ 的另一个交点，当 $1 \leq a \leq 3$ 时，若线段 $P Q$ （不含端点 $P, Q$ ）上至少存在一个横坐标为整数的点，求k的取值范围．

查看解析
3、已知抛物线 $y = x^{2} + 2 m x - \frac{5}{4} m^{2} (m > 0)$ ，与 $x$ 轴的交点 $A$ ， $B$ （点 $A$ 在点 $B$ 的左侧）．

(1)、若 $m = 4$ 时，求点 $A$ ， $B$ 的坐标及线段 $A B$ 长．

(2)、若 $A B = 6$ ，求 $m$ 的值及抛物线的对称轴．

查看解析
4、如图，点 $O$ 是等边三角形 $A B C$ 内的一点， $∠ B O C = 150 °$ ，将 $Δ B O C$ 绕点 $C$ 按顺时针旋转得到 $Δ A D C$ ，连接 $O D$ ， $O A$ ．

(1)、求 $∠ O D C$ 的度数；

(2)、若 $O B = 3$ ， $O C = 4$ ，求 $A O$ 的长．

查看解析
5、解方程

(1)、 $x^{2} - x - 1 = 0$

(2)、 $x (x - 2) = 8$

查看解析
6、如图，抛物线 $y = a x^{2} + c$ 与 $x$ 轴交于 $A$ ， $B$ 两点，顶点为 $C$ ，点 $P$ 为抛物线上，且位于 $x$ 轴下方，直线 $P A$ ， $P B$ 与 $y$ 轴分别交于 $E$ ， $F$ 两点，当点 $P$ 运动时， $\frac{O E + O F}{O C} =$ ．

查看解析
7、抛物线 $y = x^{2} - 2 x$ 的顶点坐标是．

查看解析
8、已知关于x的方程 $x^{2} - 3 x + m = 0$ 的一个根是2，则它的另一个根是．

查看解析
9、共享单车计划2021年10、11、12月连续3月对广州投放新型单车，计划10月投放3000台，12月投放6000台，每月按相同的增长率投放，设增长率为x则可列方程（）

A、 $3000 {(1 + x)}^{2} = 6000$ B、 $3000 (1 + x) + 3000 {(1 + x)}^{2} = 6000$ C、 $3000 {(1 - x)}^{2} = 6000$ D、 $3000 + 3000 (1 + x) + 3000 {(1 + x)}^{2} = 6000$

查看解析
10、将 $y = {(x - 1)}^{2} + 3$ 向左平移 $1$ 个单位，再向上平移 $3$ 个单位得到的解析式是（）．

A、 $y = {(x - 2)}^{2}$ B、 $y = {(x - 2)}^{2} + 6$ C、 $y = x^{2}$ D、 $y = x^{2} + 6$

查看解析
11、抛物线 $y = - 2 {(x - 1)}^{2}$ 的顶点坐标和对称轴分别是( )

A、 $(- 1 ， 0)$ ，直线 $x = - 1$ B、 $(1 ， 0)$ ，直线 $x = 1$ C、 $(0 ， 1)$ ，直线 $x = - 1$ D、 $(0 ， 1)$ ，直线 $x = 1$

查看解析
12、下列图形中，既是轴对称图形，又是中心对称图形的是（）．

A、 B、 C、 D、

查看解析
13、综合与实践
背景介绍：勾股定理是几何学中的明珠，充满着魅力．千百年来，人们对它的证明趋之若鹜，其中有著名的数学家，也有业余数学爱好者．向常春在1994年构造发现了一个新的证法．

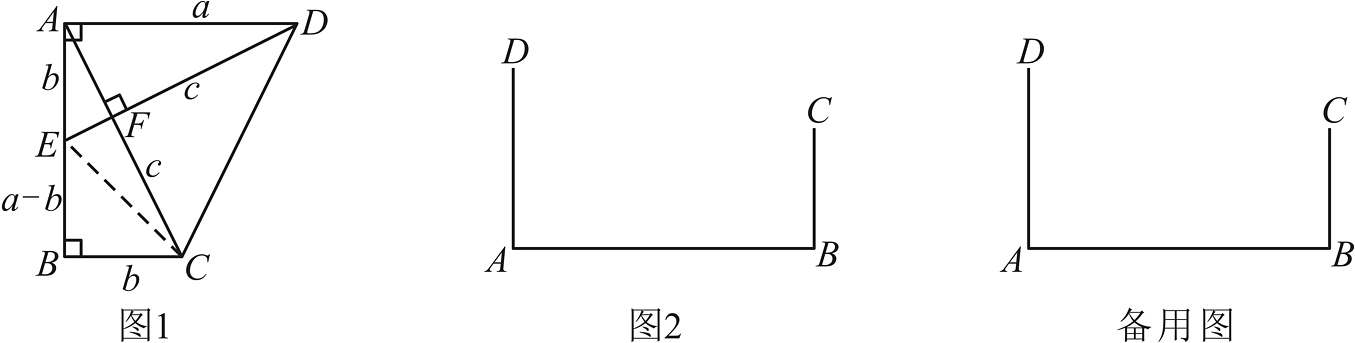(1)、把两个全等的直角三角形如图1放置，其三边长分别为 $a$ 、 $b$ 、 $c$ ．显然， $∠ D A B = ∠ B = 90^{\circ}$ ， $A C ⊥ D E$ ．用含 $a$ 、 $b$ 、 $c$ 的式子分别表示出梯形 $A B C D$ 、四边形 $A E C D$ 、 $△ E B C$ 的面积，再探究这三个图形面积之间的关系，可得到勾股定理．上述图形的面积满足的关系式为________，经化简，可得到勾股定理 $a^{2} + b^{2} = c^{2}$ ．

(2)、如图2，铁路上 $A$ 、 $B$ 两点（看作直线上的两点）相距 $40$ 千米， $C$ 、 $D$ 为两个村庄（看作两个点）， $A D ⊥ A B$ ， $B C ⊥ A B$ ，垂足分别为 $A$ 、 $B$ ， $A D = 24$ 千米， $B C = 16$ 千米，则两个村庄的距离为________千米（直接填空）；

(3)、在（2）的条件下，要在 $A B$ 上建造一个供应站 $P$ ，使得 $P C = P D$ ，求出 $A P$ 的距离．

(4)、借助上面的思考过程与几何模型，求代数式 $\sqrt{x^{2} + 9} + \sqrt{{(16 - x)}^{2} + 81}$ 的最小值 $(0 < x < 16)$ ．

查看解析
14、如图，在平面直角坐标系 $x O y$ 中，点 $A$ 的坐标为 $(- 4, 4)$ ，点 $B$ 的坐标为 $(- 2, 0)$ ，点 $C$ 的坐标为 $(- 1, 2)$ ．

(1)、请画出 $△ A B C$ 关于 $x$ 轴的对称图形 $△ A_{1} B_{1} C_{1}$ ；

(2)、若 $△ A_{2} B_{2} C_{2}$ 与 $△ A_{1} B_{1} C_{1}$ 关于 $y$ 轴对称，请直接写出 $A_{2}$ ， $B_{2}$ ， $C_{2}$ 三点的坐标；

(3)、求 $△ A_{2} B_{2} C_{2}$ 的面积．

查看解析
15、已知 $2 a - 1$ 的算术平方根为3， $3 a + b - 1$ 的立方根为4．

(1)、求 $a$ ， $b$ 的值；

(2)、求 $b - 5 a$ 的平方根．

查看解析
16、解方程：

(1)、 $\frac{1}{9} {(x + 2)}^{2} = 1$

(2)、 $8 {(x - 1)}^{3} + 27 = 0$

查看解析
17、已知 $y = \sqrt{x - 2024} - \sqrt{2024 - x} - 2023$ ，求 $x - y$ 的值．

查看解析
18、已知实数 $a$ ， $b$ 在数轴上的对应点如图所示，化简 $\sqrt{{(a + 2)}^{2}} - \sqrt{{(b - 3)}^{2}} + \sqrt{{(a + b)}^{2}} =$ ．

查看解析
19、如图，把一张长方形纸片 $A B C D$ 折叠起来，使其顶点 $C$ 与 $A$ 重合，折痕为 $E F$ ．若 $A B = 1$ ， $B C = 2$ ，则 $A F$ 长为．

查看解析
20、如图，点A是射线 $B M$ 外一点，连接 $A B$ ，若 $A B = 5 cm$ ，点A到 $B M$ 的距离为 $3 cm$ ，动点P从点B出发沿射线 $B M$ 以 $2 cm/s$ 的速度运动．设运动的时间为t秒，当 $△ A B P$ 为直角三角形时，t的值为（）

A、 $\frac{25}{4}$ B、2 C、2或 $\frac{25}{4}$ D、2或 $\frac{25}{8}$

查看解析

上一页 233 234 235 236 237 下一页跳转