相关试卷

1、如图，某农场老板准备建造一个矩形养兔场 $A B C D$ ，他打算让矩形养兔场的一边完全靠着墙 $M N$ ，墙 $M N$ 可利用的长度为24米，另外三面用长度为50米的篱笆围成（篱笆正好要全部用完，且不考虑接头的部分），设矩形垂直于墙的边 $A B$ 的长为x 米，矩形 $A B C D$ 的面积记为y平方米．

(1)、当 $x = 20$ 时， $B C =$ 米， $y =$ 平方米；

(2)、若要使矩形养兔场的面积为300平方米，则垂直于墙的一边 $A B$ 的长为多少米？

查看解析
2、在如图所示的正方形网格中有 $Rt △ A B C$ ， $∠ C = 90 °$ ， $A C = 4$ ， $B C = 3$ ．

(1)、试在图中作出 $△ A B C$ 以A为旋转中心，沿顺时针方向旋转 $90 °$ 后的图形 $△ A B_{1} C_{1}$ ；

(2)、若点B的坐标为 $(- 3, 4)$ ，点A的坐标为 $(1, 1)$ ， $△ A B_{2} C_{2}$ 是 $△ A B C$ 关于A点中心对称的图形，写出 $B_{2}$ ， $C_{2}$ 两点的坐标．

查看解析
3、若关于x的一元二次方程 $k x^{2} - 2 x - 1 = 0$ 有实数根，则实数k的取值范围是.

查看解析
4、直线 $y = x + m$ 和抛物线 $y = x^{2} + b x + c$ 都经过点 $A (1 ， 0) ， B (3 ， 2)$ ，则不等式 $x^{2} + b x + c > x + m$ 的解集为（　　）

A、 $0 < x < 2$ B、 $x < 2$ C、 $0 < x < 3$ D、 $x < 1$ 或 $x > 3$

查看解析
5、将一元二次方程 $x^{2} - 8 x - 5 = 0$ 化成 ${(x + a)}^{2} = b$ （a，b为常数）的形式，则a，b的值分别是（）

A、 $- 4, 21$ B、 $- 4, 11$ C、4，21 D、 $4, - 21$

查看解析
6、2024年巴黎奥运会顺利闭幕，吉样物“弗里热”深受奥运迷的喜爱，一商场以20元的进价进一批“弗里热”纪念品，以40元每个的价格售出，每周可以卖出500个，经过市场调查发现，价格每涨1元，就少卖10个．

(1)、若商场计划一周的利润达到 $12000$ 元，并且更大优惠让利消费者，售价应定为多少钱？

(2)、商场改变销售策略，在不改变（1）的销售价格基础上，销售量稳步提升，两周后销售量达到了484个，求这两周的平均增长率．

查看解析
7、从地面竖直向上发射的物体离地面的高度 $h (m)$ 满足关系式 $h = - 5 t^{2} + v_{0} t$ ，其中 $t (s)$ 是物体运动的时间， $v_{0} (m / s)$ 是物体被发射时的速度．社团活动时，科学小组在实验楼前从地面竖直向上发射小球．

(1)、小球被发射后_________ $s$ 时离地面的高度最大（用含 $v_{0}$ 的式子表示）．

(2)、若小球离地面的最大高度为 $20 m$ ，求小球被发射时的速度．

(3)、按（2）中的速度发射小球，小球离地面的高度有两次与实验楼的高度相同．小明说：“这两次间隔的时间为 $3 s$ ． ”已知实验楼高 $15 m$ ，请判断他的说法是否正确，并说明理由．

查看解析
8、已知二次函数 $y = - x^{2} + x + 6$ ，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新的函数图象（如图所示），当直线 $y = - x + m$ 与新图象有3个交点时，m的值是．

查看解析
9、如图， $△ A B C$ 内接于 $⊙ O$ ， $∠ A = 45 °$ ， $B C = 6$ ，则 $⊙ O$ 的直径为．

查看解析
10、如图1， $△ A B C$ 是等边三角形，点 $D$ 在边 $A B$ 上， $B D = 2$ ，动点 $P$ 以每秒1个单位长度的速度从点 $B$ 出发，沿折线 $B C - C A$ 匀速运动，到达点 $A$ 后停止，连接 $D P$ ．设点 $P$ 的运动时间为 $t (s)$ ， $D P^{2}$ 为 $y$ ．当动点 $P$ 沿 $B C$ 匀速运动到点 $C$ 时， $y$ 与 $t$ 的函数图象如图2所示．有以下三个结论：① $A B = 3$ ；②当 $t = 5$ 时， $y = 1$ ；③当 $4 \leq t \leq 6$ 时， $1 \leq y \leq 3$ ；正确的有（）

A、①②③ B、②③ C、③④ D、①②

查看解析
11、计算： $- 3^{2} - (- 1 \frac{1}{2}) \times \frac{2}{3} - 6 \div |- \frac{1}{3}|$

查看解析
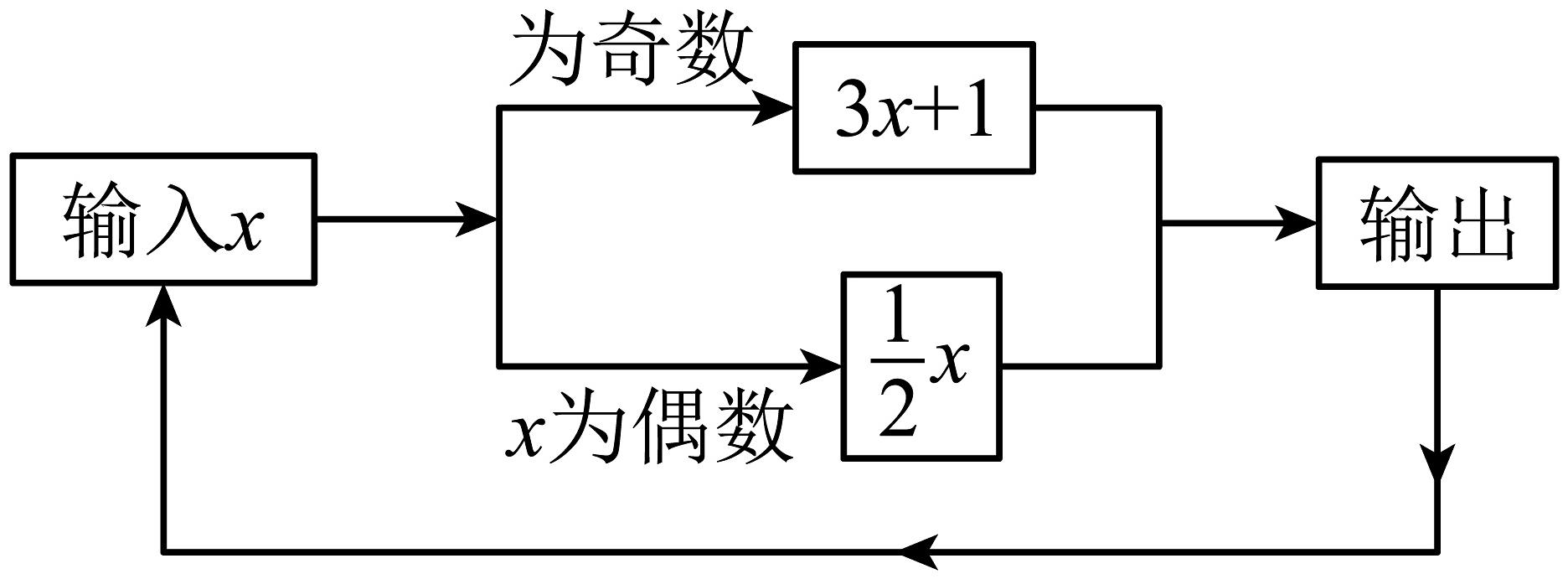
12、有一个数值转换器，原理如图所示，若开始输入 $x$ 的值是5，可发现第1次输出的结果是16，第2次输出的结果是8，第3次输出的结果是4，依次继续下去，第2025次输出的结果是．

查看解析
13、已知 $- 2 x^{6} y$ 与 $5 x^{2 m} y^{n}$ 是同类项，则 $m - n =$ ．

查看解析
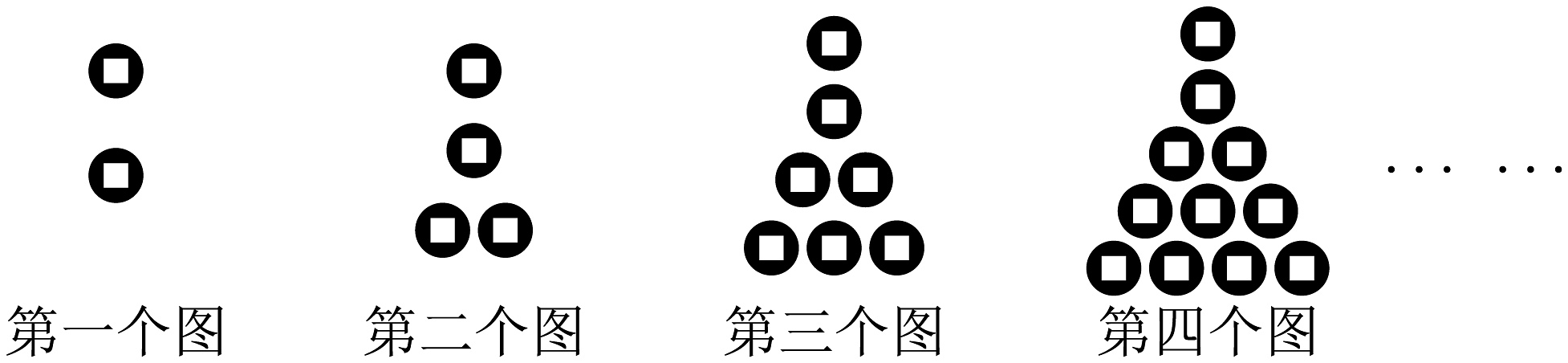
14、如图图形是用同样大小的铜币摆放的四个图案，根据摆放图案的规律，则第8个图案需要铜币的个数为（　　）

A、29 B、36 C、37 D、46

查看解析
15、已知 $a^{2} + 3 a = 2$ ，则多项式 $2 a^{2} + 6 a - 10$ 的值为（）

A、6 B、 $- 6$ C、 $- 14$ D、14

查看解析
16、下列说法正确的是（）

A、绝对值等于本身的数是正数 B、在数轴上离原点越远的数越大 C、两个数中，较大的那个数的绝对值较大 D、相反数等于本身的数是0

查看解析
17、据揭阳移动大数据监测，今年国庆假期，全市总游客量达165.03万人次，165.03万用科学记数法表示是（）

A、 $165.03 \times 10^{4}$ B、 $16.503 \times 10^{5}$ C、 $1.6503 \times 10^{6}$ D、 $0.16503 \times 10^{7}$

查看解析
18、如图1，已知点A，B，C在数轴上对应的数分别是a，b，c，其中a，b满足 ${(a + 20)}^{2} + |b - 16| = 0$ ，点C到原点O的距离与点A到原点O的距离相等，点A，B之间的距离记为 $A B$ ．

(1)、直接写出a，b，c的值；

(2)、点P从点A出发，沿着数轴负方向匀速运动，同时，点Q从点C出发，沿数轴负方向匀速运动，点Р和点Q的速度分别为4个单位长度/秒和 $m (m > 4)$ 个单位长度/秒．设点P运动的时间为t秒．
①t秒时，点P表示的数为______，点B，P之间的距离为_________；
②当点Q追上点P之后， $C P - \frac{3}{2} P Q$ 的值与t的值无关，求m的值．

(3)、点G在数轴上， $O G = B G$ ，将数轴在点O，G，B各折一下，得到如图2的“折线数轴”．点M从点A出发沿着“折线数轴”运动至点C，同时点N从点C出发沿着“折线数轴”向点A运动，点M，N的初始速度分别为4个单位长度/秒和2个单位长度/秒，两点运动到折线时速度才会发生变化，“上坡”时速度为初始速度一半，“下坡”时速度为初始速度2倍，离开折线OGB后速度恢复为初始速度．当点M和点N相遇时，直接写出此时点M表示的数．

查看解析
19、综合与实践二维码在日常生活中应用广泛，使用若干个与二进制相对应的几何图形来表示数值（黑色代表1，白色代表0）．如图1，是小明同学的准考证号的二维码的简易编码，其中第一行代表二进制的数字 ${(11000)}_{2}$ ，转换成十进制数为24；同理第二行至第五行代表二进制的数字分别转换成十进制的两位数，依次组合到一起就是小明同学的准考证号2412072813．

(1)、图2是小辉同学的准考证号的二维码的简易编码．
①直接写出第一行，第二行分别代表二进制的数字；
②直接写出小辉同学的准考证号；
③若将第一行至第五行代表的5个二进制的数字相加，直接写出用二进制数与四进制数分别表示这5个数字的和．

(2)、二维码不仅能储存数字信息，还能通过代码将数字信息转换成字母语言信息．
将大写英文26个字母作为明码，它对应数字暗码如下表：
明码
A
B
C
D
E
F
G
H
I
J
K
L
M
暗码
1
2
3
4
5
6
7
8
9
10
11
12
13
明码
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
暗码
14
15
16
17
18
19
20
21
22
23
24
25
26
若二维码的简易编码所对应的数值m小于27，则设 $27 - m$ 的值为二维码的简易编码所对应暗码，若二维码的简易编码所对应的数值m大于或等于27，则二维码的简易编码所对应的明码为空格，如图1中第一列所对应的二进制的数字10010转换成十进制数18，则暗码为 $27 - m = 27 - 18 = 9$ ，则对应的明码为“Ⅰ”，第二列中所对应的二进制的数字11011转换成十进制数27，则此时二维码的简易编码所对应的明码为空格．
①直接写出图2中从左到右五列对应的明码分别是什么？
②请在图3中画出一个明码为“LUCKY”的 $5 \times 5$ 的二维码．

查看解析
20、列代数式．

(1)、糖果厂生产一批水果糖．把这些水果糖平均分装在若干袋子里，每袋装的颗数和总袋数如下表所示．
每袋装的颗数
10
12
18
20
24
…
总袋数
360
300
200
180
150
…
这批水果糖共有_______颗；用n表示总袋数，m表示每袋装的颗数，用式子表示n与m的关系是___．

(2)、甲、乙两地之间公路全长 $240$ km，汽车从甲地开往乙地，原计划行驶速度为 $v km/h$ ．
①若汽车速度增加 $10km/h$ ，那么汽车从甲地到乙地需要行驶______小时；汽车比原计划早到_____小时．
②若出发的第1小时以 $v km/h$ 匀速行驶，1小时后速度增加 $10km/h$ 继续行驶至乙地，汽车比原计划早到_________小时．

(3)、现存于陕西历史博物馆的我国南北朝时期的官员独孤信的印章的示意图如图所示，它由18个相同的正方形和8个相同的等边三角形围成．如果其中正方形和等边三角形的边长都为a，等边三角形的高为b，那么这个印章的表面积为________；这个印章所有棱长的和为_______．

查看解析

上一页 986 987 988 989 990 下一页跳转

明码	A	B	C	D	E	F	G	H	I	J	K	L	M
暗码	1	2	3	4	5	6	7	8	9	10	11	12	13
明码	N	O	P	Q	R	S	T	U	V	W	X	Y	Z
暗码	14	15	16	17	18	19	20	21	22	23	24	25	26

每袋装的颗数	10	12	18	20	24	…
总袋数	360	300	200	180	150	…