相关试卷

1、九年级学生小林进行跨学科自主学习活动，他利用函数的相关知识在实验场景 $A$ 和实验场景 $B$ 下做对比，研究某种化学试剂的挥发情况，若当实验过程中该试剂挥发时间为 $x$ 分钟时，在实验场景 $A$ ， $B$ 中的剩余质量分别为 $y_{1}$ ， $y_{2}$ （单位：克）记录 $y_{1}$ ， $y_{2}$ 与 $x$ 的几组对应值如下：
$x$ （分钟）
0
5
10
15
20
…
$y_{1}$ （克）
25
23.5
20
14.5
7
…
$y_{2}$ （克）
25
20
15
10
5
…
请你协助小林将探究过程补充完整：

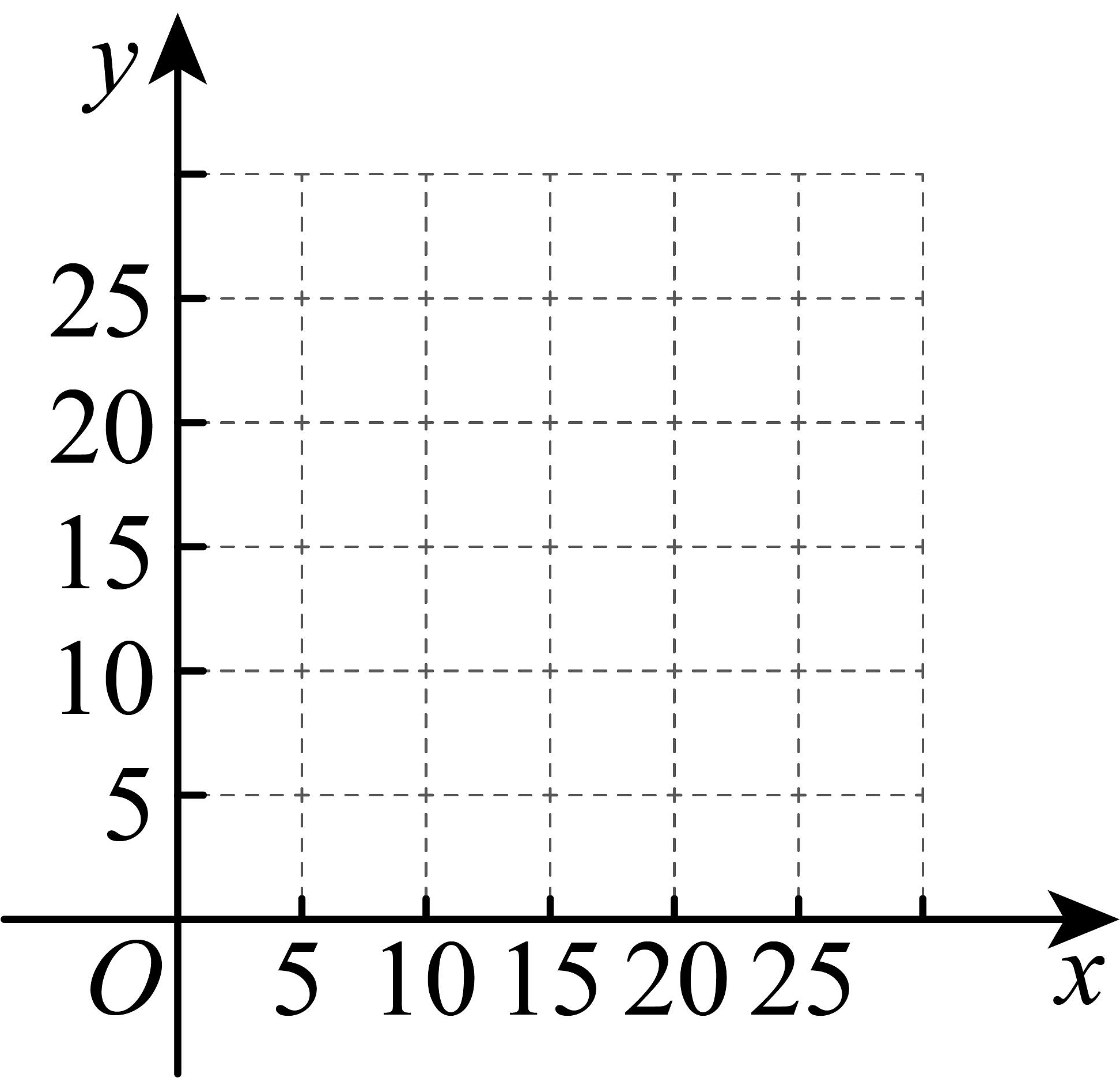(1)、在同一平面直角坐标系 $x O y$ 中，描出上表中各组数值所对应的点 $(x, y_{1})$ ， $(x, y_{2})$ 并画出函数 $y_{1}$ ， $y_{2}$ 的图象；

(2)、进一步探究发现，实验场景 $A$ 的图象是抛物线的一部分， $y_{1}$ 与 $x$ 之间近似满足二次函数： $y_{1} = a x^{2} - 0.1 x + c$ ；实验场景 $B$ 的图象是直线的一部分， $y_{2}$ 与 $x$ 之间近似满足一次函数 $y_{2} = k x + 25$ ，则 $a =$ ___________， $c =$ ___________， $k =$ ___________；

(3)、查阅文献可知，该化学试剂的质量不低于5克时，才能发挥有效作用，在上述实验中，记该化学试剂在场景 $A$ ， $B$ 中发挥有效作用的时间分别为 $x_{A}$ ， $x_{B}$ ，则 $x_{A}$ ___________ $x_{B}$ （填“>”，“=”或“<”）．

查看解析
2、已知抛物线 $y = x^{2} - 4 a x + 4 a^{2} + 3$ （ $a$ 是常数）

(1)、当 $a = 1$ 时，求该抛物线的顶点坐标；

(2)、证明：不论 $a$ 为何值，该抛物线与 $x$ 轴没有交点．

查看解析
3、在平面直角坐标系中， $△ A B C$ 的三个顶点坐标分别为 $A (1, 2)$ ， $B (4, 3)$ ， $C (2, 0)$ ．

(1)、画出 $△ A B C$ 关于 $x$ 轴对称的 $△ A_{1} B_{1} C_{1}$ ；

(2)、以原点为位似中心，在网格中画出（1）中 $△ A_{1} B_{1} C_{1}$ 的位似图形 $△ A_{2} B_{2} C_{2}$ ，使 $△ A_{2} B_{2} C_{2}$ 与 $△ A_{1} B_{1} C_{1}$ 的相似比为 $3 : 1$ ．

查看解析
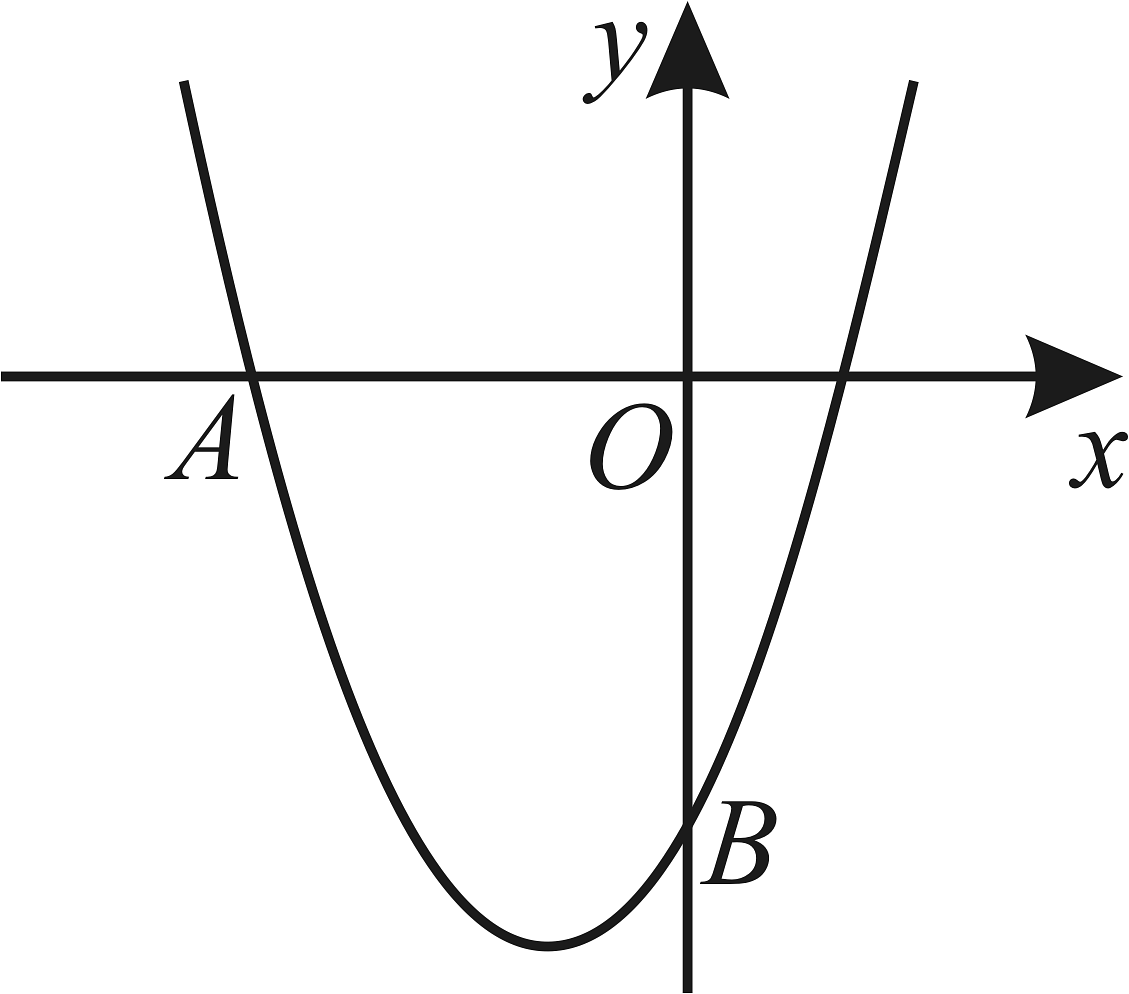
4、如图，抛物线 $y = x^{2} + b x + c$ （b，c是常数）与x轴负半轴、y轴负半轴分别交于点A和点B，已知 $O A = O B = 3$ ．求 $b$ ， $c$ 的值．

查看解析
5、如图，在矩形 $A B C D$ 的边 $B C$ 上取一点 $G$ ，使得 $B G = B A$ ，点 $E$ 是 $B G$ 上一点，以 $A E$ 为直角边作等腰 $Rt △ A E F$ ， $A E = E F$ ．连接 $G F$ 并延长交 $A D$ 于点 $H$ ．
（1）若 $∠ E A G = 10 °$ ，则 $∠ A F G$ 的度数为°；
（2）连接 $C F$ ，若 $A B = 4$ ， $A D = 10$ ，则 $C F$ 的最小值为．

查看解析
6、如图，某公园的示意图是对角线互相垂直的四边形 $A B C D$ ，已知 $A C + B D = 160$ 米，则该四边形公园的最大面积为平方米．

查看解析
7、如图，已知 $∠ A B C = ∠ A C D = 90 °$ ，补充一个条件： $\frac{A B}{A C} =$ ，可使 $△ A B C ∽ △ D C A$ ．

查看解析
8、将抛物线 $y = 4 {(x - 3)}^{2} + 2$ 向左平移 $3$ 个单位，再向下平移 $1$ 个单位后得到的抛物线的函数表达式为．

查看解析
9、如图，正方形 $A B C D$ 的边长为 $4 cm$ ，点 $G$ 和点 $H$ 分别沿着路线 $A \to B \to C$ 和 $C \to D$ 同时运动，点 $G$ 和点 $H$ 的运动速度分别为 $2 cm / s$ 、 $1 cm / s$ ，当点 $G$ 运动到点 $C$ 时，两点同时停止运动，连接 $C G$ ， $H G$ ，设 $△ C G H$ 的面积为 $s ({cm}^{2})$ ，运动时间为 $t (s)$ ， $s$ 和 $t$ 之间的函数关系图象大致为（　　）

A、 B、 C、 D、

查看解析
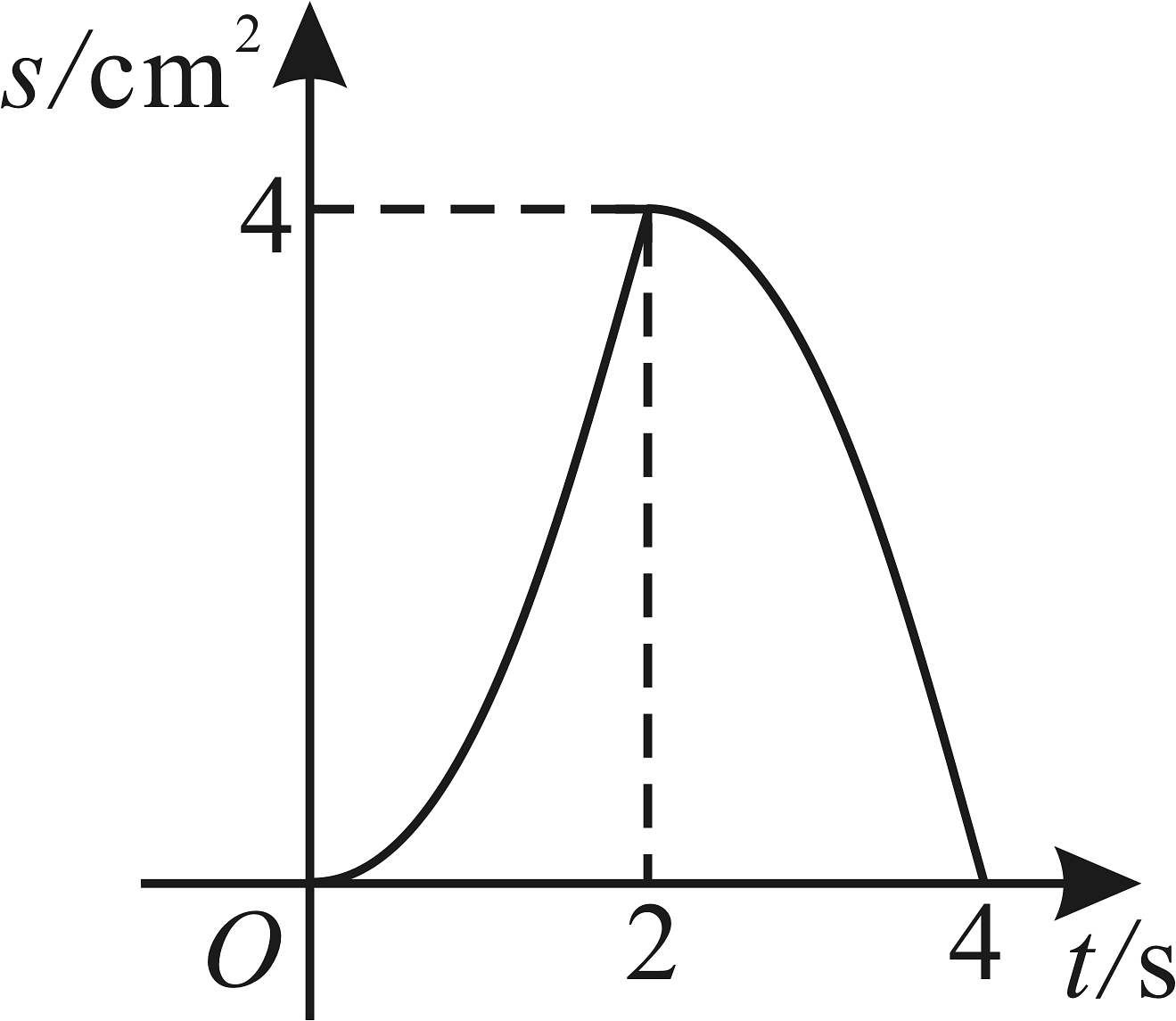
10、如图，点A，B都是双曲线 $y = \frac{k}{x} (k \neq 0, x > 0)$ 上的点，连接 $A B$ 并延长交x轴于点C，已知 $△ A O C$ 的面积为12， $A B = 2 B C$ ，则k的值为（）

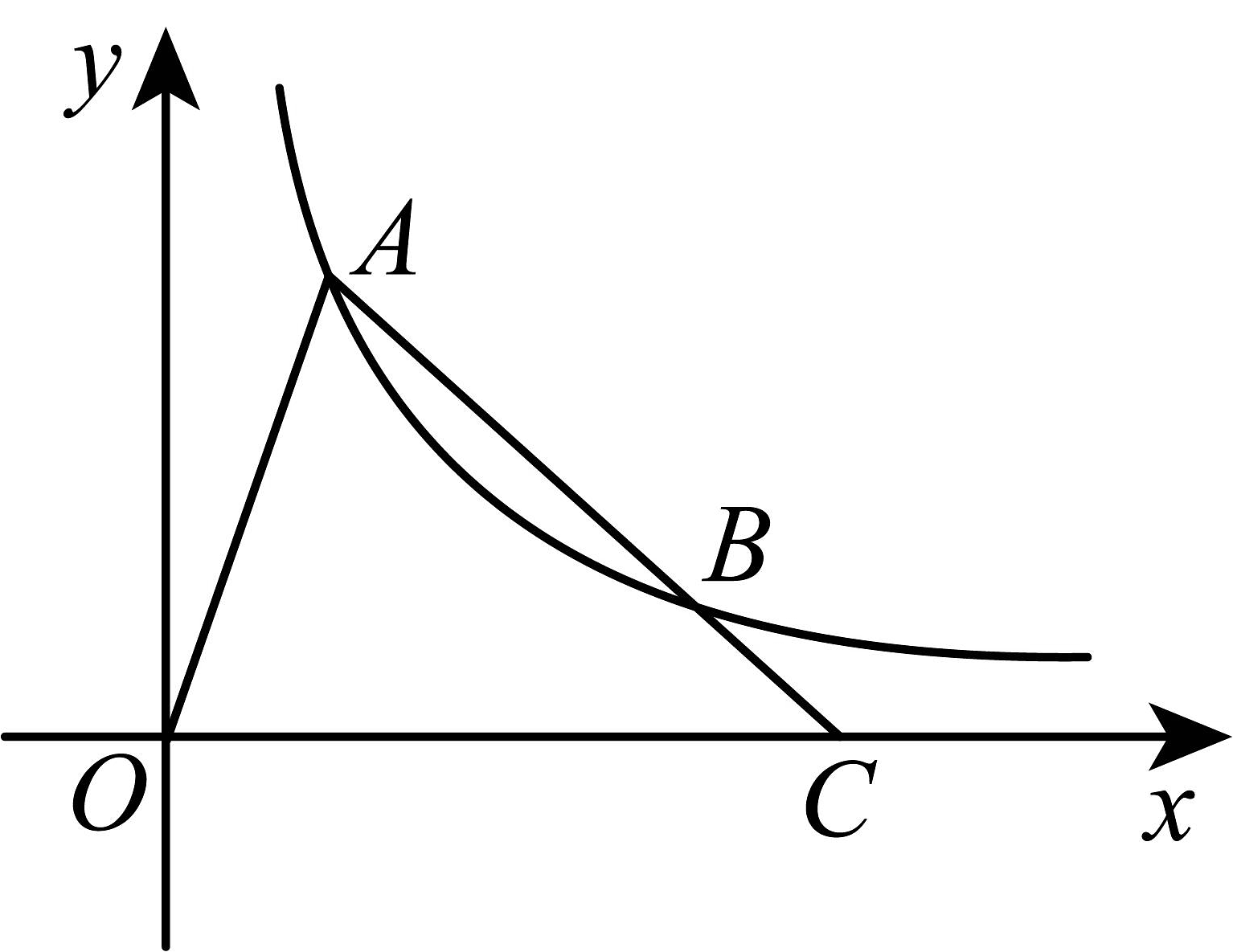A、3 B、4 C、5 D、6

查看解析
11、在平面直角坐标系中，抛物线 $y = 4 {(x + 2)}^{2} - 3$ 经过 $A (- 3, a)$ 、 $B (0, b)$ 、 $C (1, c)$ 三点，则 $a$ ， $b$ ， $c$ 的大小关系是（　　）

A、 $b < c < a$ B、 $a < b < c$ C、 $c < b < c$ D、 $a < c < b$

查看解析
12、如图，在一片树叶中， $P$ 为 $A B$ 的黄金分割点 $(A P > B P)$ ，如果 $A B$ 的长度为 $12 cm$ ，那么较短线段 $B P$ 的长度为（　　）

A、 $(\sqrt{5} + 1) cm$ B、 $(6 \sqrt{5} - 12) cm$ C、 $(6 \sqrt{5} - 6) cm$ D、 $(18 - 6 \sqrt{5}) cm$

查看解析
13、如图，在 $△ A B C$ 中，点 $D$ 是 $A C$ 上一点，下列条件不能判定 $△ A B D ∽ △ A C B$ 的是（　　）

A、 $∠ A B D = ∠ A C B$ B、 $∠ A D B = ∠ A B C$ C、 $\frac{D B}{A B} = \frac{B C}{A C}$ D、 $\frac{A D}{A B} = \frac{A B}{A C}$

查看解析
14、若反比例函数 $y = \frac{6 - 2 k}{x}$ 的图象在第二、四象限，则 $k$ 的值可以是（　　）

A、1 B、2 C、3 D、4

查看解析
15、如图， $A F ∥ B E ∥ C D$ ，已知 $\frac{A B}{B C} = \frac{2}{3}$ ， $D F = 10$ ，则 $D E$ 的值为（　　）

A、4 B、6 C、7 D、8

查看解析
16、抛物线 $y = - {(x + 3)}^{2} - 1$ 的开口方向和顶点坐标分别是（　　）

A、开口向下， $(- 3, - 1)$ B、开口向上， $(3, - 1)$ C、开口向下， $(- 3, 1)$ D、开口向上， $(- 3, 1)$

查看解析
17、若 $\frac{n}{m} = \frac{1}{4}$ ，则 $\frac{m}{m + n}$ 的值为（　　）

A、 $\frac{2}{3}$ B、 $\frac{3}{4}$ C、 $\frac{4}{5}$ D、 $\frac{5}{6}$

查看解析
18、观察下列等式： $7^{0} = 1$ ， $7^{1} = 7$ ， $7^{2} = 49$ ， $7^{3} = 343$ ， $7^{4} = 2401$ ， $7^{5} = 16807$ ， …根据其中的规律可得 $7^{0} + 7^{1} + 7^{2} + \dots + 7^{2025}$ 的结果的个位数字是．

查看解析
19、已知某二次函数的图象的顶点坐标为 $(3, - 4)$ ，且图象经过点 $(0, 5)$ ．

(1)、求该二次函数的解析式；

(2)、当 $2 \leq x \leq t$ 时，该二次函数的最大值与最小值的差是8，求t的值；

(3)、已知点 $M (2, m)$ ， $N (5, - 4)$ ，若该二次函数的图象与线段 $M N$ 只有一个公共点，请求出m的取值范围．

查看解析
20、已知抛物线 $y = - \frac{1}{2} x^{2} + \frac{1}{2} x + 3$ ．

(1)、图象的开口方向为_______，对称轴是_______，顶点坐标是_______．

(2)、分别求出抛物线与x轴，y轴的交点坐标．

(3)、在给出的平面直角坐标系中，作出（1）（2）中的点和线

(4)、观察图象：当 $- \frac{1}{2} x^{2} + \frac{1}{2} x + 3 \geq 0$ 时，x的取值范围为_______；当 $- 3 \leq x \leq 2$ 时，y的最小值为_______，最大值为_______．

查看解析

上一页 985 986 987 988 989 下一页跳转

$x$ （分钟）	0	5	10	15	20	…
$y_{1}$ （克）	25	23.5	20	14.5	7	…
$y_{2}$ （克）	25	20	15	10	5	…