-
1、如图,在四边形ABCD中,点 E 是BC的中点,连接AC,DE,交于点 F,且∠AFD=∠B.若CE=2,AC=5,则下列结论正确的是( )
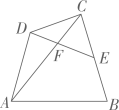 A、AB:EF=5:3 B、 C、 D、△CEF∽△CAB
A、AB:EF=5:3 B、 C、 D、△CEF∽△CAB -
2、 如图,在△ABC中,点 D,E分别在边AB,AC上,连接DE,且DE∥BC,若AD=3,AB=4,S四边形DECB=14,则S△ABC= ( )
 A、50 B、40 C、32 D、26
A、50 B、40 C、32 D、26 -
3、如图,在Rt△ABC中, 点D是AB边上的点, 交AC于点E, AB=10,则BC的长为.

-
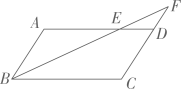
4、如图,在▱ABCD中,点E 在边AD上,连接BE并延长交CD的延长线于点F,若AE=2ED,DE∥BC则FD:FC的值为.
-
5、已知 , 互为倒数, , 互为相反数, , 求的值.
-
6、先化简,再求值: . 其中 , .
-
7、计算:(1)、(2)、(3)、(4)、
-
8、如图所示的日历中,带阴影的方框里有四个数,随着方框的移动,方框里的四个数存在一定的关系.设方框里最小的一个数为 , 则这四个数之和为(用含的代数式表示,并化为最简).

-
9、计算的结果是 .
-
10、在数轴上与相距3个单位长度的点有个,它们分别是和 .
-
11、如图,数轴上有、两点(O为原点),两点距离为9个数轴单位长度,动点、分别从、两点同时出发,向右运动,点的速度为3个单位长度/ , 点的速度为1个单位长度 , 设运动时间为 , 若点、两点之间的距离为7个单位长度,则t为( )
 A、 B、 C、或 D、或
A、 B、 C、或 D、或 -
12、下列从左到右的变形错误的是( )A、 B、 C、 D、
-
13、下列关于多项式的说法正确的是( )A、由 , 2x,1三项组成 B、三项系数分别为3, , C、是三次三项式 D、常数项为1
-
14、如果 , 那么的值是( )A、 B、2019 C、 D、1
-
15、用四舍五入法对取近似值,并精确到的结果为( )A、 B、 C、 D、
-
16、某天的温度上升的意义是( )A、下降了 B、上升了 C、下降了 D、没有变化
-
17、【概念学习】
规定:求若干个相同的有理数均不等的除法运算叫做除方,如 , 等类比有理数的乘方,我们把记作 , 读作“的圈次方”,记作 , 读作“的圈次方”.
一般地,把记作 , 读作“的圈次方”.
【初步探究】
(1)直接写出计算结果: .
【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,那有理数的除方运算也可以转化为乘方运算.

(2)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
; .
(3)将一个非零有理数的圈次方写成幂的形式: .
(4)利用(3)的结论计算:
-
18、【问题背景】
(1)“整体思想”是中学数学解题中一种重要的思想方法,应用极为广泛.例如:已知 , 求代数式 的值;
【尝试运用】
(2)已知 , 求 的值;
(3)已知 求代数式 的值.
-
19、小亮房间窗户的窗帘装饰如图(1)所示,它由两个四分之一圆组成(半径相同).
 (1)、用代数式表示图(1)中窗户能射进阳光的面积(窗框面积不计)(结果保留π);(2)、当 , 时,窗户能射进阳光的面积是多少?(π取3)(3)、小亮又设计了如图(2)的窗帘装饰,它由四个半圆组成(半径都相同).哪种设计方案窗户射进阳光的面积大?请说明理由
(1)、用代数式表示图(1)中窗户能射进阳光的面积(窗框面积不计)(结果保留π);(2)、当 , 时,窗户能射进阳光的面积是多少?(π取3)(3)、小亮又设计了如图(2)的窗帘装饰,它由四个半圆组成(半径都相同).哪种设计方案窗户射进阳光的面积大?请说明理由 -
20、天干地支纪年法,源于中国,中国自古便有十天干与十二地支.十天干即:甲、乙、丙、丁、戊、己、庚、辛、壬、癸;十二地支即:子、丑、寅、卯、辰、 巳、午,未、 申、酉、戌、亥 .天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,以此类推.排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”,“乙亥”,之后地支回到“子”重新开始,即“丙子”,以此类推,中华人民共和国成立的1949年是己丑年,今年是2024年,也是伟大的中华人民共和国成立75周年,则2024年是年.(用天干地支纪年法表示)