相关试卷

1、如图，点A ， B ， C ， D在⊙O上，BD是直径， $∠ B A C = 45 °$ ，过点C作CE∥BD交AB的延长线于点E.

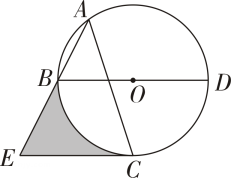(1)、求证：CE是⊙O的切线.

(2)、若 $B D = 4 ∠ A B D = 2$ ，求图中阴影部分的面积.

查看解析
2、某校开展“中国诗词”竞赛，学生成绩为正整数，满分为5分.为了解本次竞赛的情况，从该校随机抽取m名学生的成绩作为样本，将收集的数据整理并绘制成如下两幅不完整的统计图.根据以上信息，解答下列问题：

(1)、m的值是，扇形统计图中“5分”对应的扇形的圆心角大小是.

(2)、该校共有1000名学生参加竞赛，估计成绩超过3分的学生人数.

(3)、从样本的众数、中位数中选择一个统计量，写出它的值并说明它的实际意义.

查看解析
3、如图，四边形ABCD的对角线交于点O ， AD∥BC.若 ▲ ，则AD=CB
从①OA=OC ， ②∠ABC=∠CDA ， ③AB=CD这三个选项中选择一个作为条件，使结论成立，并说明理由.

查看解析
4、解不等式组 ${\begin{cases} 3 x - 5 \leq 1 ① \\ 2 x + 1 ＞ x ② \end{cases}$

查看解析
5、已知二次函数y= ax²+(a-2)x-2(a为常数，且a≠0).下列五个结论：
①该函数图象经过点(-1，0)；
②若a=-1，则当x＞-1时，y随x的增大而减小；
③该函数图象与x轴有两个不同的公共点；
④若a＞2，则关于x的方程.ax²+(a-2)x-2=0有一个根大于0且小于1；
⑤若a＞2，则关于x的方程 | ax²+(a-2)x-2|=2的正数根只有一个.
其中正确的是(填写序号).

查看解析
6、如图，在△ABC中，AB=AC=10，BC=2 $\sqrt{10}$ ，点D在边AC上，CD=3.若点E在边AB上，满足CE=BD ，则AE的长是.

查看解析
7、某科技小组用无人机测量一池塘水面两端A ， B的距离，具体过程如下：如图，将无人机垂直上升至距水面120m的P处，测得A处的俯角为 45°B处的俯角为 22°，则A ， B之间的距离是m.(tan22°取0.4)

查看解析
8、方程 $\frac{1}{x - 1} = \frac{4}{x^{2} - 1}$ 的解是.

查看解析
9、在平面直角坐标系中，某反比例函数 $y = \frac{k}{x}$ 的图象分别位于第一、第三象限.写出一个满足条件的k的值是.

查看解析
10、在标准大气压下，四种物质的凝固点如下表所示，其中凝固点最低的物质是.
物质
铁
酒精
液态氧
水
凝固点(单位：℃)
1535
-117
-218
0

查看解析
11、如图1，在△ABC中，D是边AC上的定点.点P从点A出发，依次沿AB ， BC两边匀速运动，运动到点C时停止.设点P运动的路程为x ， DP的长为y ， y关于x的函数图象如图2所示.其中M ， N分别是两段曲线的最低点.点N的纵坐标是( )

A、 $\frac{116}{17}$ B、 $\frac{120}{17}$ C、 $\frac{112}{15}$ D、 $\frac{116}{15}$

查看解析
12、如图，四边形ABCD内接于⊙O ， . $\overset{⌢}{A B} = 2 \overset{⌢}{C D}$ 若 AB=6，CD= $\sqrt{13}$ ，则⊙O的半径是（）

A、 $\frac{13}{4}$ B、 $\frac{7}{2}$ C、 $\frac{9}{2}$ D、5

查看解析
13、如图，在△ABC中，AB=AC ， D是边AB上的点，将△BCD沿直线CD折叠，点B的对应点E恰好落在边AC上.若∠A=34°，则∠ADE的大小是( )

A、35° B、37° C、39° D、41°

查看解析
14、某商场开展购物抽奖促销活动，抽奖盒中装有三个小球，它们分别标有10元、20元、30元，一次性随机摸出两个小球，摸出的两球上金额的和为50元的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看解析
15、“漏壶”是中国古代一种全天候计时仪器，在它内部盛一定量的水，水从壶下的小孔漏出，壶内壁有刻度.人们根据壶中水面的位置计算时间.壶中水面高度y(单位：cm)随漏水时间t(单位：h)的变化规律如图所示(不考虑水量变化对压力的影响).水面高度从48cm变化到42cm所用的时间是( )

A、3h B、4h C、6h D、12h

查看解析
16、下列计算正确的是( )

A、 $a^{2} + a^{3} = a^{5}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 $(- a^{3})^{2} = a^{6}$ D、 $a^{8} \div a^{2} = a^{4}$

查看解析
17、 2025年“五一”期间，全国旅游市场火爆.据文化和旅游部数据中心统计，国内旅游消费超过1800亿元(1亿=10⁸)，同比增长8%.将数据1800亿用科学记数法表示是（）

A、0.18 x 10¹² B、1.8 x 10¹¹ C、18 x 10¹⁰ D、1.8x 10¹²

查看解析
18、如图是由五个相同的小正方体组成的几何体，它的俯视图是( )

A、 B、 C、 D、

查看解析
19、掷两个质地均匀的小正方体，小正方体的六个面上分别标有1到6的数字.下列事件是必然事件的是( )

A、向上两面的数字和为5 B、向上两面的数字和大于1 C、向上两面的数字和大于12 D、向上两面的数字和为偶数

查看解析
20、现实世界中，对称现象无处不在，中国的方块字中有些也具有对称性.下列美术字是轴对称图形的是( )

A、 B、 C、 D、

查看解析

上一页 848 849 850 851 852 下一页跳转

物质	铁	酒精	液态氧	水
凝固点(单位：℃)	1535	-117	-218	0