-
1、将个边长都为的正方形按如图所示的方法摆放,点 , , …,分别是正方形对角线的交点,则个正方形重叠形成的重叠部分的面积和为( )
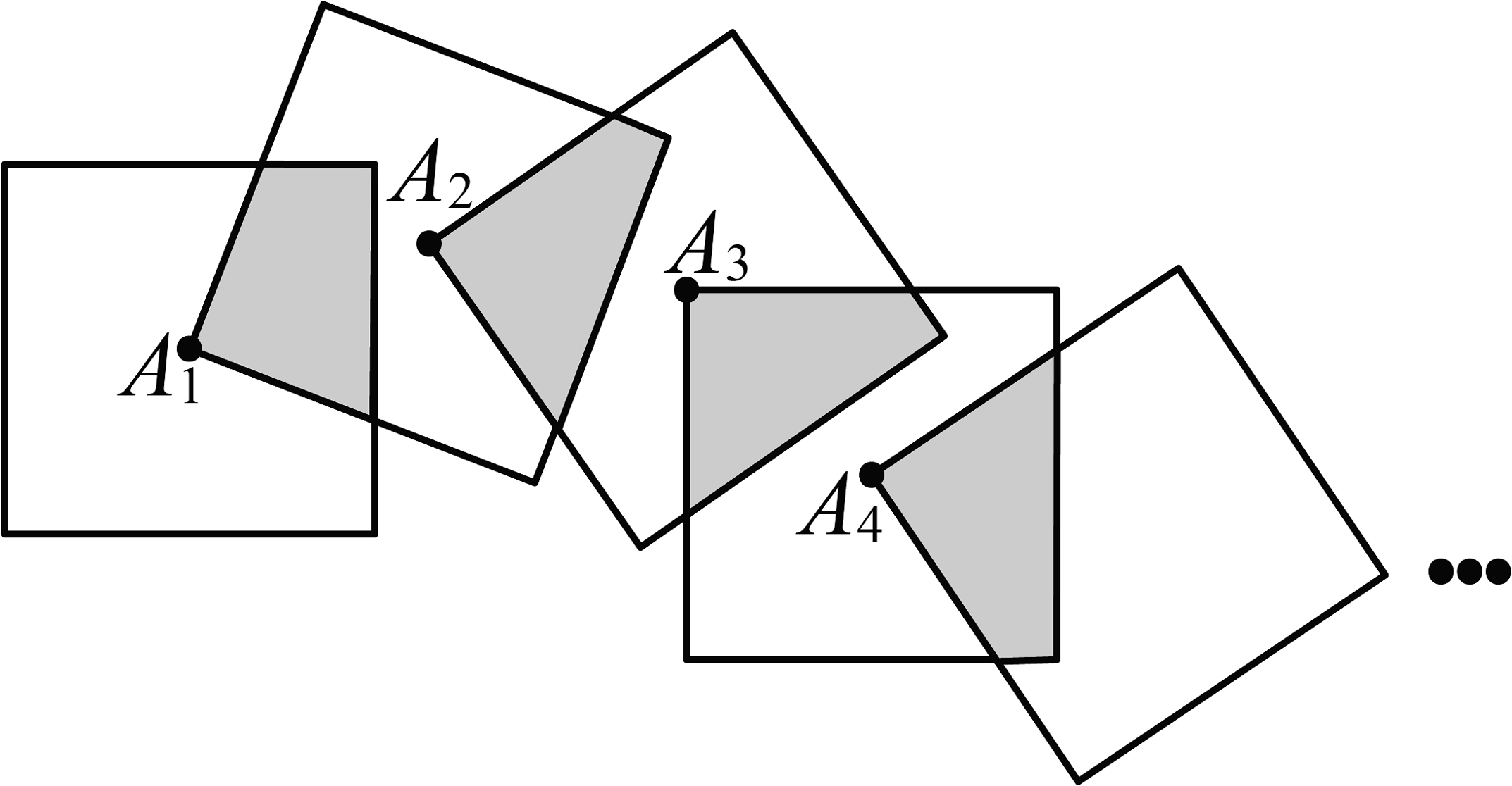 A、 B、 C、 D、
A、 B、 C、 D、 -
2、通常情况下,无色酚酞溶液遇酸性溶液(或中性溶液)不变色,遇碱性溶液变为红色,实验室现有四瓶因标签污损无法分辨的无色溶液,实验课上老师让学生用无色酚酞溶液检测其酸碱性,已知这四种溶液分别是盐酸(呈酸性)、白醋(呈酸性)、氢氧化钠溶液(呈碱性)、氢氧化钙溶液(呈碱性)中的一种.小颖同时任选两瓶溶液用无色酚酞溶液进行检测,则溶液恰好都变红色的概率为( )A、 B、 C、 D、
-
3、如图,数轴上有三个点,分别表示数 , , 16,有两条动线段和(点与点重合,点与点重合,且点在点的左边,点在点的左边), , , 线段以每秒1个单位的速度从点开始向右匀速运动,同时线段以每秒3个单位的速度从点开始向右匀速运动.当点运动到点时,线段立即以相同的速度返回;当点回到点时,线段同时停止运动.设运动时间为秒(整个运动过程中,线段和保持长度不变).
 (1)、两线段运动前,点表示的数为______,点表示的数为______.(2)、在整个运动过程中,当时,求出点表示的数.(3)、在整个运动过程中,当两条线段有重合部分时,速度均变为原来的一半,当重合部分消失后,速度恢复,请直接写出当线段和重合部分长度为1时所对应的的值.
(1)、两线段运动前,点表示的数为______,点表示的数为______.(2)、在整个运动过程中,当时,求出点表示的数.(3)、在整个运动过程中,当两条线段有重合部分时,速度均变为原来的一半,当重合部分消失后,速度恢复,请直接写出当线段和重合部分长度为1时所对应的的值. -
4、观察下面三行数:
第一行:①
第二行:0、6、、18、、66、②
第三行:5、、11、、35、、③
探索他们之间的关系,寻求规律解答下列问题:
(1)、直接写出第①行数的第8个数是______;第②行数的第9个数是______;(2)、取第②行的连续三个数,请判断这三个数的和能否为 , 并说明理由;(3)、取每一行的第个数,从上到下依次记作 , 若对于任意的正整数均有为一个定值,求的值及这个定值. -
5、小芳房间窗户如图所示,其中上方的装饰物由两个四分之一圆和一个半圆组成(它们的半径相同),已知长方形窗户的长为 , 宽为 .
 (1)、装饰物所占的面积是多少?(结果用表示,要求化简).(2)、窗户中能射进阳光的面积是多少?(窗框面积忽略不计)
(1)、装饰物所占的面积是多少?(结果用表示,要求化简).(2)、窗户中能射进阳光的面积是多少?(窗框面积忽略不计) -
6、(1)已知 , , 且 , 求的值.
(2)已知和互为相反数 , 和互为倒数,x的绝对值等于2,求式子:的值.
-
7、已知 , 求的值.
-
8、解下列一元一次方程.(1)、(2)、
-
9、计算.(1)、(2)、
-
10、已知:表示不超的最大整数.例如: , . 令关于的等式(是整数).例如: , 则下列结论正确的有(填序号)
①;②;③;④或1
-
11、如图,将9个数填入空格中,使每行、每列以及两条对角线上的3个数之和相等,则的值为 .
2
-
12、若是方程的解,则的值为 .
-
13、若多项式是四次三项式,则的值是 .
-
14、若气温为零上 , 记作 , 则气温为零下 , 记作℃.
-
15、有一数值转换器,原理如图,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2024次输出的结果是( )
 A、8 B、4 C、2 D、1
A、8 B、4 C、2 D、1 -
16、以下等式变形:①若 , 则;②若 , 则;③若 , 则;④若 , 则 . 其中正确的有( )个A、1 B、2 C、3 D、4
-
17、若 , 则代数式的值为( )A、2016 B、2020 C、2022 D、2024
-
18、下列结论正确的是( )A、 B、若 , 则 C、(精确到) D、近似数万是精确到千位
-
19、某数学兴趣小组在探究函数y=x2﹣2|x|+3的图象和性质时,经历了以下探究过程:
 (1)、研究函数特点:
(1)、研究函数特点:该小组认为,可以将该函数转化为已经学过的二次函数来研究,即将绝对值符号去掉,得到分段函数(每段均为二次函数),其解析式为(填空):y=x2﹣2|x|+3 .
(2)、画图象:在给出的坐标系中,分别画出当x≥0时和x<0时所对应的二次函数的图象;(要求描出横坐标分别为﹣3,﹣2,﹣1,0,1,2,3所对应的点)
(3)、研究性质:根据函数图象,完成以下问题:
①观察函数y=x2﹣2|x|+3的图象,以下说法正确的有 (填写正确选项的代码).
A.对称轴是直线x=1
B.函数y=x2﹣2|x|+3的图象有两个最低点,其坐标分别是(﹣1,2)、(1,2)
C.当﹣1<x<1时,y随x的增大而增大
D.当函数y=x2﹣2|x|+3的图象向下平移3个单位长度时,图象与x轴有三个公共点.
②结合图象探究发现,当m满足 时,方程x2﹣2|x|+3=m有四个解;
③设函数y=x2﹣2|x|+3的图象与其对称轴相交于P点,当直线y=n和函数y=x2﹣2|x|+3图象只有两个交点时,且这两个交点与点P所构成的三角形是等腰直角三角形,则n的值为 .
-
20、已知二次函数 .(1)、求二次函数图象的顶点坐标;(2)、当时,函数的最大值和最小值分别为多少?(3)、若点 , 均在该抛物线上,且 , 求点横坐标的取值范围.