相关试卷

1、如图， $△ A B C$ 是边长为6的等边三角形， $P$ 是 $A C$ 边上一动点，由点 $A$ 向点 $C$ 运动（与 $A$ ， $C$ 不重合）， $Q$ 是 $C B$ 延长线上一点，与点 $P$ 同时以相同的速度由点 $B$ 向 $C B$ 延长线方向运动（点 $Q$ 不与点 $B$ 重合），过点 $P$ 作 $P E ⊥ A B$ 于点 $E$ ，连接 $P Q$ 交 $A B$ 于点 $D$ ．

(1)、若设 $A P = x$ ，则 $P C =$ ______， $Q C =$ ______；（用含 $x$ 的式子表示）

(2)、 $∠ B Q D = 30 °$ 时，求 $A P$ 的长；

(3)、在运动过程中，线段 $D E$ 的长是否发生变化？如果不变，求出线段 $D E$ 的长；如果变化，请说明理由．

查看解析
2、某轮船由西向东航行，在A处测得小岛 $P$ 的方位是北偏东 $75 °$ ，又继续航行16海里后，在 $B$ 处测得小岛 $P$ 的方位是北偏东 $60 °$ ，求：

(1)、此时轮船与小岛 $P$ 的距离 $B P$ 是多少海里？

(2)、小岛 $P$ 方圆7.5海里内有暗礁，如果轮船继续向东行驶，请问轮船有没有触礁的危险？请说明理由．

查看解析
3、如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 12$ ．

(1)、请用无刻度的直尺和圆规作出 $∠ C A B$ 的平分线（保留作图痕迹，不写作法）；

(2)、若（1）中所作的角平分线与边 $B C$ 交于点 $D$ ，过点 $D$ 作 $D E ⊥ A B$ 于点 $E$ ．若 $C D = 4$ ， $S_{△ A B D} = 30$ ，求 $B E$ 的长．

查看解析
4、如图， $△ A B C$ 三个顶点的坐标分别为 $A (- 4, 1)$ ， $B (- 3, 3)$ ， $C (- 1, 2)$ ．

(1)、作出 $△ A B C$ 关于 $y$ 轴对称的 $△ A^{'} B^{'} C^{'}$ ，并写出 $A^{'} 、 B^{'} 、 C^{'}$ 三个点的坐标；

(2)、在 $x$ 轴上画出点 $P$ ，使 $P A + P C$ 最小，并写出点 $P$ 的坐标．（不写作法，保留作图痕迹）

查看解析
5、如图，在直线 $A C$ 的同一侧作两个等边 $△ A B D$ 和 $△ B C E$ ，连接 $A E$ 与 $C D$ 交于点 $H$ ， $A E$ 与 $D B$ 交于点 $G$ ， $B E$ 与 $C D$ 交于点 $F$ ，下列结论：① $A E = D C$ ；② $∠ A H D = 60 °$ ；③ $△ B G F$ 是等边三角形；④ $D G = B G$ ；⑤ $B H$ 平分 $∠ G H F$ ．其中正确的结论有．

查看解析
6、如图， $O P$ 平分 $∠ A O B$ ， $∠ A O P = 15 °$ ， $P C ∥ O A$ ， $P D ⊥ O A$ ，若 $P D = 1$ ，则 $P C =$ ．

查看解析
7、如图， $∠ A O B$ 内一点 $P$ ， $P_{1}$ ， $P_{2}$ 分别是 $P$ 关于 $O A$ 、 $O B$ 的对称点， $P_{1} P_{2}$ 交 $O A$ 于点 $M$ ，交 $O B$ 于点 $N$ ．若 $△ P M N$ 的周长是 $3 cm$ ，则 $P_{1} P_{2}$ 的长为．

查看解析
8、如图，将边长相等的一个正方形和一个正五边形叠放在一起，则 $∠ 1 =$ ．

查看解析
9、在平面直角坐标系中，点 $A (3, 1 - m)$ 与点 $B (n - 1, 1)$ 关于 $x$ 轴对称，则 $m + n$ 的值为．

查看解析
10、如图，在一个池塘两旁有一条笔直小路（ $B$ ， $C$ 为小路端点）和一棵小树（ $A$ 为小树位置）．测得的相关数据为： $∠ A B C = 60 °$ ， $∠ A C B = 60 °$ ， $B C = 15$ 米，则 $A C =$ 米．

查看解析
11、如图，等腰 $Rt △ A B C$ 中， $A B = A C, ∠ B A C = 90 °, A D ⊥ B C$ 于点D， $∠ A B C$ 的平分线分别交 $A C 、 A D$ 于E、F两点，M为 $E F$ 的中点， $A M$ 的延长线交 $B C$ 于点N，连接 $D M$ ，下列结论：① $D F = D N$ ；② $△ A F E$ 为等腰三角形；③ $∠ N A C = 22.5 °$ ；④ $A E = N C$ ，其中正确结论有（）

A、1个 B、2个 C、3个 D、4个

查看解析
12、小丽与爸妈在公园里荡秋千．如图，小丽坐在秋千的起始位置A处， $O A$ 与地面垂直，两脚在地面上用力一蹬，妈妈在距地面 $0.8 m$ 高的B处接住她后用力一推，爸爸在C处接住她．若妈妈与爸爸到 $O A$ 的水平距离 $B D 、 C E$ 分别为 $1.2 m$ 和 $1.6 m$ ， $∠ B O C = 90 °$ ．爸爸在C处接住小丽时，小丽距离地面的高度是（）

A、 $1 m$ B、 $1.2 m$ C、 $1.4 m$ D、 $1.6 m$

查看解析
13、如图，一副三角板叠放在一起， $∠ A = 90^{\circ}$ ， $∠ C = 30^{\circ}$ ， $∠ D = 45^{\circ}$ ，则 $α$ 的度数为（）

A、 $175^{\circ}$ B、 $165^{\circ}$ C、 $155^{\circ}$ D、 $150^{\circ}$

查看解析
14、若一个等腰三角形的两边长分别为4，8，则第三边的长为（）

A、4 B、6 C、8 D、4或8

查看解析
15、下列图形中不是轴对称图形的个数是（）

A、4 B、3 C、2 D、1

查看解析
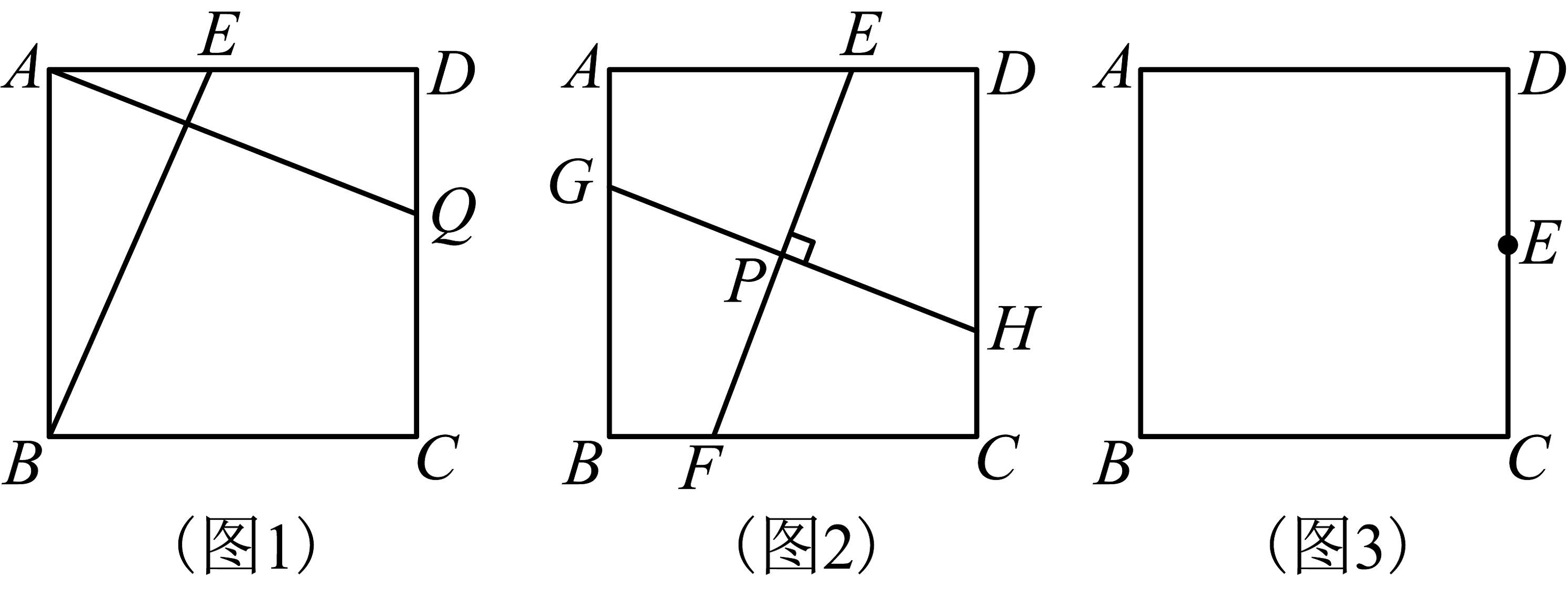
16、在习题课上，老师让同学们以课本一道习题“如图1，A，B，C，D四家工厂分别坐落在正方形城镇的四个角上．仓库E和Q分别位于AD和DC上，且ED＝QC．证明两条直路BE＝AQ且BE⊥AQ．”为背景开展数学探究．
(1)独立思考：将上题条件中的ED＝QC去掉，将结论中的BE⊥AQ变为条件，其他条件不变，那么BE＝AQ还成立吗？请写出答案并说明理由；
(2)合作交流：“祖冲之”小组的同学受此问题的启发提出：如图2，在正方形ABCD内有一点P，过点P作EF⊥GH，点E、F分别在正方形的对边AD、BC上，点G、H分别在正方形的对边AB、CD上，那么EF与GH相等吗？并说明理由．
(3)拓展应用：“杨辉”小组的同学受“祖冲之”小组的启发，想到了利用图2的结论解决以下问题：
如图3，将边长为10cm的正方形纸片ABCD折叠，使点A落在DC的中点E处，折痕为MN，点N在BC边上，点M在AD边上．请你画出折痕，则折痕MN的长是　　；线段DM的长是　　．

查看解析
17、已知某平台在售的故宫文创产品书灯有A，B两个系列，A系列产品比B系列产品的售价低50元，1000元购买A系列产品的数量与1500元购买B系列产品的数量相等．按定价销售一段时间后发现：B系列产品按定价销售，每天可以卖500件，若B系列产品每降1元，则每天可以多卖10件．

(1)、A系列产品和B系列产品的售价各是多少？

(2)、为了使B系列产品每天的销售额为96000元，而且尽可能让顾客得到实惠，求B系列产品的实际售价应定为多少元/件？

查看解析
18、如图，在四边形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点O，点M，P，N，Q分别在 $O A$ ， $O B$ ， $O C$ ， $O D$ 上，连接而成的四边形 $M P N Q$ 是矩形，且 $A M = B P = C N = D Q$ ，求证：四边形 $A B C D$ 是矩形．

查看解析
19、如图，一个可以自由转动的转盘被分成4个相同的扇形，这些扇形内分别标有数字2，5，5，3，指针的位置固定．转动转盘，当转盘自动停止后，指针指向一个扇形的内部，则该扇形内的数字即为转出的数字，计为转动转盘一次（若指针指向两个扇形的分割线，则不计转动的次数，重新转动转盘，直到指针指向一个扇形的内部为止）．

(1)、转动转盘一次，转出的数字为2的概率是______；

(2)、转动转盘两次，请利用画树状图或列表的方法，求这两次转出的数字之和是5的倍数的概率．

查看解析
20、如图，在荾形 $A B C D$ 中，过点B作 $B E ⊥ A D$ 于点 $E$ ，过点 $B$ 作 $B F ⊥ C D$ 于点 $F$ ，求证： $D E = D F$ ．

查看解析

上一页 849 850 851 852 853 下一页跳转