-
1、 如图，已知 AC 是⊙O 的直径，AB=6，BC=8，D 是弧BC 的中点，连结OD，交 BC于点E，则 DE= ( )
A、1 B、2 C、3 D、4 -
2、如图，点 P 是△ABC的重心，过点 P 作AC 的平行线，分别交 AB，BC于点 D，E.若AC=6，则DE的长为( )
A、2 B、3 C、4 D、5 -
3、
(1)、如图①，已知 OC 是∠AOB 的平分线，P是OC上任意一点，点D，E分别在边 OA，OB 上，连 结 PD，PE，∠AOB +∠DPE=180°.若∠AOB=60°，OD+OE= ， 则OP的长为；(2)、如图②，在▱ABCD 中，∠ABC=60°，BE平分∠ABC交AD 于点E，连结CE，将CE 绕点 E 旋转，当点 C 的对应点 F 落在边AB 上时，若 求四边形BCEF的面积. -
4、 在△ABC中，AB=AC，∠BAC=90°，BD平分∠ABC交AC于点 D.
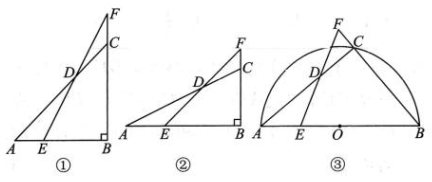
(1)、如图①，F 为 BC 上一点，连结 AF交BD于点E.若AB=BF，求证：BD垂直平分AF；(2)、如图②，CE⊥BD，垂足 E 在 BD 的延长线上，试判断线段CE，BD 之间的数量关系，并说明理由；(3)、如图③，F 为 BC 上一点，∠EFC= ∠ABC，CE⊥EF，垂足为E，EF与AC 交于点M.直接写出线段CE，FM之间的数量关系. -
5、如图，以等腰三角形ABC 的底边 BC为直径作⊙O，分别交 AB，AC边于点 D，E，过点 E 作 EF⊥BC于点 F，∠CEF的平分线交 BC于点 G.若 BD=3，CG=1，则 FG= ， AE=.
(参考素材：角平分线定理：三角形一个角的平分线分对边所成的两条线段与这个角的两边对应成比例，如
-
6、如图，在四边形 ABCD中，AC平分∠BAD，BC=CD=2，AB=5，AD=3，则 AC的长为.
-
7、 如图，半圆 O 的直径AB=5，AC，AD为弦.若 AC=3，AD 平分∠BAC，则AD=.
-
8、 如图，四边形 ABCD为平行四边形，∠BAD的平分线AF交CD 于点E，交 BC的延长线于点 F，连结 BE.若 BE⊥AF，EF= ， 则AB的长为.
-
9、如图，在等边三角形ABC中，点 D，E 分别在边 AC，BC上，连结DE，∠ADE的平分线过△ABC的内心O，交AB 于点 F，连结 EF.若要知道△ABC的周长，则只需要知道下列哪个三角形的周长?该三角形是 ( )
A、△CDE B、△ADF C、△BEF D、△DEF -
10、如图，AE，BE，CE分别平分∠BAC，∠ABC，∠ACB，ED⊥BC于点D，ED=3，△ABC的面积为 36，则△ABC的周长为 ( )
A、48 B、36 C、24 D、12 -
11、如图，在△ABC中，AD平分∠BAC，E 是BC的中点，BD⊥AD 于点D.若AC=7，AB=4，则DE的长为 ( )
A、1 B、2 C、 D、 -
12、如图，DE 是△ABC的中 位线，∠ACB 的平分线交 DE 于点 F，AC=12，BC=18，则DF的长为 ( )
A、9 B、6 C、3 D、2 -
13、 【阅读材料】
问题
如图，AB，CD 相交于点O，O 是 AB 的中点，AC∥BD，求证：O是CD 的中点.
问题分析
由条件易证△AOC≌△BOD，从而得到OC=OD，即O是CD 的中点.
方法提取
构造“平行8字形”全等三角形模型是证明线段相等的一种常用方法.
请运用上述阅读材料中获取的经验和方法解决下列问题.
【基础应用】
已知在△ABC中，. 点 E 在边 AB 上，点F 在边 BC的延长线上，连结EF交AC 于点 D.
(1)、如图①，若AB=BC，AE=CF，求证：D是EF的中点；(2)、如图②，若AB=2BC，AE=2CF，探究CD 与 BE 之间的数量关系；(3)、【灵活应用】如图③，AB是半圆O的直径，C是半圆上一点，E 是AB 上一点，点 F 在 BC 的延长线上， 当点C从点B运动到点A，点D运动的路径长为 ， CF 扫过的面积为.
-
14、【问题呈现】小明在数学兴趣小组活动时遇到一个几何问题：如图①，在等边三角形ABC中，AB=3，点M，N分别在边 AC，BC上，且 AM=CN，试探究线段MN长度的最小值.
【问题分析】小明通过构造平行四边形，将双动点问题转化为单动点问题，再通过定角发现这个动点的运动路径，进而解决上述几何问题.
【问题解决】如图②，过点C，M分别作MN，BC的平行线，并交于点 P，作射线 AP.
在【问题呈现】的条件下，回答下列问题：
(1)、求证：AM=MP；(2)、∠CAP 的大小为度，线段 MN长度的最小值为.(3)、【方法应用】某种简易房屋在整体运输前需用钢丝绳进行加固处理，如图③.小明收集了该房屋的相关数据，并画出了示意图，如图④，△ABC是等腰三角形，四边形 BCDE 是矩形，AB=AC=CD=2米，∠ACB=30°.MN是一条两端点位置和长度均可调节的钢丝绳，点 M在AC 上，点 N 在 DE 上.在调整钢丝绳端点位置时，其长度也随之改变，但需始终保持AM=DN.钢丝绳 MN长度的最小值为米. -
15、小明在求代数式 的最小值时，采用如下方法：如图，在平面直角坐标系中，设M(x，0)为x轴上的一个动点，选取点 A(0，1)和B(4，2)，根据两点之间的距离公式，得 通过构造，将求代数式的最小值转化为求AM+BM的最小值.由此小明求出 的最小值为.
-
16、如图，在 Rt△ABC 中，∠ACB=90°，AB=2，若 D 为直线 AC左侧一点，当△ABC∽△CAD时，BC+CD的最大值为 ( )
A、 B、 C、 D、 -
17、对于一元二次方程，我国古代数学家还研究过其几何解法.以方程x(x+6)=72为例加以说明.数学家赵爽在其所著的《勾股圆方图注》中记载的方法是：如图，将四个长为x+6，宽为x的矩形纸片拼成一个大正方形，则大正方形的边长是x+6+x，面积是四个矩形的面积与中间小正方形的面积之和，即 据此易得 小明用此方法解关于x的方程x(3x-n)=24，其中3x-n>x构造出同样的图形，已知小正方形的面积为4，则n的值为 ( )
A、2 B、4 C、6 D、8 -
18、在每个小正方形的边长均为1的网格图形中，每个小正方形的顶点称为格点.如图，在6×6的正方形网格图形ABCD中，M，N分别是AB，BC上的格点，BM=4，BN=2.若P是这个网格图形中的格点，连结PM，PN， 则 所 有 满 足 ∠MPN = 45°的△PMN中，边 PM的长的最大值是 ( )
A、4 B、6 C、 D、3 -
19、老师布置的作业中有这样一道题：
甲同学认为AB，AC，AD这三条线段不在同一个三角形中，无法解答，老师给的题目有错误；乙同学认为可以从中点D出发，构造辅助线，利用全等的知识解决；丙同学认为没必要借助全等三角形的知识，只需取 AB 的中点构造三角形的中位线，就可以解决.关于三位同学的思考过程，你认为正确的是 ( )
A、甲 B、乙 C、丙 D、乙和丙 -
20、转化是解决数学问题常用的思想方法之一，它可以在数与数、数与形、形与形之间灵活应用.请解答下面的问题.
如图①， 在 △AOB 中， OA = OB，∠AOB=90°.
(1)、【基础巩固】将图①中△AOB绕点 B 按顺时针方向旋转60°得到△DCB，如图②，连结 OC，求证：OC=OB.
(2)、【思考探究】将图①中△AOB 绕点 B 按顺时针方向旋转60°并缩小得到△DCB，如图③，使 ， 连结OC，AD.
①求证：△OBC∽△ABD；
②用等式表示 AD 与AB 之间的数量关系，并说明理由.
(3)、【拓展延伸】将图①中△AOB绕点 B 按顺时针方向旋转某个角度(小于 180°)并缩小得到△DCB，如图④，使 连 结 OC，AC，AD.当OC=OB时，求 的值.