相关试卷

1、如图，在矩形AB-CD中， $A D = 3 A B = 3 \sqrt{10} ，$ P 是 AD 的中点，点 E 在 BC上，CE=2BE，点 M，N 在线段BD上.若△PMN是等腰三角形，且底角与∠DEC 相等，则MN的长为( )

A、6或2 B、3或 $\frac{15}{8}$ C、2 或3 D、6 或 $\frac{15}{8}$

查看解析
2、已知二次函数y=a(x+m-4)(x-m)(a≠0，a，m是常数)的图象上有两点A(x₁ ， y₁)，B(x₂ ， y₂)(其中 $x_{1} < x_{2}) ，$ 则下列说法正确的是( )

A、若 $a > 0 ， x_{1} + x_{2} < 5 ，$ 则 $a (y_{1} - y_{2}) < 0$ B、若 $a > 0 ， x_{1} + x_{2} < 3 ，$ 则 $a (y_{1} - y_{2}) > 0$ C、若 $a < 0 ， x_{1} + x_{2} > 3 ，$ 则 $a (y_{1} - y_{2}) < 0$ D、若 $a < 0 ， x_{1} + x_{2} > 5 ，$ 则 $a (y_{1} - y_{2}) > 0$

查看解析
3、在△ABC中，AB=AC，AB的垂直平分线与AC 所在的直线相交所得的锐角为 40°，则∠B 的度数为( )

A、20°或70° B、30°或60° C、25°或65° D、35°或65°

查看解析
4、在△ABC中，AB=13，AC=15，AD⊥BC于点D，且AD=12，则BC的长为 ( )

A、14 B、4 C、14或4 D、14 或9

查看解析
5、点A，B，C在⊙O上，∠AOB=100°，点 C 不与A，B重合，则∠ACB的度数为 ( )

A、50° B、80°或50° C、130° D、50°或130°

查看解析
6、等腰三角形的一个内角是50°，则它的底角的度数是 ( )

A、50° B、50°或65° C、80°或50° D、65°

查看解析
7、 A为数轴上表示-2的点，当点 A 沿数轴移动4个单位长度到点 B时，点B 所表示的数为 ( )

A、2 B、-6 C、2 或-6 D、4

查看解析
8、

(1)、【问题情境建构函数】
如图①，在矩形 ABCD 中，AB=4，M是CD 的中点，AE⊥BM，垂足为 E.设BC=x，AE=y，则y=(用含x的代数式表示).

(2)、【由数想形新知初探】
在上述表达式中，y与x成函数关系，其图象如图②所示.若x 取任意实数，此时的函数图象是否具有对称性?若有，请说明理由，并在图②中补全函数图象.

(3)、【数形结合深度探究】
在“x取任意实数”的条件下，对上述函数继续探究，得出以下结论：①函数值y随x的增大而增大；②函数值 y的取值范围是 $- 4 \sqrt{2} < y < 4 \sqrt{2};$ ③存在一条直线与该函数图象有四个交点；④在图象上存在四点 A，B，C，D，使得四边形 ABCD 是平行四边形.其中正确的是(写出所有正确结论的序号).

(4)、【抽象回归拓展总结】
若将(1)中的“AB=4”改成“AB=2k”，此时y关于x的函数表达式是；一般地，当k≠0，x取任意实数时，类比一次函数、反比例函数、二次函数的研究过程，探究此类函数的相关性质(直接写出3条即可).

查看解析
9、将一副三角尺按如图方式放置在平面直角坐标系中，已知AB=2，反比例函数 $y = \frac{k}{x} (k⟩ 0)$ 的图象恰好经过顶点C，D，DB⊥x轴，则k的值为.

查看解析
10、如图，将面积为7 的正方形 OABC 和面积为9的正方形ODEF 分别绕原点O顺时针旋转，使OA，OD落在数轴上，点 A，D 在数轴上对应的数分别为a，b，则b-a=.

查看解析
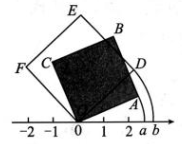
11、如图，在同一平面直角坐标系中，直线l₁：y= $\frac{1}{4} x + \frac{1}{2}$ 与直线 l₂：y=kx+3 相交于点A(2，1)，则方程组 ${\begin{matrix} y = \frac{1}{4} x + \frac{1}{2} ， \\ y = k x + 3 \end{matrix}$ 的解为.

查看解析
12、在平面直角坐标系中，A(a， $2 \sqrt{3}$ )是直线 y= $\sqrt{3} x$ 上一点，以点 A 为圆心，2为半径作⊙A.若P(x，y)是⊙A 上任意一点，则 $\frac{y}{x}$ 的最小值为 ( )

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3} - 1$ D、 $\frac{\sqrt{3}}{3}$

查看解析
13、西周数学家商高总结了用“矩”(如图①)测量物高的方法：把矩的两边放置成如图②的位置，从矩的一端A(人眼)望点 E，使视线通过点 C，记人站立的位置为点 B，量出BG长，即可算得物高EG.令BG=x(m)，EG=y(m).若a=30cm，b=60 cm，AB=1.6m，则y关于x的函数表达式为 ( )

A、 $y = \frac{1}{2} x$ B、 $y = \frac{1}{2} x + 1.6$ C、y=2x+1.6 D、 $y = \frac{1800}{x} + 1.6$

查看解析
14、如图，在平面直角坐标系中，P是以点 $C (- \sqrt{2}, \sqrt{7})$ 为圆心，1为半径的⊙C上的一个动点，已知A(-1，0)，B(1，0)，连结 PA，PB，则 $P A^{2} + P B^{2}$ 的最小值是 ( )

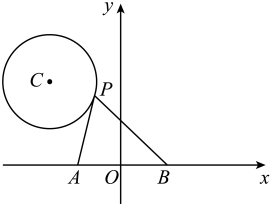A、6 B、8 C、10 D、12

查看解析
15、已知 $t a n α = \frac{1}{2} ， t a n β = \frac{1}{3} ，$ 求α+β的度数.小明经过思考后，画出如图所示的网格并把α和β画在网格中，连结 AD 得到△ABD，且AB=AD，∠DAB=90°.由此可知，α+β=45°.小明这种求解方法体现的数学思想是 ( )

A、数形结合思想 B、分类思想 C、统计思想 D、方程思想

查看解析
16、数学活动课上，小云和小王在讨论涂老师出示的一道代数式求值问题：
已知 $p + q + 2 r = 1 ， p^{2} + q^{2} - 8 r^{2} + 6 r - 5 = 0$ ，求代数式 pq-qr- rp的值.
通过你的运算，代数式 pq-qr-rp的值为

查看解析
17、若 $x^{2} + x y + y = 14$ ， $y^{2} + x y + x = 28 ，$ 则x+y的值为.

查看解析
18、阅读材料：整体代入求值是数学中常用的方法.例如“已知3a-b=2，求代数式6a-2b-1的值.”可以这样解：6a-2b-1=2(3a-b)-1=2×2-1=3.根据阅读材料，解决问题：若x=2是关于x的一元一次方程 ax+b=3的解，则代数式 $4 a^{2} + 4 a b + b^{2} + 4 a + 2 b - 1$ 的值是.

查看解析
19、若x+2y-3=0，则3^x·9^y=.

查看解析
20、我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形，如图所示，已知∠A=90°，BD=4，CF=6，设正方形ADOF的边长为x，则 $x^{2} + 10 x =$ ( )

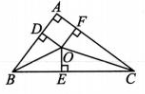A、12 B、16 C、20 D、24

查看解析

上一页 1188 1189 1190 1191 1192 下一页跳转