-
1、如图,在中, , , F为延长线上一点,点在上,且 .
 (1)、求证:;(2)、若 , 求的度数.
(1)、求证:;(2)、若 , 求的度数. -
2、如图,在与中,点C在线段上,且 , , , . 求证: .

-
3、化简: .
-
4、计算: .
-
5、小明在做作业的时候,不小心把墨水滴到了作业本上的等式处,阴影部分即为被墨汁遮住的部分,那么被墨汁遮住的代数式是 .
-
6、如图,中, , , 平分 , 则 .
-
7、如图,AD=BC,要得到△ABD和△CDB全等,可以添加的条件是 .

-
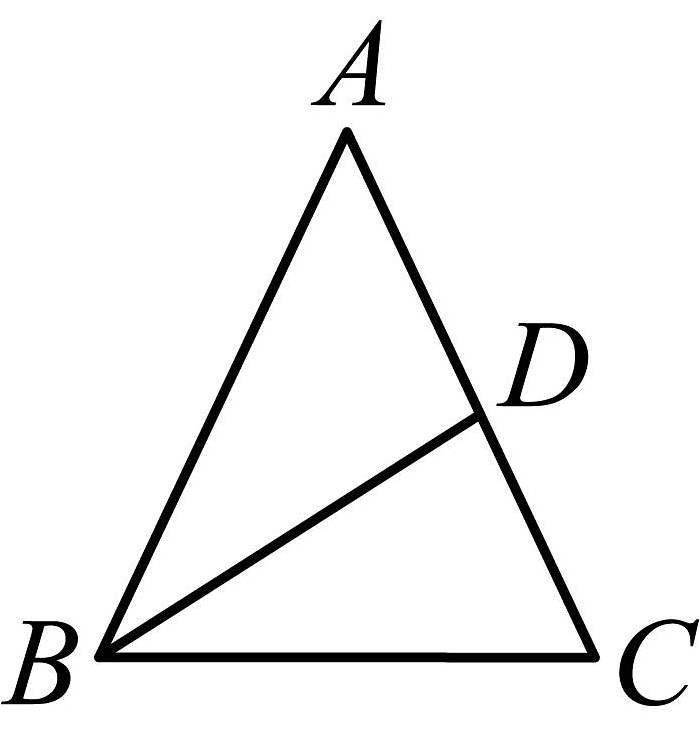
8、如图,在中,按下列步骤作图:①分别以B、C为圆心,以大于的长为半径作弧,两弧相交于两点M、N;②作直线交于点D,连接 . 若 , , 则的周长为( )
 A、7 B、9 C、11 D、13
A、7 B、9 C、11 D、13 -
9、如图,与都是等边三角形, , 若不动,将绕点C旋转,则在旋转过程中,与的大小关系是( )
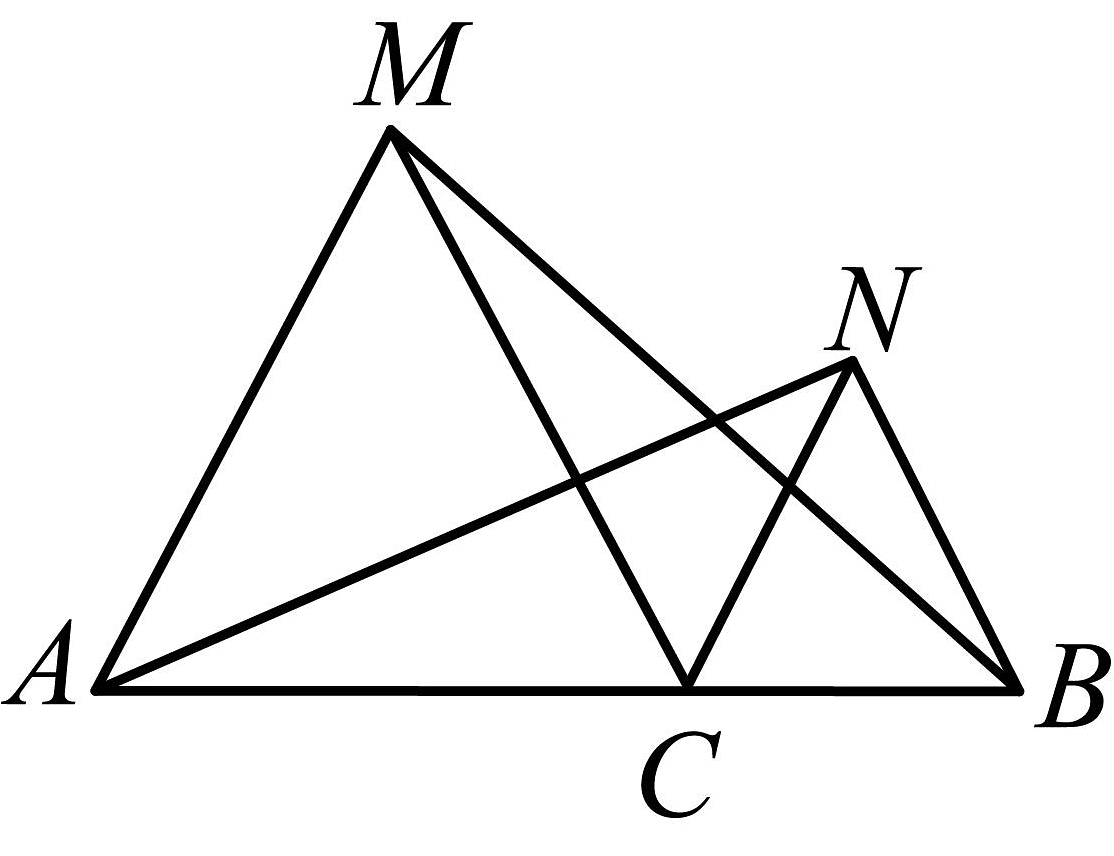 A、 B、 C、 D、无法确定
A、 B、 C、 D、无法确定 -
10、如图,要测量池塘两岸相对的两点A、B间的距离,作线段与相交于点O,使 , , 只要测得C、D之间的距离,就可知道A、B间的距离,此方案依据的数学定理或基本事实是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、如图,在中,分别平分和 , 且相交于点O,若 , 则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12、如图,数轴上点表示的数为 , 点表示的数为 . 点从点出发,以每秒个单位长度的速度沿数轴正方向运动,点出发的同时点从点出发,以每秒个单位长度的速度沿数轴正方向运动,设、两点运动的时间为秒 .
 (1)、点表示的数为________,点表示的数为________.(用含的代数式表示)(2)、当 , 时,分别求线段的长.(3)、当时,求所有符合条件的的值.(4)、若点一直沿数轴的正方向运动,点运动到点时,立即改变运动方向,以原速度沿数轴的负方向运动,到达点时,随即停止运动,在点的整个运动过程中,当时,直接写出的值.
(1)、点表示的数为________,点表示的数为________.(用含的代数式表示)(2)、当 , 时,分别求线段的长.(3)、当时,求所有符合条件的的值.(4)、若点一直沿数轴的正方向运动,点运动到点时,立即改变运动方向,以原速度沿数轴的负方向运动,到达点时,随即停止运动,在点的整个运动过程中,当时,直接写出的值. -
13、概念学习:规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如 , 等,类比有理数的乘方,我们把记作 , 读作“2的3次商”,记作 , 读作“的4次商”.一般地,我们把个相除记作 , 读作“的次商”.
初步探究
(1)直接写出结果:_________;
深入思考
我们知道,有理数的减法运算可以转化为加法运算,除法运算能够转化为乘法运算,那么有理数的除方运算如何转化为乘方运算呢?例: .
(2)试一试:仿照上面的算式,将下列运算结果直接写成乘方(幂)的形式:
_________;_________;
(3)计算: .
-
14、国庆期间七年级(1)班组织同学及家长去动物园游玩,动物园的成人票50元/张,学生票25元/张.国庆期间购票有如下两种优惠方式:
第一种:购买一张成人票赠送一张学生票;
第二种:按购买金额打八折付款.
七年级(1)班共有学生30人,陪同家长x(x不超过30)人.
(1)、用含x的代数式分别表示两种购买方式应支付的金额;(2)、若陪同家长共8人,则七年级(1)班应该选择哪种优惠方式才更省钱? -
15、有这样一道题:“求的值,其中 , ”.小明同学把“”错抄成了“”,但他的计算结果竟然正确,请你说明原因,并计算出正确结果.
-
16、如图是由6个棱长为1的小正方体组成的简单几何体,请在方格纸中分别画出该几何体的主视图、左视图和俯视图.

-
17、计算:
(1)
(2) .
-
18、计算:(1)、(2)、
-
19、如图所示,未来公园的广场背景墙上有一系列用灰砖和白砖铺成的图案,图①有1块灰砖,8块白砖;图②有4块灰砖,12块白砖;以此类推.第个图案中,白色瓷砖的个数为个.

-
20、下面的图形经过折叠可以围成的几何体名称是 .
