-
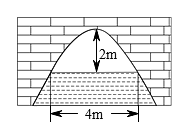
1、如图是抛物线型拱桥,当拱顶离水面时,水面宽 , 当水面宽度为时,水面下降了 .
-
2、下列两个电子数字成中心对称的是 . (填序号)

-
3、如图,二次函数的图象与轴的交点在与之间,对称轴为 , 函数最大值为4,结合图象给出下列结论:①;②;③;④若关于的一元二次方程有两个不相等的实数根,则;⑤当时,随的增大而减小.其中正确的结论有( )
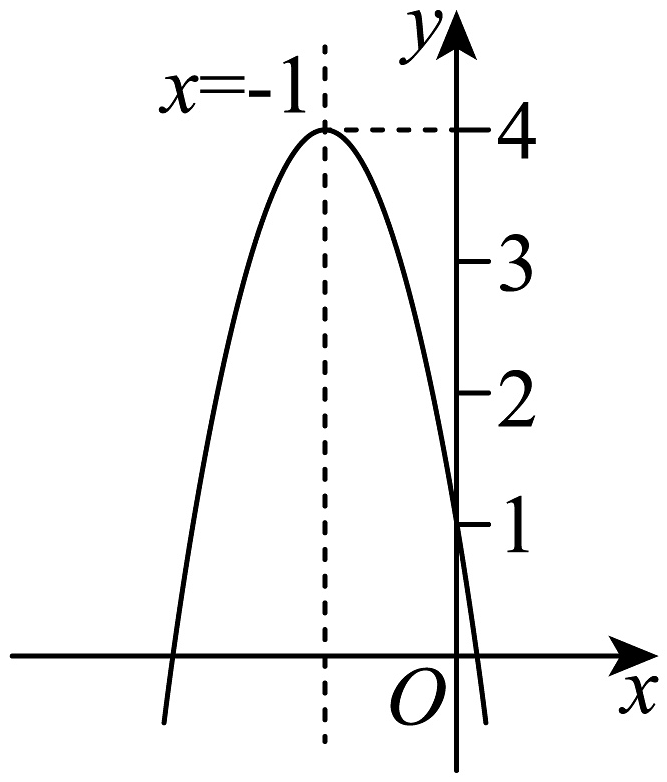 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个 -
4、如图,在中, , , 将绕点逆时针方向旋转得到 , 点恰好落在边上,连接 , 取的中点 , 连接 , 则的长是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、对于二次函数的图象,下列说法正确的是( )A、开口向下 B、对称轴是直线 C、当时,随的增大而减小 D、函数的最大值为4
-
6、一元二次方程的两根为和3,则的值是( )A、-3 B、3 C、-2 D、2
-
7、抛物线的顶点坐标是( )A、 B、 C、 D、
-
8、已知:平面直角坐标系中,点A在y轴的正半轴上,点B在第二象限,AO=AB,BO与x轴正方向的夹角为150°.
(1)试判定△ABO的形状;
(2)如图1,若BC⊥BO,BC=BO,点D为CO的中点,AC、DB交于E,求证:AE=BE+CE;
(3)如图2,若点E为y轴的正半轴上一动点,以BE为边作等边△BEG,延长GA交x轴于点P,问:AP与AO之间有何数量关系,试证明你的结论.

-
9、如图,在四边形中, , , 求证: .

-
10、(1)先化简,再求值: , 其中 .
(2)已知 , 求的值.
(3)已知 , 求下列各式的值:
①;
② .
-
11、如图,已知△ABC,点P为BC上一点.
 (1)、尺规作图:作直线 , 使得点A与点P关于直线对称,直线交直线于 E,交直线于F;(保留作图痕迹,不写作法)(2)、连接 , , 交于点O,若平分 , 请在(1)的基础上说明 .
(1)、尺规作图:作直线 , 使得点A与点P关于直线对称,直线交直线于 E,交直线于F;(保留作图痕迹,不写作法)(2)、连接 , , 交于点O,若平分 , 请在(1)的基础上说明 . -
12、计算:(1)、(2)、(3)、(4)、
-
13、如图,边长为的等边中,是上的中线,且 , 点D在上,连接 , 在的右侧作等边 , 连接 , 则周长的最小值是(用含a,b的式子表示).

-
14、已知 , 则的值是 .
-
15、计算:().
-
16、已知:如图,为的角平分线,且为延长线上的一点, , 过作为垂足,下列结论:①;②;③;④ , 其中正确的结论有( )个
 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1 -
17、计算的结果是( )A、 B、 C、 D、
-
18、如图,中, , , 的垂直平分线交于 , 交于 , , 则( )
 A、8 B、10 C、12 D、15
A、8 B、10 C、12 D、15 -
19、在平面直角坐标系中, , 是抛物线上任意两点,设抛物线的对称轴为直线 .(1)、若 , , 求的值;(2)、求证:当点 , 的坐标是 , 时,;(3)、若对于任意 , 都有 , 求的取值范围.
-
20、如图,四边形内接于 , 是的直径, , 连接 , 过点的直线与的延长线交于点 , 且 .
 (1)、求证:是的切线;(2)、以下与线段 , 线段 , 线段有关的三个结论:① , ② , ③ , 你认为哪个正确?请说明理由.
(1)、求证:是的切线;(2)、以下与线段 , 线段 , 线段有关的三个结论:① , ② , ③ , 你认为哪个正确?请说明理由.