-
1、用反证法证明“若 , 则”时,应假设.
-
2、如图,在等腰直角三角形ACD,∠ACD=90°,AC= , 分别以边AD,AC,CD为直径面半图,所得两个月形图案AGCE和DHCF的面积之和(图中阴影部分)为 .

-
3、下列图形是中心对称图形,但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
4、如图,在矩形中,对角线相交于点 , 且 , 则图中长度为3的线段有( )
 A、2条 B、4条 C、5条 D、6条
A、2条 B、4条 C、5条 D、6条 -
5、已知是完全平方式,则m的值是( )A、1 B、2 C、 D、
-
6、如图,将绕点顺时针旋转得到 . 若点在同一条直线上,则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7、中, , 点 E、F分别是边和上的动点,但始终保持不变.
 (1)、如图①,若求证:(2)、如图②,当与不平行时,(1)中的结论是否依然成立?如果成立,请证明;如果不成立,请说明理由;(3)、设则 周长的最小值为 (用含a 的式子表示).
(1)、如图①,若求证:(2)、如图②,当与不平行时,(1)中的结论是否依然成立?如果成立,请证明;如果不成立,请说明理由;(3)、设则 周长的最小值为 (用含a 的式子表示). -
8、如图①, , 垂足分别为D、E.
 (1)、求证:;(2)、在图①中的边上取一点F,使 , 连接交于点G,连接(如图②).
(1)、求证:;(2)、在图①中的边上取一点F,使 , 连接交于点G,连接(如图②).①求证:;
②若 , 请直接写出的面积.
-
9、如图,在长方形纸片中,四个角是直角,对边平行.点E、F分别在、边上,把长方形纸片沿着折叠,使点C落在点处,点D落在点处.
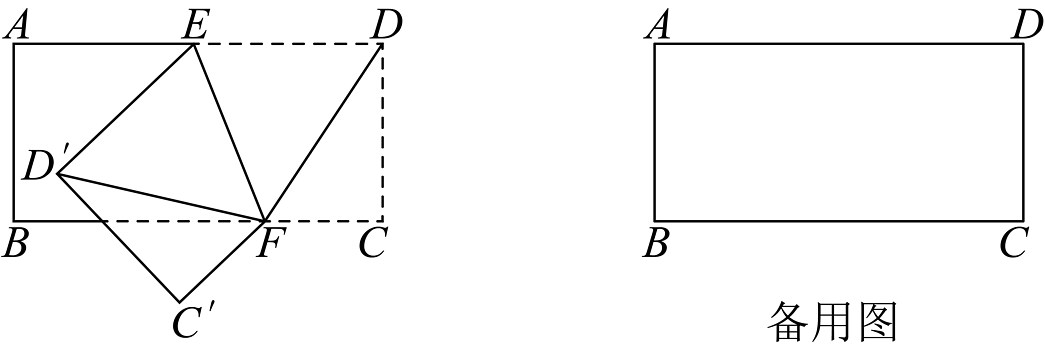 (1)、连接 , , 则 , 依据是 ;(2)、当时,求的度数;(3)、当时,请直接写出的度数(用α表示).
(1)、连接 , , 则 , 依据是 ;(2)、当时,求的度数;(3)、当时,请直接写出的度数(用α表示). -
10、7个如图①的小长方形,长为a,宽为b,按照图②方式不重叠地放在大长方形内,大长方形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为 , 左下角的面积为 的长度为m.
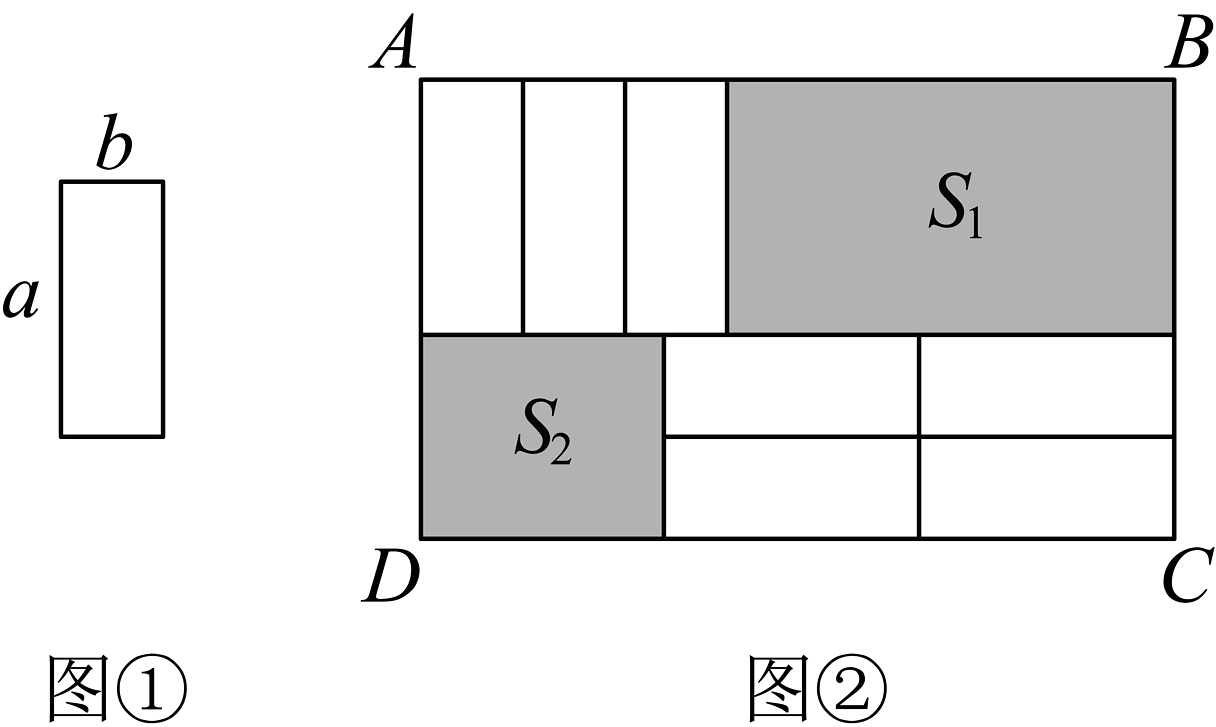 (1)、填空: ____,_______(用含a、b、m的式子表示);(2)、若的值与m的取值无关,求a与b的数量关系;(3)、在(2)的条件下,直接写出的值.
(1)、填空: ____,_______(用含a、b、m的式子表示);(2)、若的值与m的取值无关,求a与b的数量关系;(3)、在(2)的条件下,直接写出的值. -
11、如图,在平面直角坐标系中, 的三个顶点均在正方形网格的格点上.
 (1)、请你画出 关于y轴对称的并写出点 A 的对应点的坐标;(2)、的面积为 ;(3)、请你在y轴上找到一点 P,使得.最小(保留作图痕迹).
(1)、请你画出 关于y轴对称的并写出点 A 的对应点的坐标;(2)、的面积为 ;(3)、请你在y轴上找到一点 P,使得.最小(保留作图痕迹). -
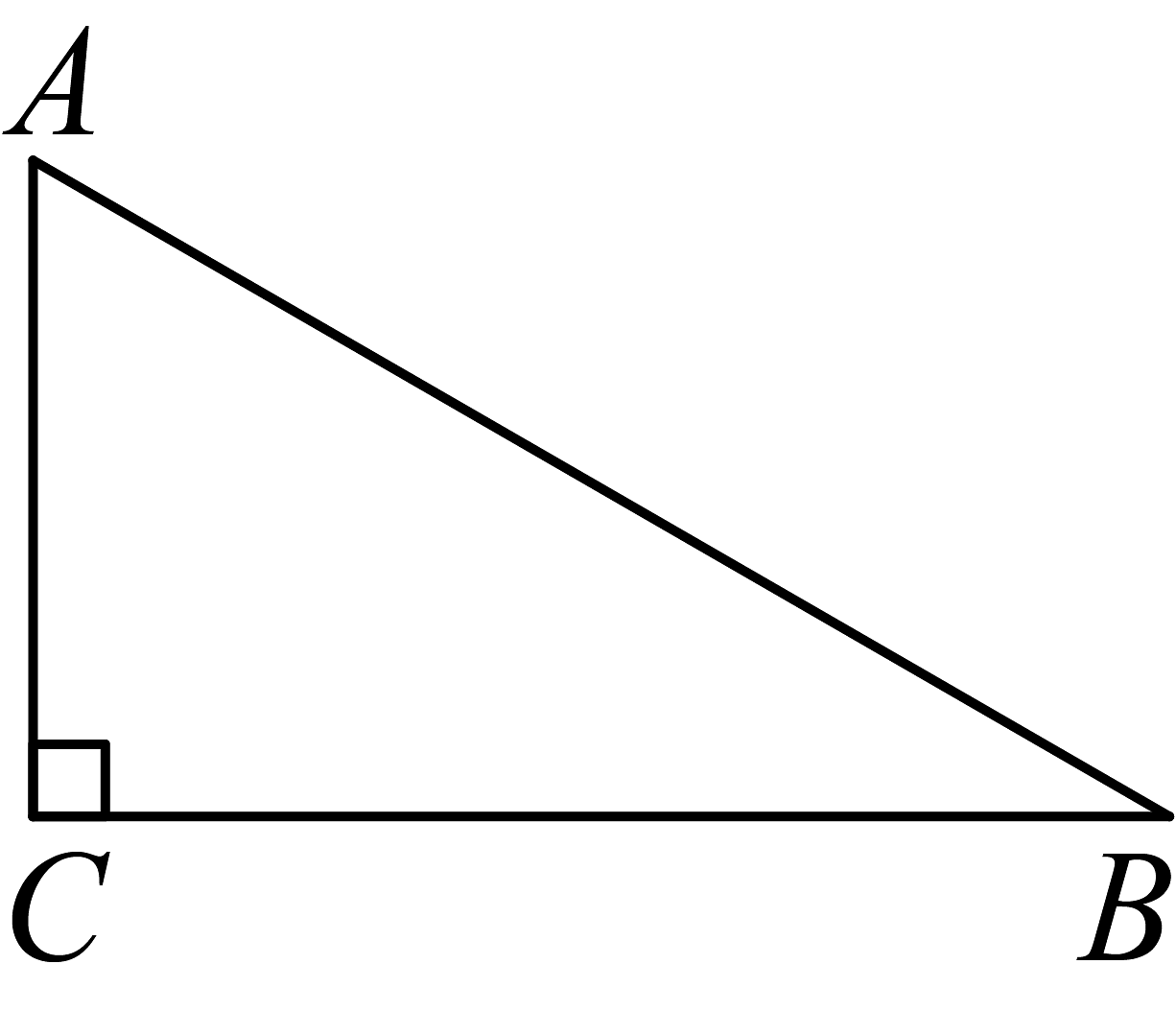
12、如图,要把一块三角形的土地均匀分给甲、乙、丙三家农户去种植.如果∠C=90°,∠B=30°,要使这三家农户所得土地的大小、形状都相同,请你在图中试着分一分,并在图上画出来,并说明你的理由.
-
13、在四边形中,
 (1)、如图①,求证:(2)、如图②,在边上分别取中点M、N,连接 . 若 , 求的度数.
(1)、如图①,求证:(2)、如图②,在边上分别取中点M、N,连接 . 若 , 求的度数. -
14、计算: .
-
15、已知则的值是 .
-
16、若则□内应填的是 .
-
17、在平面直角坐标系中,点关于轴对称的点的坐标是 .
-
18、如图,已知 . 若 , 则∠的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
19、下列运算正确的是( )A、 B、 C、 D、
-
20、若等腰三角形的两边长分别是3和8、则它的第三边的长是( )A、3 B、6 C、8 D、3或8