-
1、如图,与相交于点 , 求证: .

-
2、如图, 三角形纸片中, , 在上取一点 , 以为折痕进行翻折,使的一部分与重合,与延长线上的点重合, 若 , , 则的长度为 .

-
3、如图,已知△ABC的面积是24,D是BC的中点,E是AC的中点,那么△CDE的面积是 .

-
4、已知等腰三角形的一个内角为 , 则另两个角的度数是 .
-
5、如图,和均是等边三角形,A、C、B三点共线,与相交于点P,与分别与 , 交于点M,N.则下列结论:①;②;③;④ . 其中正确的结论有( )
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个 -
6、如图,在中, , , 的垂直平分线交于点 , 交于点 , 则的度数等于( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7、如图, , 点和点是对应顶点,点和点是对应顶点,则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8、正六边形的内角和是( )A、 B、 C、 D、
-
9、如图,和都是等边三角形,且点在一条直线上,连接和 , 交、于点 . 和相交于点 , 连接 .
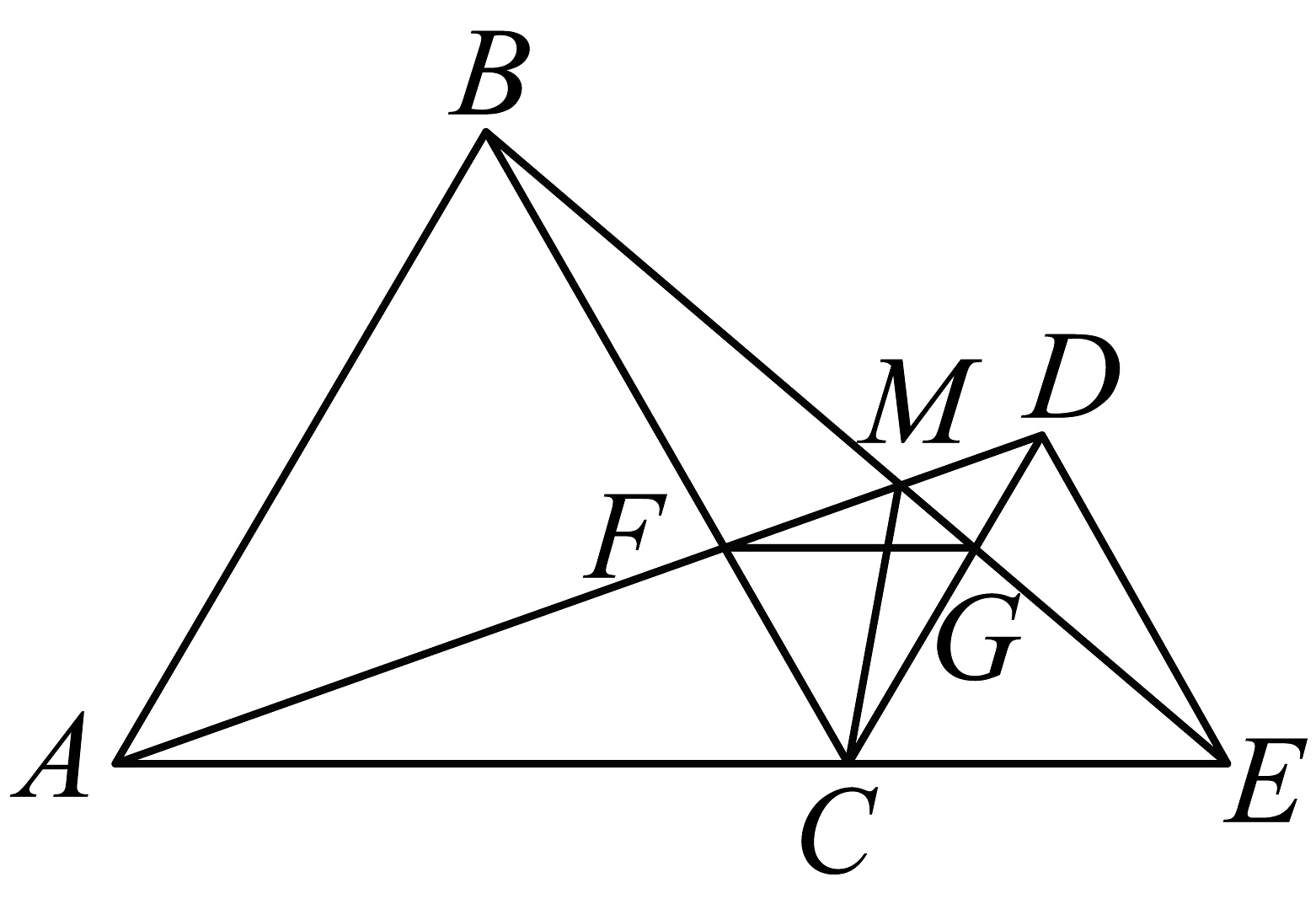 (1)、求证: .(2)、连接 , 请判断的形状,并说明理由.(3)、求证:平分
(1)、求证: .(2)、连接 , 请判断的形状,并说明理由.(3)、求证:平分 -
10、如图,在中, , , 的垂直平分线交于点 , 交于点 , 的垂直平分线交于点 , 交于点 , 连接 , , 求:
 (1)、的度数(2)、的周长
(1)、的度数(2)、的周长 -
11、已知:如图, , , .
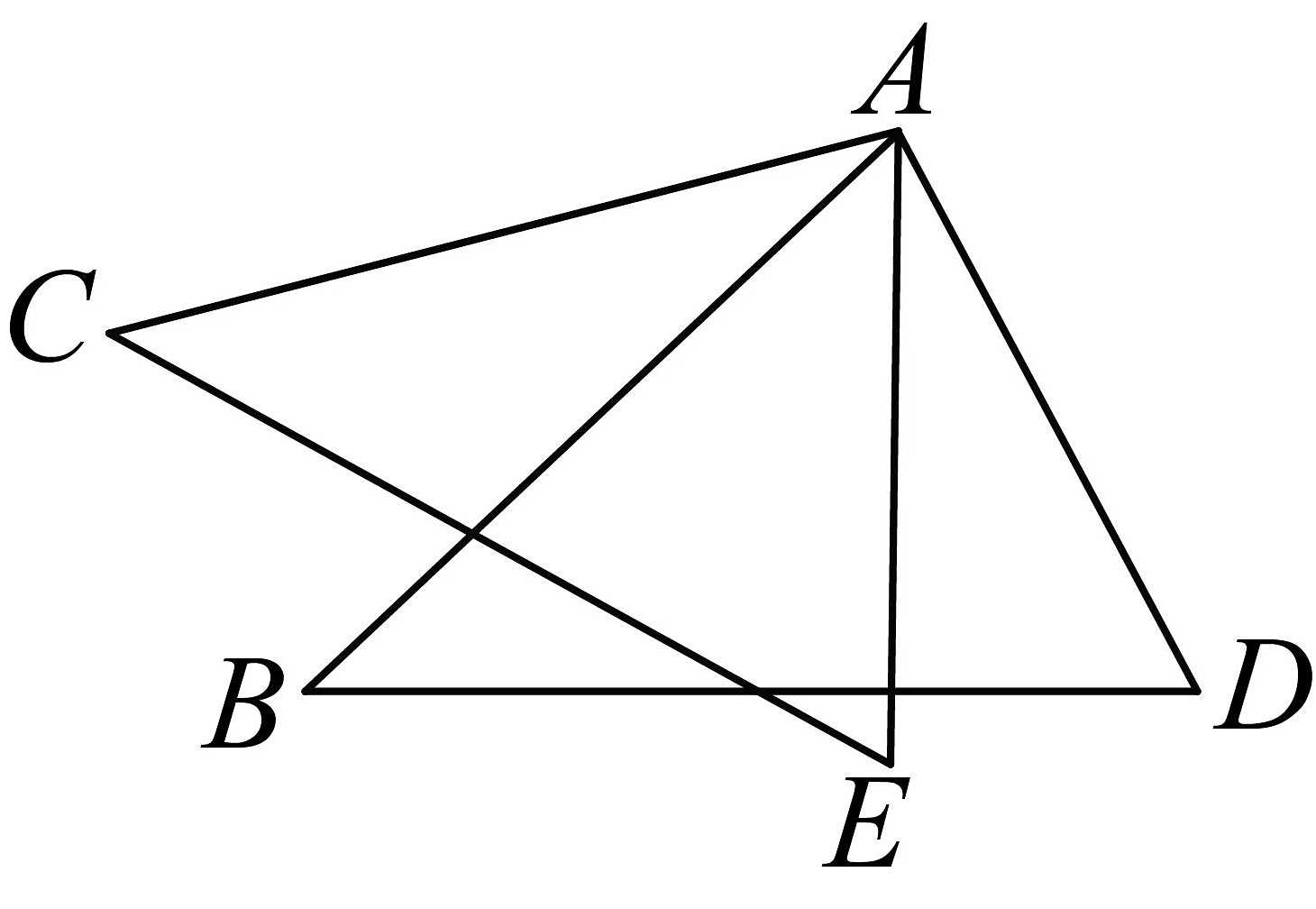
求证: .
-
12、如图,点B、F、C、E在一条直线上, , , . 求证: , .

-
13、若一个多边形内角和与外角和的比为9∶2,则这个多边形的边数是 .
-
14、在中, , 则
-
15、如图, .

-
16、如图,中, , , 垂直平分 , 则的周长是

-
17、如图,△ABC≌△DEC,点B的对应点E在线段AB上,若AB∥CD,∠DCA=40°,则∠B的度数是( )
 A、60° B、65° C、70° D、75°
A、60° B、65° C、70° D、75° -
18、一个多边形的内角和是 , 则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形
-
19、下列交通标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
20、在平面直角坐标系中,任意点到定点的距离等于到直线的距离,记点P的轨迹为抛物线 ,
 (1)、直接写出抛物线的解析式 ;(2)、将抛物线向右平移1个单位长度,再绕点旋转得到抛物线 , 抛物线与x轴交于A,B两点(A左B右),与y轴交于C点,R为抛物线上的动点,如图1,若以A、B、R、C为顶点的四边形为梯形,求点R的坐标;(3)、如图2,过点分别作直线:交(2)中的抛物线于点E,F,直线: ≠0)交抛物线于点G、H,点M、N分别为的中点,若直线与直线平行,求证:为定值,并求出该定值.
(1)、直接写出抛物线的解析式 ;(2)、将抛物线向右平移1个单位长度,再绕点旋转得到抛物线 , 抛物线与x轴交于A,B两点(A左B右),与y轴交于C点,R为抛物线上的动点,如图1,若以A、B、R、C为顶点的四边形为梯形,求点R的坐标;(3)、如图2,过点分别作直线:交(2)中的抛物线于点E,F,直线: ≠0)交抛物线于点G、H,点M、N分别为的中点,若直线与直线平行,求证:为定值,并求出该定值.