相关试卷

1、已知点 $M (1 - a, 2 a + 2)$ ，若点M关于x轴对称点在第四象限，则a的取值范围．

查看解析
2、如图，为了促进当地旅游发展，某地区要修建一个度假村．要使这个度假村到三条公路的距离相等，这个度假村的选址有处可供选择．

查看解析
3、如图，点E、F在 $B C$ 上， $A B = C D$ ， $∠ A F B = ∠ D E C$ ， $A F$ 、 $D E$ 相交于点G，要使得 $△ A B F ≌ △ D C E$ ，则还需添加的条件为．

查看解析
4、已知 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 5$ ， $A C = 4$ ， $B C = 3$ ， $C D ⊥ A B$ 于点D， $∠ C A B$ 的平分线交 $C D$ 于点E，则 $△ A B E$ 的面积为（）

A、 $\frac{8}{3}$ B、3 C、 $\frac{10}{3}$ D、 $\frac{11}{3}$

查看解析
5、如图，已知 $∠ A O B = 35 °$ ，点P是 $∠ A O B$ 内部一点，点M、N分别是 $O A$ 、 $O B$ 上的动点．当 $△ P M N$ 的周长最小时， $∠ M P N$ 的度数为（）

A、 $140 °$ B、 $110 °$ C、 $90 °$ D、 $70 °$

查看解析
6、如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $D E$ 垂直平分 $A B$ ，垂足为D，交 $B C$ 于点E， $A E$ 平分 $∠ B A C$ ，那么下列关系式中不成立的是（）

A、 $∠ B = ∠ C A E$ B、 $∠ D E A = ∠ C E A$ C、 $A C = 2 C E$ D、 $A B = 2 A C$

查看解析
7、如图， $∠ A C B = 90 °$ ， $A C = B C$ ， $B D ⊥ C E$ ， $A E ⊥ C E$ ，垂足分别为D、E点， $B D = 5 cm$ ， $D E = 3 cm$ ．则 $A E$ 的长是（）

A、 $1 cm$ B、 $2cm$ C、 $3 cm$ D、 $4 cm$

查看解析
8、点 $P (3, - 4)$ 关于y轴的对称点 $P^{'}$ 的坐标是（）．

A、 $(- 3, - 4)$ B、 $(3, 4)$ C、 $(- 3, 4)$ D、 $(- 4, 3)$

查看解析
9、下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看解析
10、先化简，再求值： $3 x^{2} + (x y - 3 y^{2}) - 2 (x^{2} + x y - 2 y^{2})$ ，其中 $x = 1 ， y = - 2$ ．

查看解析
11、计算： ${(- 1)}^{2024} + |2 - (- 3)| + 3 \div (- \frac{3}{2})$ ．

查看解析
12、在数轴上表示a，0，b三个数的点如图所示，已知 $O A = O B$ ，则化简 $|a + b| + |\frac{a}{b}| + 2 |a + 1| =$

查看解析
13、用四舍五入法将 $2.336$ 精确到 $0.01$ ，所得到的近似数是．

查看解析
14、如图，将数列排成一个三角形数阵：

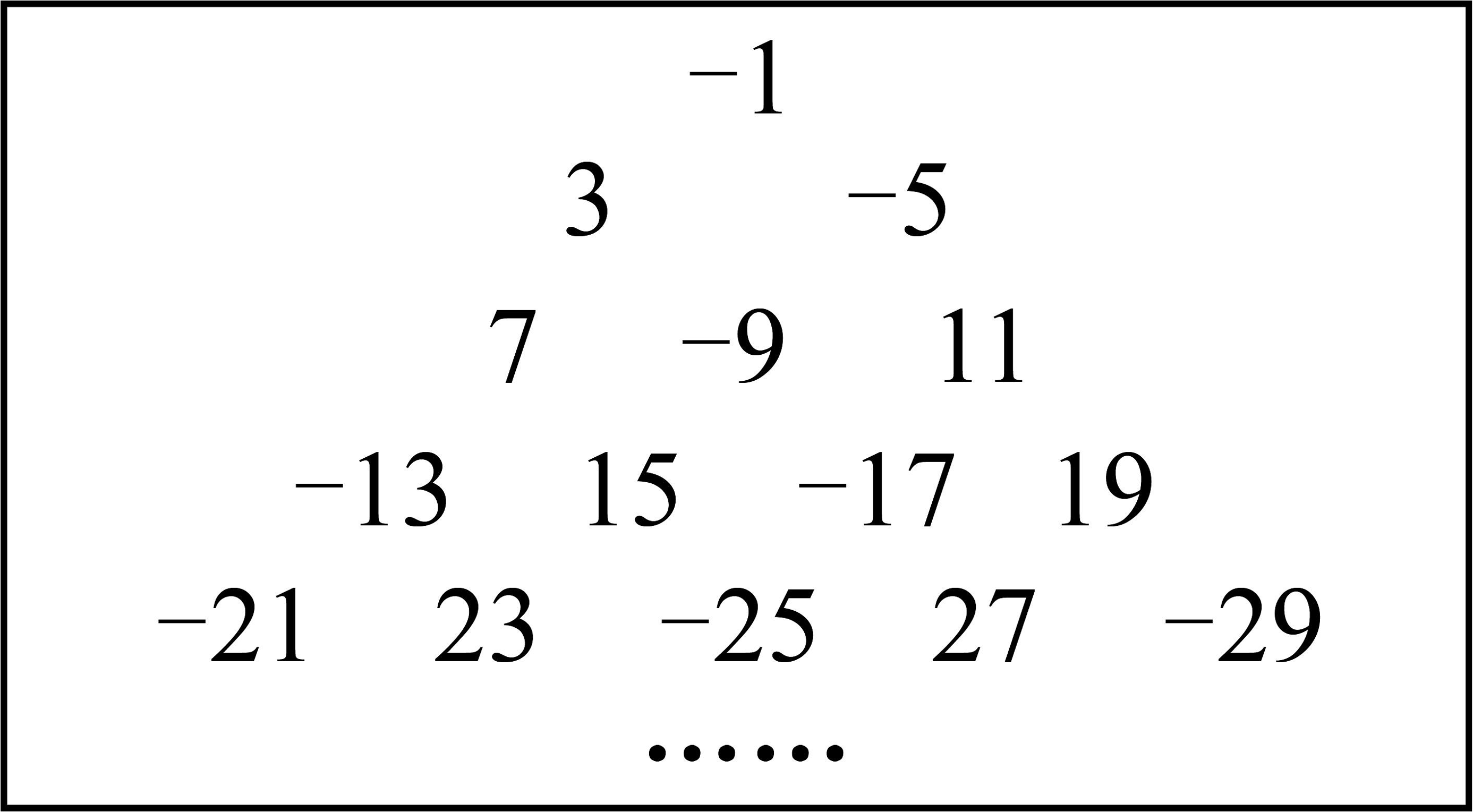
按照以上排列的规律，第11行从左数第5个数为（）

A、119 B、－121 C、－117 D、123

查看解析
15、有8筐白菜，以每筐20千克为标准，超过的千克数记作正数，称重后的记录如下：
$1.5$ ， $- 3$ ， 2， $- 0.5$ ， 1， $- 2$ ， 2， $- 2.5$
回答下列问题：

(1)、这8筐白菜中最接近标准重量时这筐白菜重_____千克．

(2)、这8筐白菜中最重的重_____千克；最轻的重_____千克．

(3)、若白菜每千克售价2元，则出售这8筐白菜可卖多少元？

查看解析
16、若 $a$ 与 $b$ 互为相反数且b≠0， $c$ 、 $d$ 互为倒数， $|m| = 1$ ，则 $\frac{a + b}{2008} - c d + \frac{a}{b} - m^{2}$ 的值是．

查看解析
17、等腰 $Rt △ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，点 $A$ 、点 $B$ 分别是 $y$ 轴、 $x$ 轴上两个动点，直角边 $A C$ 交 $x$ 轴于点 $D$ ，斜边 $B C$ 交 $y$ 轴于点 $E$ ．

(1)、如图（1），已知 $C$ 点的横坐标为 $- 1$ ，直接写出点 $A$ 的坐标；

(2)、如图（2），当等腰 $Rt △ A B C$ 运动到使点 $D$ 恰为 $A C$ 中点时，连接 $D E$ ，求证： $∠ A D B = ∠ C D E$ ；

(3)、如图（3），若点 $A$ 在 $x$ 轴上，且 $A (- 4 ， 0)$ ，点 $B$ 在 $y$ 轴的正半轴上运动时，分别以 $O B$ 、 $A B$ 为直角边在第一、二象限作等腰直角 $△ B O D$ 和等腰直角 $△ A B C$ ，连接 $C D$ 交 $y$ 轴于点 $P$ ，问当点 $B$ 在 $y$ 轴的正半轴上运动时， $B P$ 的长度是否变化?若变化请说明理由，若不变化，请求出 $B P$ 的长度．

查看解析
18、如图，在等腰△ABC中，CA＝CB，点D，E，F分别是AC，BC，AB上的点，且AF＝BE，∠DFE＝∠A，连DE，GF平分∠DFE，求证：GF⊥DE．

查看解析
19、如图，是一个8×10正方形格纸， $△$ ABC中A点坐标为(﹣2，1)，B点的坐标为(﹣1，2)．

(1)、请在图中建立平面直角坐标系，指出 $△$ ABC和 $△ A^{'} B^{'} C^{'}$ 关于哪条直线对称？（直接写答案）

(2)、作出 $△$ ABC关于x轴对称图形 $△ A_{1} B_{1} C_{1}$ ；请直接写出 $A^{'}$ 、 $B^{'}$ 、 $C^{'}$ 三点坐标．

(3)、在x轴上求作一点M，使 $△ A B^{'} M$ 的周长最小，请直接写出M点的坐标．

查看解析
20、如图，在 $△ A B C$ 中， $D$ 是边 $B C$ 的中点， $D E ⊥ A C$ ， $D F ⊥ A B$ ，垂足分别为 $E$ ， $F$ ，且 $C E = B F$ ．求证： $A F = A E$ ．

查看解析

上一页 1065 1066 1067 1068 1069 下一页跳转