相关试卷

1、一次函数 $y = 5 - x$ 与 $y = k x - 1$ 图象的交点为A $(m, 3)$ ，则方程组 ${\begin{array}{l} x + y = 5 \\ 2 x - y = 1 \end{array}$ 的解为．

查看解析
2、一次函数 $y = (2 m - 2) x + 3 - m$ 的图像不经过第四象限，则m的取值范围是．

查看解析
3、已知函数 $y = (m - 1) x^{| m |} - 2024$ 是关于 $x$ 的一次函数，则 $m$ 的值为．

查看解析
4、徽园，是一座采用皇家园林、徽派建筑、现代简约等多种风格设计、展示安徽各地文化，将观光与文化融为一体的大型综合性观光公园．周末我校八年级三位老师带领x名学生到徽园参观研学，已知成人票每张20元，学生票每张10元，设门票的总费用为y元，则y与x之间的关系式为．

查看解析
5、如图，函数 $y = - x + 2$ 的图像与x轴、y轴分别交于点A ， B ，若直线 $B C$ 将 $△ A O B$ 分为面积比为 $1 : 3$ 的两部分，则直线 $B C$ 的函数表达式为（）

A、 $y = - \frac{4}{3} x + 2$ 或 $y = - 2 x + 2$ B、 $y = - 2 x + 2$ C、 $y = - \frac{4}{3} x + 2$ 或 $y = - 4 x + 2$ D、 $y = - \frac{4}{3} x + 2$

查看解析
6、如图，在平面直角坐标系中，点 $A$ 的坐标为 $(0, 3)$ ， $△ O A B$ 沿 $x$ 轴向右平移后得到 $△ O^{^{'}} A^{^{'}} B^{^{'}}$ ，点 $A$ 的对应点 $A^{'}$ 在直线 $y = \frac{3}{4} x$ 上，则点 $B$ 与其对应点 $B^{'}$ 之间的距离（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、3 D、4

查看解析
7、对于一次函数 $y = - x + 3$ 的相关性质，下列描述错误的是（）

A、函数图象经过第一、二、四象限 B、函数图象与x轴的交点坐标为 $(0, 3)$ C、y随x的增大而减小 D、函数图象与坐标轴围成的三角形面积为 $\frac{9}{2}$

查看解析
8、若函数 $y = - 7 x + m - 2$ 是正比例函数，则m的值为（）

A、0 B、1 C、 $- 1$ D、2

查看解析
9、函数 $y = \frac{x + 1}{x - 1}$ 中，自变量x的取值范围是（）．

A、 $x \neq 0$ B、 $x \neq 1$ C、 $x > 1$ D、 $x < 1$

查看解析
10、函数 $y = \frac{1}{\sqrt{2 - 3 x}}$ 中，自变量 $x$ 的取值范围是（）

A、 $x \geq \frac{2}{3}$ B、 $x > \frac{2}{3}$ C、 $x < \frac{2}{3}$ D、 $x \leq \frac{2}{3}$

查看解析
11、一条笔直的公路上依次有A、B、C三地，甲车从A地驶往C地，乙车从A地驶往B地，两车同时出发并以各自的速度匀速行驶，乙车中途因故障停下来修理，修好后立即以原速的两倍继续前进到达B地；如图是甲、乙两车与A地的距离y（千米）（小时）之间的大致图象．下列说法错误的是（）

A、甲车的速度为 $60 k m / h$ B、B、C两地之间的距离 $60 k m$ ； C、 $4.5 h$ 后乙追上甲 D、当两车相距40千米时，甲车行驶了 $\frac{7}{3} h$ 或 $3.5 h$ ．

查看解析
12、元朝朱世杰的《算学启蒙》一书中，记载了一个驽马先行的问题，其中良马与劣马行走路程 $s$ （单位：里）关于行走时间 $t$ （单位：日）的函数图象如图所示，下列说法：①良马的速度比劣马的速度快80里/日；②劣马比良马早出发12日；③点 $A$ 表示的实际意义是劣马出发32日时，良马追上劣马．其中正确的是（）

A、①②③ B、①③ C、②③ D、①②

查看解析
13、下列图像中，表示 $y$ 是 $x$ 的函数的是（）

A、 B、 C、 D、

查看解析
14、某中学为选拔“校园形象代言人”，先后进行了笔试和面试．在笔试中，甲、乙、丙三位同学脱颖而出，他们的笔试成绩（满分为100分）分别是87，85，90．在面试中，十位评委对甲、乙、丙三位同学的表现进行打分，每位评委最高打10分，面试成绩等于各位评委打分之和．对三位同学的面试数据进行整理、描述和分析，并给出了相关信息．
c．甲、乙、丙三位同学面试情况统计表
同学
评委打分的中位数
评委打分的众数
面试成绩
方差
甲
m
9和10
85
1.85
乙
8.5
8
87
$s^{2}$
丙
8
n
p
2.01
根据以上信息，回答下列问题：

(1)、 $m =$ $n =$ ；

(2)、求丙同学的面试成绩 $p$ ；

(3)、通过比较方差，可判断评委对学生面试表现评价的一致性程度．据此推断评委对同学的评价更一致（填“甲”、“乙”或“丙”）；

(4)、按笔试成绩占 $40 %$ ，面试成绩占 $60 %$ 选出综合成绩最高的同学是（填“甲”、“乙”或“丙”）．

查看解析
15、某校组织学生参加“防疫卫生知识竞赛”，为了解竞赛情况，从两个年级各抽取10名学生的成绩（满分为100分）．收集数据如下：
七年级：90，95，95，80，85，90，80，90，85，100；
八年级：85，85，95，80，95，90，90，90，100，90．
分析数据：
　
平均数
中位数
众数
方差
七年级
89
m
90
39
八年级
n
90
p
q
根据以上信息回答下列问题：

(1)、 $m =$ ， $n =$ ， $p =$ ；

(2)、从方差的角度来判断哪个年级的成绩更稳定？写出理由；

(3)、通过数据分析，你认为哪个年级的成绩比较好？说明理由．

查看解析
16、已知有四个有理数： $- 9 ， - 3$ ， 2，6．

(1)、计算： $- 9 + (- 3) - 6 \div 2$ ；

(2)、若 $(- 9) \div (- 3) \times 2 □ 6 = 12$ ，请推算□内的运算符号；

(3)、若再添加一个有理数 $m$ ，使 $- 9 ， - 3$ ， 2，6与 $m$ 这五个数的平均数为 $- 2$ ，求 $m$ 的值．

查看解析
17、甲、乙两名同学5次立定跳远成绩的平均值都是 $2.42 m ， s^{2}_{甲} = 0.04 ， s^{2}_{乙} = 0.13$ ，这两名同学成绩比较稳定的是．（填“甲”或“乙”）

查看解析
18、甲、乙、丙、丁四名运动员参加射击项目选拔赛，每人10次射击成绩的平均数 $\bar{x}$ （单位：环）和方差 $s^{2}$ 如下表所示：

甲
乙
丙
丁

$\bar{x}$
9.5
9.5
8.2
8.5

$s^{2}$
0.09
0.65
0.09
2.85
根据表中数据，从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（　　）

A、甲 B、乙 C、丙 D、丁

查看解析
19、已知点 $O$ 为直线 $A B$ 上一点，过点 $O$ 作射线 $O C$ ，使 $∠ B O C = 60^{\circ}$ .将一直角三角板的直角顶点放在点 $O$ 处.

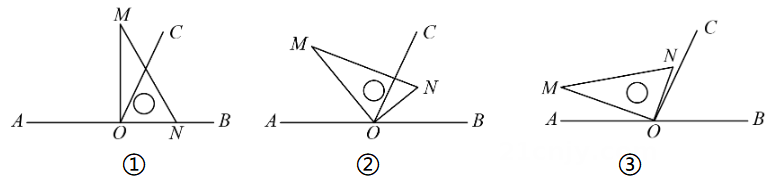(1)、如图①，当三角板 $M O N$ 的一边 $O N$ 与射线 $O B$ 重合时， $∠ M O C =$ .

(2)、如图②，将图①中的三角板 $O M N$ 绕点 $O$ 以每秒 $15^{\circ}$ 的速度按逆时针方向旋转一周，在旋转的过程中，当直线 $O N$ 恰好平分锐角 $∠ B O C$ 时，旋转的时间是多少秒？

(3)、将三角板 $M O N$ 绕点 $O$ 逆时针旋转至图③时， $∠ N O C = 5^{\circ}$ ，求 $∠ A O M$ 的度数.

查看解析
20、一个点在有公共端点的两条线段组成的一条折线上，且把这条折线分成长度相等的两部分，这个点叫作这条折线的“折中点”.如图所示，如果点 $D$ 是折线 $A - C - B$ 的“折中点”，请解答以下问题：

(1)、当 $A C > B C$ 时，点 $D$ 在线段上；

(2)、当点 $D$ 与点 $C$ 重合时，直接比较 $A C$ ， $B C$ 的长度；

(3)、若 $E$ 为线段 $A C$ 的中点， $E C = 4$ ， $C D = 3$ ，求 $B C$ 的长度.

查看解析

上一页 476 477 478 479 480 下一页跳转

同学	评委打分的中位数	评委打分的众数	面试成绩	方差
甲	m	9和10	85	1.85
乙	8.5	8	87	$s^{2}$
丙	8	n	p	2.01

	平均数	中位数	众数	方差
七年级	89	m	90	39
八年级	n	90	p	q

	甲	乙	丙	丁
$\bar{x}$	9.5	9.5	8.2	8.5
$s^{2}$	0.09	0.65	0.09	2.85