-
1、【教材呈现】“整体思想”是数学解题中一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.下题是华师版七年级上册数学教材第120页的部分内容.
代数式的值为7,则代数式的值为▲ .
【阅读理解】小明在做作业时采用的方法如下:由题意得,则有 , , 所以代数式的值为5.
(1)、【方法运用】若代数式的值为15,求代数式的值.
(2)、若时,代数式的值为19,当时,求代数式的值.(3)、【拓展应用】若 , . 则的值为 .
-
2、点在数轴上的位置如图所示,其对应的数分别是和 .
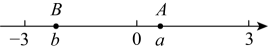 (1)、化简:;(2)、若 , 到的距离是1个单位长度,、互为相反数,、互为倒数,求代数式的值.
(1)、化简:;(2)、若 , 到的距离是1个单位长度,、互为相反数,、互为倒数,求代数式的值. -
3、已知多项式 , .(1)、若的值与x的取值无关,求m,n的值;(2)、在(1)的条件下,求的值.
-
4、已知代数式 .(1)、化简;(2)、若满足等式 , 求的值.
-
5、如图,小长方形纸片的长为a,宽为b,且 , 将7张纸片按图示不重叠的放在长方形内,未被覆盖的部分恰好被分割为两个长方形,面积分别为和 .
 (1)、当 , , 时,的值为 ;(2)、若长度保持不变,变长,将这7张小长方形纸片还按照同样的方式放在新的长方形内,当的值与的长度无关时,a、b满足的关系式是 .
(1)、当 , , 时,的值为 ;(2)、若长度保持不变,变长,将这7张小长方形纸片还按照同样的方式放在新的长方形内,当的值与的长度无关时,a、b满足的关系式是 . -
6、设一列数 , , , …, , …中任意三个相邻的数之和都是 , 已知 , , , 那么的值是 .
-
7、若关于的多项式中不含一次项,则的值是 .
-
8、已知 , 当时,的值是 .
-
9、如图,两个正方形的面积分别为16、9,两阴影部分的面积分别为 , 则等于( )
 A、7 B、8 C、9 D、10
A、7 B、8 C、9 D、10 -
10、用菱形按如图所示的规律拼图案,其中第①个图案中有2个菱形,第②个图案中有5个菱形,第③个图案中有8个菱形,第④个图案中有11个菱形,…,按此规律,则第⑩个图案中,菱形的个数是( )
 A、26 B、27 C、29 D、32
A、26 B、27 C、29 D、32 -
11、已知多项式是关于的三次三项式,则m的值等于( )A、 B、1 C、 D、以上都不对
-
12、要使关于x的多项式化简后不含x的二次项,则m的值是( ).A、 B、4 C、 D、6
-
13、已知a,b,c的大小关系如图所示,则下列三个结论中正确的个数是( )
①;②;③ .
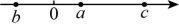 A、0个 B、1个 C、2个 D、3个
A、0个 B、1个 C、2个 D、3个 -
14、“这么近那么美,周末到河北”.某校组织了师生y人来到白洋淀划船游玩,租用的每条船可乘坐x人,全部上船后,发现租用的游船只剩一个空位.用含x,y的代数式表示该校租用游船的数量为( )A、条 B、条 C、条 D、条
-
15、已知:当时,代数式的值为10;那么当时,代数式的值为( )A、-10 B、- 4 C、10 D、2
-
16、下列说法正确的是( )A、的系数是 B、单项式的系数是1,次数是1 C、是二次三项式 D、的次数是6
-
17、下列计算中,正确的是( )A、 B、 C、 D、
-
18、给出定义如下:若点满足 , 则称这个点为“秀点”,如: , 故点是“秀点”.(1)、点 , 点 , 点中,是“秀点”的是;(2)、若点是“秀点”,求的值;(3)、是否存在点 , 使点是“秀点”,若存在,求出的值;若不存在,说明理由.
-
19、我们知道,是一个无理数,无理数是无限不循环小数,若将这个数减去它的整数部分,差就是小数部分,即的整数部分是1,则小数部分是.请回答以下问题:(1)、已知为的整数部分,是的小数部分,则 , .(2)、若 , 其中是整数,且 , 求的算术平方根.
-
20、一块长方形空地面积为 , 其长、宽之比为.
 (1)、求这块长方形空地的周长;(2)、如图,在空地内修建“字型”走道(横向走道宽度不变)后将空地分割成两个花坛(花坛1为正方形,花坛2为长方形,其长、宽之比为),花坛的总面积为 , 宽度为的农药喷洒车能不能在走道上正常通行?
(1)、求这块长方形空地的周长;(2)、如图,在空地内修建“字型”走道(横向走道宽度不变)后将空地分割成两个花坛(花坛1为正方形,花坛2为长方形,其长、宽之比为),花坛的总面积为 , 宽度为的农药喷洒车能不能在走道上正常通行?