-
1、(1)、计算：(2)、先化简，再求值： 其中x=2.
-
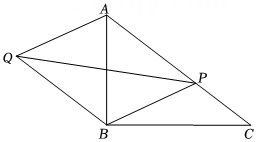
2、如图， 在 Rt△ABC 中， ∠ABC=90°， AB=6， BC=8.点P 为边 AC上异于 A的一点，以PA，PB 为邻边作▱PAOB，则线段PQ的最小值是.
-
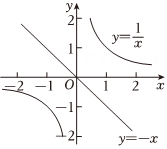
3、取直线y=-x上一点 A(x1 ， y1)， ①过点 A1作x轴的垂线， 交 于点 A(x2 ， y2)； ②过点 A2作y轴的垂线， 交y=-x 于点 A3(x3 ， y3)；
如此循环进行下去.
按照上面的操作，若点 A1的坐标为(1，-1)，则点 A2025的坐标是.
-
4、在平面直角坐标系中，将点 P(3，4)向下平移2个单位长度，得到的对应点P'的坐标是.
-
5、 在水分、养料等条件一定的情况下，某植物的生长速度y(厘米/天)和光照强度x(勒克斯)之间存在一定关系.在低光照强度范围(200≤x<1000)内，y与x近似成一次函数关系；在中高光照强度范围(x≥1000)内，y与x近似成二次函数关系.其部分图象如图所示.根据图象，下列结论正确的是（ ）
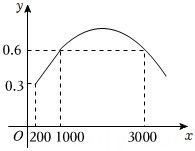A、当x≥1000时， y随x的增大而减小 B、当x=2000时， y有最大值 C、当y≥0.6时， x≥1000 D、当y=0.4时， x=600 -
6、如图，在平面直角坐标系中，A，C两点在坐标轴上，四边形OABC是面积为4的正方形.若函数 的图象经过点 B，则满足y≥2的x的取值范围为（ ）
A、0<x≤2 B、x≥2 C、0<x≤4 D、x≥4 -
7、 在中国古代文化中，玉璧寓意宇宙的广阔与秩序，也经常被视为君子修身齐家的象征.下图是某玉璧的平面示意图，由一个正方形的内切圆和外接圆组成.已知内切圆的半径是2，则图中阴影部分的面积是（ ）
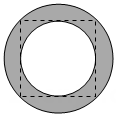A、π B、2π C、3π D、4π -
8、明代数学家吴敬的《九章算法比类大全》中有一个“哪吒夜叉”问题，大意是：有3个头6只手的哪吒若干，有1个头8只手的夜叉若干，两方交战，共有36个头，108只手.问哪吒、夜叉各有多少?设哪吒有x个，夜叉有y个，则根据条件所列方程组为（ ）A、 B、 C、 D、
-
9、已知a≠0，则下列运算正确的是（ ）A、-2a+3a=5 B、 C、 D、
-
10、好客山东以其宽厚仁德的人文情怀、风景秀丽的河海山川吸引了来自世界各地的朋友，据统计，山东省2024年全年接待游客超9亿人次.数据“9亿”用科学记数法表示为（ ）A、 B、0.9×108 C、9×108 D、0.9×109
-
11、我国“深蓝2号”大型智能深海养殖网箱的主体是一个正六棱柱，其示意图的主视图是（ ）
A、
B、
C、
D、
-
12、下列图形中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
-
13、如图，在中， ， M、N、K分别是 ， ， 上的点，且 ， ． 若 ， 则的度数为 ．
-
14、如图，在△ABC中，AB=2，∠ACB=90°，则△ABC 周长的最大值为.
-
15、如图，正方形ABCD 的边长为4，动点 E，F分别从点A，C同时出发，以相同的速度分别沿AB，CD 向终点B，D 移动，当点 E 到达点 B 时，运动停止.过点 B 作直线EF 的垂线BG，垂足为G，连接AG，则AG 的最小值为.
-
16、如图，在四边形ABCD中，∠DAB=∠ABC=90°，AD=AB=1，BC=2，点 P 为射线 DA 上的一动点，过B，D，P 三点的圆交PC 于点Q，则 DQ的最小值为.
-
17、如图，AB 是⊙O 的弦，.AB=6 ， ∠AOB=120°，C 为⊙O上的一动点，D，E 分别是AC，OB 的中点，连接DE，则线段 DE 的取值范围是.
-
18、如图，在平面直角坐标系中，菱形ABDC的边AB 在x 轴上，顶点 C 在y 轴上，A(-3，0)，C(0，4)，抛物线 经过点C，且顶点 M 在直线BC 上，则a 的值为 ( )
A、 B、 C、 D、 -
19、如图，二次函数 bx+c 的图象与x 轴交于A，B 两点，与y轴交于点C，其中A(-2，0)，C(0，-2).
(1)、求二次函数的表达式.(2)、若P 是二次函数图象上的一点，且点 P 在第二象限，线段 PC 交x轴于点D，△PDB 的面积是△CDB 的面积的2倍，求点 P 的坐标. -
20、某果商以每吨2万元的价格收购早熟荔枝，销往国外，若按每吨5万元的价格出售，平均每天可出售100 吨.市场调查显示：如果每吨每降价1万元，那么每天的销售量相应增加50吨.该果商如何定价才能使每天的利润最大?最大利润是多少万元?