相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、在四面体ABCD中, , , , M,N分别为棱AB,CD所在直线的点,则线段长度的最小值为 .
-
2、已知空间5个点A,B,C,D,P,且A,B,C,D共面,若且 , , 则的最小值为 .
-
3、已知直线l的方程为 , 则直线l过定点.
-
4、在空间直角坐标系中,已知向量 , 点 , 点 .
(1)若直线l经过点 , 且以方向向量,P是直线l上的任意一点,则直线l的方程为;
(2)若平面经过最 , 且以为法向量,P是平面内的任意一点,则平面的方程为 .
如图,一在棱长为1的正方体中,以O为坐标原点,建立如图所示的空间直角坐标系,则下列说法正确的是( )
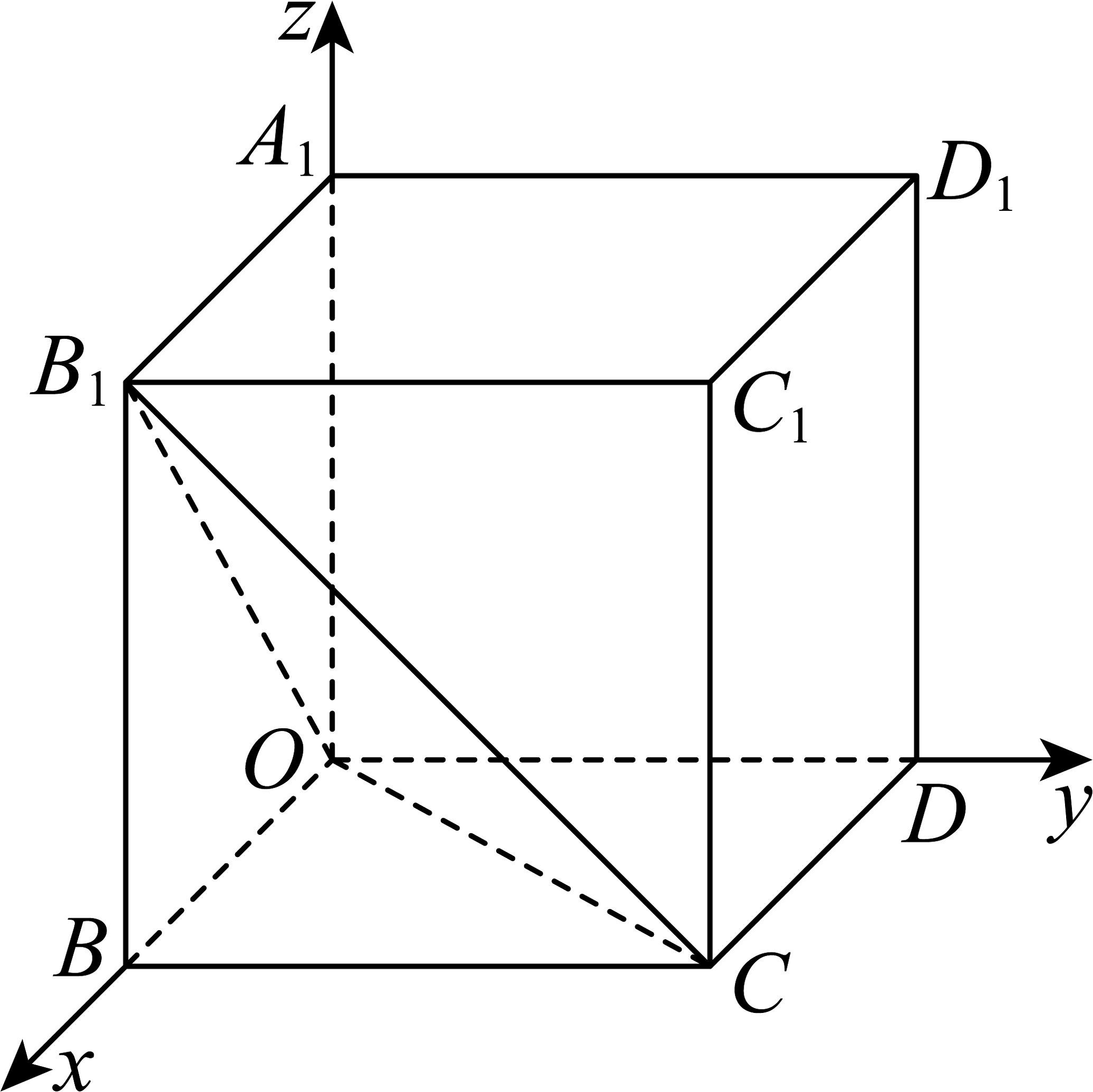 A、平面的法向量为 B、直线的方程为 C、过点的平面方程为 , 则平面截正方体所得截面的面积为 D、平面方程为 , 平面方程为 , 则平面与平面之间的距离为
A、平面的法向量为 B、直线的方程为 C、过点的平面方程为 , 则平面截正方体所得截面的面积为 D、平面方程为 , 平面方程为 , 则平面与平面之间的距离为 -
5、已知直线和为函数()图象上两条相邻的对称轴.则下列说法正确的是( )A、 B、 C、若 , 则图象可以由图象向左平移个单位得到 D、若 , 则在区间上的值域为
-
6、在中,角A,B,C所对的边分别为a,b,c,则下列条件能确定2个三角形的是( )A、 , , B、 , , C、 , , D、 , ,
-
7、函数 , 若关于x的方程有三个不同的实数根,则实数m的取值范围是( )A、 B、 C、 D、
-
8、已知实数x,y满足 , 且 , 则不可能是( )A、-3 B、-4 C、3 D、4
-
9、已知函数在R上单调递增,则a的取值范围是( )A、 B、 C、 D、
-
10、直线l:(参数,)的倾斜角的取值范围是( )A、 B、 C、 D、
-
11、已知一组数据的平均数 , 方差 , 则数据的平均数、方差分别为( )A、16,20 B、16,80 C、18,20 D、18,80
-
12、下列结论中,错误的结论有( )A、取得最大值时的值为 B、若 , 则的最大值为 C、函数的最小值为 D、若 , , 且 , 那么的最小值为
-
13、高一共50名学生参加100米和400米两项体育测试并且每人至少有一项合格,100米和400米两项测试成绩合格的分别有29人和25人,则这两项成绩都合格的人数是( )A、3 B、4 C、5 D、9
-
14、若为定义在上的函数,且关于原点对称,则“存在 , 使得”是“函数为非奇非偶函数”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件
-
15、对于数列 , 如果存在正整数 , 当任意正整数时均有 , 则称为的“项递增相伴数列”.若可取任意的正整数,则称为的“无限递增相伴数列”.(1)、已知 , 请写出一个数列的“无限递增相伴数列”,并说明理由?(2)、若满足 , 其中是首项的等差数列,当为的“无限递增相伴数列”时,求的通项公式:(3)、已知等差数列和正整数等比数列满足: , 其中k是正整数,求证:存在正整数k,使得为的“2024项递增相伴数列”.
-
16、已知函数.(1)、若函数在处切线的斜率为 , 求实数的值;(2)、当时,恒成立,求实数的最大值;(3)、当时,证明:
-
17、如图1,在五边形中, , , 且 , 将沿折成图2,使得 , 为的中点.
 (1)、证明:平面;(2)、若与平面所成的角为 , 求二面角的正弦值.
(1)、证明:平面;(2)、若与平面所成的角为 , 求二面角的正弦值. -
18、在一次考试中某班级50名学生的成绩统计如表,规定75分以下为一般,大于等于75分小于85分为良好,85分及以上为优秀.
分数
69
73
74
75
77
78
79
80
人数
2
4
4
2
3
4
6
3
分数
82
83
85
87
89
93
95
合计
人数
3
4
4
5
2
3
1
50
经计算样本的平均值 , 标准差.为评判该份试卷质量的好坏,从其中任取一人,记其成绩为 , 并根据以下不等式进行评判.
①;②;③.
评判规则:若同时满足上述三个不等式,则被评为优秀试卷;若仅满足其中两个不等式,则被评为合格试卷;其他情况,则被评为不合格试卷.
(1)、试判断该份试卷被评为哪种等级;(2)、按分层随机抽样的方式从3个层次的学生中抽出10名学生,再从抽出的10名学生中随机抽出4人进行学习方法交流,用随机变量表示4人中成绩优秀的人数,求随机变量的分布列和均值. -
19、现有标号依次为的盒子,标号为1的盒子里面有2个红球和2个白球,其余盒子里都是1个红球和1个白球.现从1号盒子里面取出2个球放入2号盒子,再从2号盒子里面取出2个球放入3号盒子,则3号盒子里面是2个红球和2个白球的概率为.
-
20、设曲线和曲线在它们的公共点处有相同的切线,则的值为.