高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
试卷更新日期:2018-02-27 类型:同步测试
一、选择题
-
1. 已知变量x,y之间具有线性相关关系,其散点图如图所示,回归直线l的方程为 ,则下列说法正确的是( )
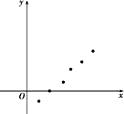 A、 >0, <0 B、 >0, >0 C、 <0, <0 D、 <0, > 02. 有五组变量:
A、 >0, <0 B、 >0, >0 C、 <0, <0 D、 <0, > 02. 有五组变量:①汽车的重量和汽车每消耗1升汽油所行驶的平均路程;
②平均日学习时间和平均学习成绩;
③某人每日吸烟量和身体健康情况;
④圆的半径与面积;
⑤汽车的重量和每千米耗油量.
其中两个变量成正相关的是( )
A、①③ B、②④ C、②⑤ D、④⑤3. 四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:①y与x负相关且 =2.347x-6.423;②y与x负相关且 =-3.476x+5.648;
③y与x正相关且 =5.437x+8.493;④y与x正相关且 =-4.326x-4.578.
其中一定不正确的结论的序号是( )
A、①② B、②③ C、③④ D、①④4. 为研究语文成绩和英语成绩之间是否具有线性相关关系,统计两科成绩得到如图所示的散点图(两坐标轴单位长度相同),用回归直线 = x+ 近似地刻画其相关关系,根据图形,以下结论最有可能成立的是( )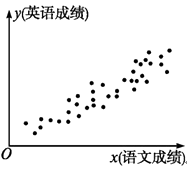 A、线性相关关系较强, 的值为3.25 B、线性相关关系较强, 的值为0.83 C、线性相关关系较强, 的值为-0.87 D、线性相关关系太弱,无研究价值5. 某产品的广告费用x与销售额y的统计数据如下表:
A、线性相关关系较强, 的值为3.25 B、线性相关关系较强, 的值为0.83 C、线性相关关系较强, 的值为-0.87 D、线性相关关系太弱,无研究价值5. 某产品的广告费用x与销售额y的统计数据如下表:广告费用x(万元)
4
2
3
5
销售额y(万元)
49
26
39
54
根据上表可得回归方程 = x+ 中的 为9.4,据此模型预报广告费用为6万元时销售额为( )
A、63.6万元 B、65.5万元 C、67.7万元 D、72.0万元6. 某商店对每天进店人数x与某种商品成交量y(单位:件)进行了统计如下表,由表中数据,得线性回归方程为 = x-3.25.如果某天进店人数是75,预测这一天该商品销售的件数为( )x
10
15
20
25
30
35
40
y
5
6
12
14
20
23
25
A、47 B、52 C、55 D、387. 已知x与y之间的几组数据如下表,根据表中数据所得线性回归直线方程为 = x+ ,某同学根据表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )x
1
2
3
4
5
6
y
0
2
1
3
3
4
A、 >b′, >a′ B、 >b′, <a′ C、 <b′, >a′ D、 <b′, <a′二、单选题
-
8. 已知x、y取值如下表:
x
0
1
4
5
6
8
y
1.3
1.8
5.6
6.1
7.4
9.3
从所得的散点图分析可知:y与x线性相关,且 =0.95x+a,则a=( )
A、1.30 B、1.45 C、1.65 D、1.80三、填空题
-
9. 调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程: =0. 254x+0. 321. 由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加万元.10. 已知施化肥量x与水稻产量y的试验数据如下表,则变量x与变量y是相关(填“正”或“负”).
施化肥量x
15
20
25
30
35
40
45
水稻产量y
330
345
365
405
445
450
455
11. 高三某班学生每周用于物理学习的时间x(单位:小时)与物理成绩y(单位:分)之间的关系如下表,根据下表可得回归方程的斜率为3.53,则回归直线在y轴上的截距为 . (答案保留到0.1)x
24
15
23
19
16
11
20
16
17
13
y
92
79
97
89
64
47
83
68
71
59
四、解答题
-
12. 要分析学生初中升学考试的数学成绩对高一年级数学学习有什么影响,在高一年级学生中随机抽取10名学生,分析他们入学的数学成绩(x)和高一年级期末数学考试成绩(y)(如下表):
编号
1
2
3
4
5
6
7
8
9
10
x
63
67
45
88
81
71
52
99
58
76
y
65
78
52
85
92
89
73
98
56
75
(1)、画出散点图;(2)、判断入学成绩(x)与高一期末考试成绩(y)是否有线性相关关系;(3)、如果x与y具有线性相关关系,求出回归直线方程;13. 一台机器由于使用时间较长,生产的零件有一些缺损,按不同转速生产出来的零件有缺损的统计数据如下表所示.转速x(转/秒)
16
14
12
8
每小时生产有缺损零件数y(个)
11
9
8
5
(1)、作出散点图;(2)、如果y与x线性相关,求出回归直线方程;(3)、若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器的运转速度应控制在什么范围内?14. 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.x
3
4
5
6
y
2.5
3
4
4.5
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
(1)、请画出上表数据的散点图;(2)、请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;(3)、已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤.
-