相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、设 , 向量 , , , 且 , , 则( ).A、 B、 C、5 D、6
-
2、如图,在平行六面体中,点M为与的交点,若 , , , 则下列向量中与相等的向量是( ).
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、若构成空间的一个基底,则下列选项中可以构成基底的是( )A、 , , B、 , , C、 , , D、 , ,
-
4、给出下列命题:
①若空间向量满足 , 则;
②在正方体中,必有;
③若空间向量满足 , 则 .
其中假命题的个数是( )
A、0 B、1 C、2 D、3 -
5、下列函数中,在上单调递增的是( )A、 B、 C、 D、
-
6、设全集 , 集合 , , 则( )A、 B、 C、 D、
-
7、设为虚数单位,若复数 , 则复数的实部为( )A、 B、 C、 D、
-
8、已知向量 , 且 , 则的值为( )A、4 B、2 C、3 D、1
-
9、已知平面向量 , 满足 , , 且在上的投影向量为 , 则为.
-
10、已知平面直角坐标系中,圆 , 点 ,(1)、若是圆上的动点,线段的中点为 , 求的轨迹方程;(2)、以为直径的圆交圆于 , 两点,求.
-
11、如图,在直三棱柱中,底面是等腰三角形, , , , 分别是棱 , 的中点.
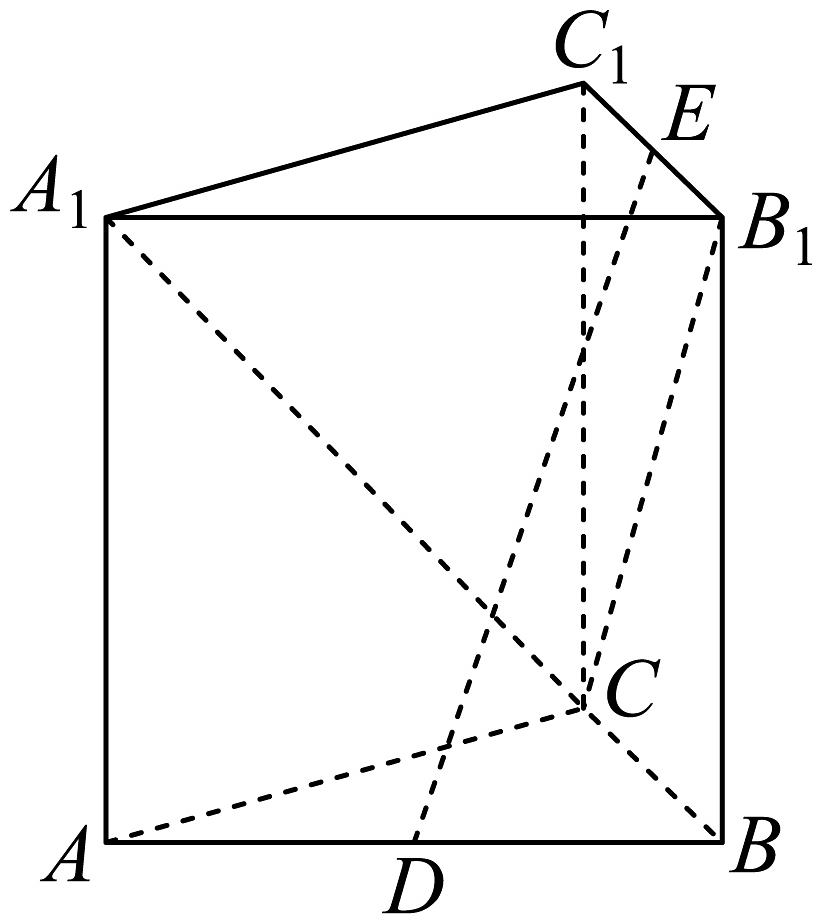 (1)、求证:平面;(2)、求直线与平面所成的角的正弦值.
(1)、求证:平面;(2)、求直线与平面所成的角的正弦值. -
12、在平面直角坐标系中,已知圆 , 直线 , 过上一点作圆的切线,切点为A,则的最小值为.
-
13、已知正三角形的边长为1,在平面内,若向量满足 , 则的最大值为( )A、 B、 C、2 D、3
-
14、已知点 , 平面 , 其中 , 则点到平面的距离是( )A、 B、 C、2 D、3
-
15、已知 , 是两个不重合的平面,且直线 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
16、解关于x的不等式.(1)、();(2)、 .
-
17、已知集合.(1)、当时,求;(2)、求.
-
18、设函数.(1)、若命题:是假命题,求的取值范围;(2)、若存在 , 使得成立,求实数的取值范围.
-
19、已知实数满足 , 且 , 若关于的不等式恒成立,则实数的取值范围是 .
-
20、已知 , 则下列不等式一定成立的是( )A、 B、 C、 D、