相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、给出下列四个命题,其中正确命题的是( )A、若 , 则; B、若 , 则; C、若 , 则; D、若 , 则.
-
2、已知是定义在上的偶函数,对任意的满足且 , 则不等式的解集为( )A、 B、 C、 D、
-
3、若命题“对任意 , 使得成立”是真命题,则实数a的取值范围是( )A、 B、 C、 D、
-
4、已知函数 , 则 ( )A、 B、 C、1 D、
-
5、函数的定义域是( )A、 B、 C、 D、
-
6、已知集合 , , 则图中阴影部分表示的集合为
 A、 B、 C、 D、
A、 B、 C、 D、 -
7、为鼓励青年大学生积极参与暑期社会实践,某高校今年暑假组织返乡大学生积极参与了当地的暑假社区儿童托管服务.现抽样调查了其中100名大学生,统计他们参加社区托管活动的时间(单位:小时),并将统计数据制成如图所示的频率分布直方图.另外,根据参加社区托管活动的时间从长到短按3:4:3的比例分别被评为优秀、良好、合格.
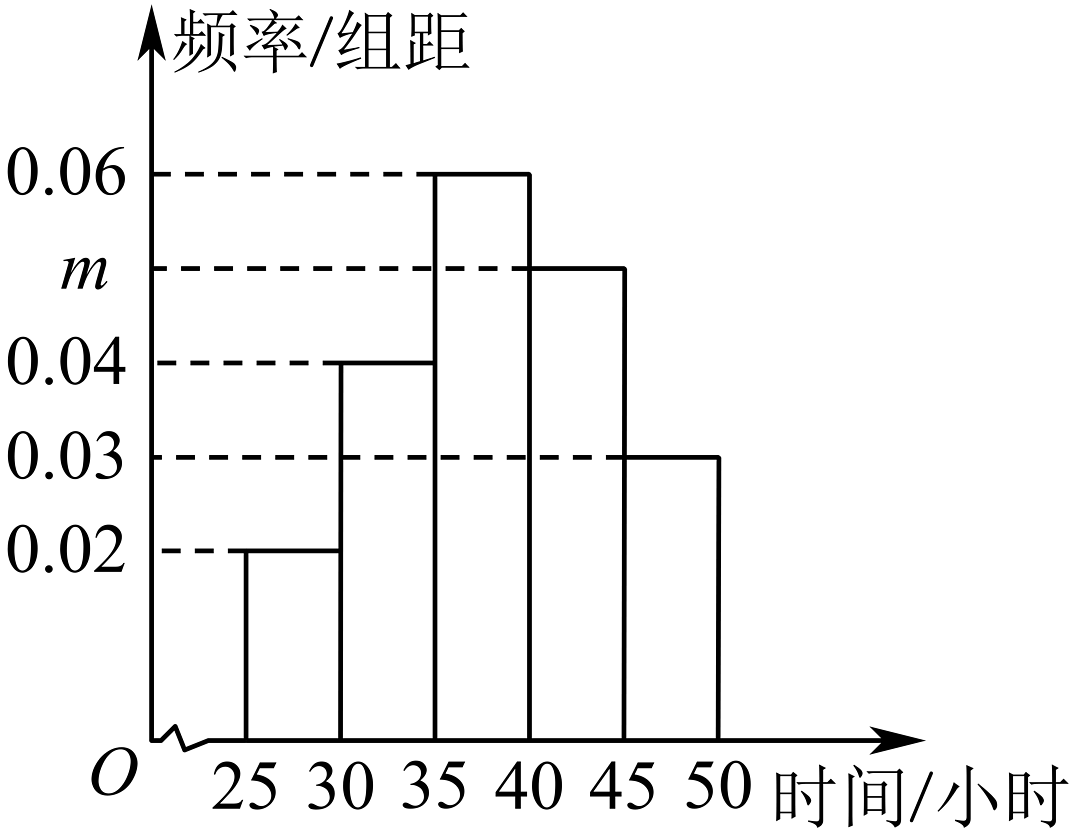 (1)、求的值,并估计该校学生在暑假中参加社区托管活动的时间的平均数(同一组中的数据用该组区间的中点值作代表);(2)、试估计至少参加多少小时的社区托管活动,方可以被评为优秀.
(1)、求的值,并估计该校学生在暑假中参加社区托管活动的时间的平均数(同一组中的数据用该组区间的中点值作代表);(2)、试估计至少参加多少小时的社区托管活动,方可以被评为优秀. -
8、已知一组数据:的平均数为6,则该组数据的分位数为( )A、4.5 B、5 C、5.5 D、6
-
9、函数 , 关于x的方程 , 则下列正确的是( )A、函数的值域为R B、函数的单调减区间为 C、当时,则方程有4个不相等的实数根 D、若方程有3个不相等的实数根,则m的取值范围是
-
10、已知平面向量满足: , 且在上的投影向量为 , 则向量与向量的夹角为( )A、 B、 C、 D、
-
11、已知数列满足 , 且 , 则的通项公式为( )A、 B、 C、 D、
-
12、已知 , , .(1)、求;(2)、若 , 求实数k的值.
-
13、如图,在三棱锥中, , , 分别是侧棱 , , 的中点, , 平面.
 (1)、求证:平面平面;(2)、如果 , , 求二面角的余弦值.
(1)、求证:平面平面;(2)、如果 , , 求二面角的余弦值. -
14、已知向量 , , 若向量在向量上的投影向量 , 则( )A、 B、 C、 D、1
-
15、下列函数的最小值为2的有( )A、 B、 C、 D、
-
16、如图,五面体中, , , 平面ABCD.
 (1)、求证:;(2)、若 , , , 求点E到直线AB的距离;(3)、若 , , , 二面角的余弦值为 , 求DE的长.
(1)、求证:;(2)、若 , , , 求点E到直线AB的距离;(3)、若 , , , 二面角的余弦值为 , 求DE的长. -
17、在高一学生预选科之前,为了帮助他们更好地了解自己是否适合选读物理,我校从高一年级中随机抽取了100名学生的物理成绩,整理得到如图所示的频率分布直方图.
 (1)、求a的值.若根据这次成绩,学校建议的学生选报物理,的学生选报历史,某同学想选报物理,请同他的物理成绩应不低于多少分较为合适?(小数点后保留一位)(2)、这100名学生中,成绩位于内的学生成绩方差为12,成绩位于内的同学成绩方差为10.请估计该年级成绩在80分及以上的学生成绩的方差.(3)、现学校要选拔学生参加物理竞赛,需要再进行考试.考试分为两轮,第一轮需要考2个模块,每个模块成绩从高到低依次有A+,A,B,C,D五个等级,若两个模块成绩均为A+,则直接参加;若一个模块成绩为A+,另一个模块成绩不低于B,则要参加第二轮实验操作,实验操作通过也能参加,否则均不能参加.现有甲、乙二人报名参加,二人互不影响,甲在每个模块考试中取得A+,A,B,C,D的概率分别为;乙在每个模块考试中取得A+,A,B,C,D的概率分别为;甲、乙在实验操作中通过的概率分别为 . 求甲、乙能同时参加物理竞赛的概率.
(1)、求a的值.若根据这次成绩,学校建议的学生选报物理,的学生选报历史,某同学想选报物理,请同他的物理成绩应不低于多少分较为合适?(小数点后保留一位)(2)、这100名学生中,成绩位于内的学生成绩方差为12,成绩位于内的同学成绩方差为10.请估计该年级成绩在80分及以上的学生成绩的方差.(3)、现学校要选拔学生参加物理竞赛,需要再进行考试.考试分为两轮,第一轮需要考2个模块,每个模块成绩从高到低依次有A+,A,B,C,D五个等级,若两个模块成绩均为A+,则直接参加;若一个模块成绩为A+,另一个模块成绩不低于B,则要参加第二轮实验操作,实验操作通过也能参加,否则均不能参加.现有甲、乙二人报名参加,二人互不影响,甲在每个模块考试中取得A+,A,B,C,D的概率分别为;乙在每个模块考试中取得A+,A,B,C,D的概率分别为;甲、乙在实验操作中通过的概率分别为 . 求甲、乙能同时参加物理竞赛的概率. -
18、已知函数 .(1)、求在上的单调递增区间;(2)、已知的内角A,B,C的对边长分别是a,b,c,若 , , 求面积的最大值,及此时a、b的值.
-
19、如图,正四棱柱中, , 点E在上且 .
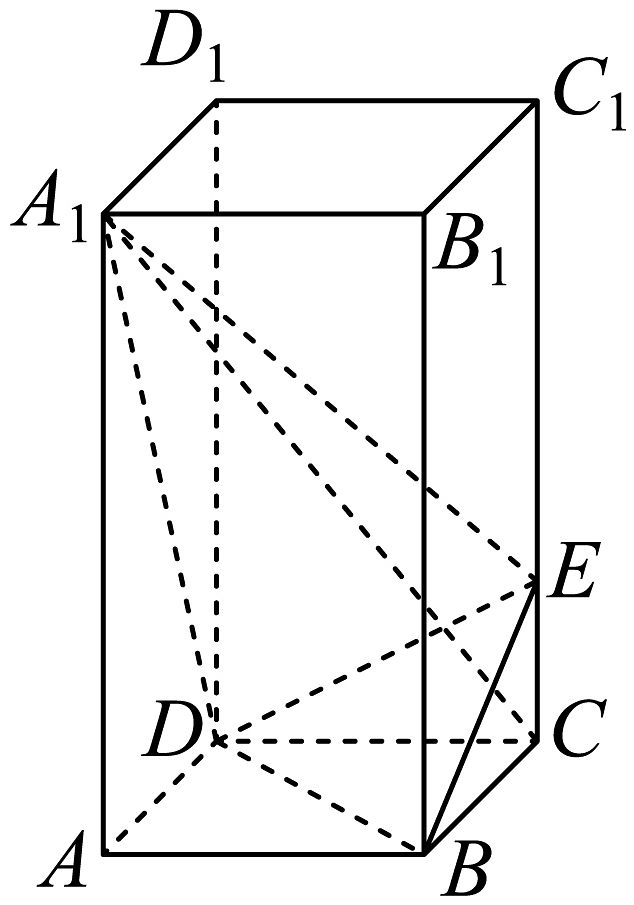 (1)、证明:;(2)、求点B到平面的距离;(3)、求直线与平面所成角的正弦值.
(1)、证明:;(2)、求点B到平面的距离;(3)、求直线与平面所成角的正弦值. -
20、(1)一条光线从点射出,遇反射,反射光线所在直线的倾斜角为 , 若 , 求反射光线所在直线方程;
(2)的三个顶点分别是 , , , 求的外接圆的方程.